本文主要是介绍代码随想录算法训练营第四十九天(动态规划篇)| 474. 一和零, 完全背包理论基础,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
474. 一和零
题目链接:https://leetcode.cn/problems/ones-and-zeroes/submissions/501607337/
思路
之前的背包问题中,我们对背包的限制是容量,即每个背包装的物品的重量和不超过给定容量,这道题的限制是0和1的个数,因此这个背包是二维m和n,最多可以装m个0和n个1。数组中的每个元素都是一个物体,包含若干个0和1。
1. dp数组定义
dp[i][j]: 最多装i个0和j个1的背包最多能装dp[i][j]个物体。
2. 递推公式
遍历每个物体,这个物体有x个0和y个1,我们选择装或者不装这个物体。如果不装它,那么背包中的物体保持原样,如果装它,就要为它腾出相应的0和1的位置,腾出后背包能最多装dp[i-x][j-y]个物体,再加上当前物体,即dp[i-x][j-y]+1,因此递推公式为:
dp[i][j] = max(dp[i][j], dp[i-x][j-y]+1)
3. 初始条件
01背包的dp数组初始化为0就可以。
4. 遍历顺序
外层遍历物体,内层分别遍历背包容量的两个维度,且倒序遍历。在下面的文章中讲过具体细节:代码随想录算法训练营第四十六天(动态规划篇)|01背包(滚动数组方法)-CSDN博客
5. 举例推导dp数组
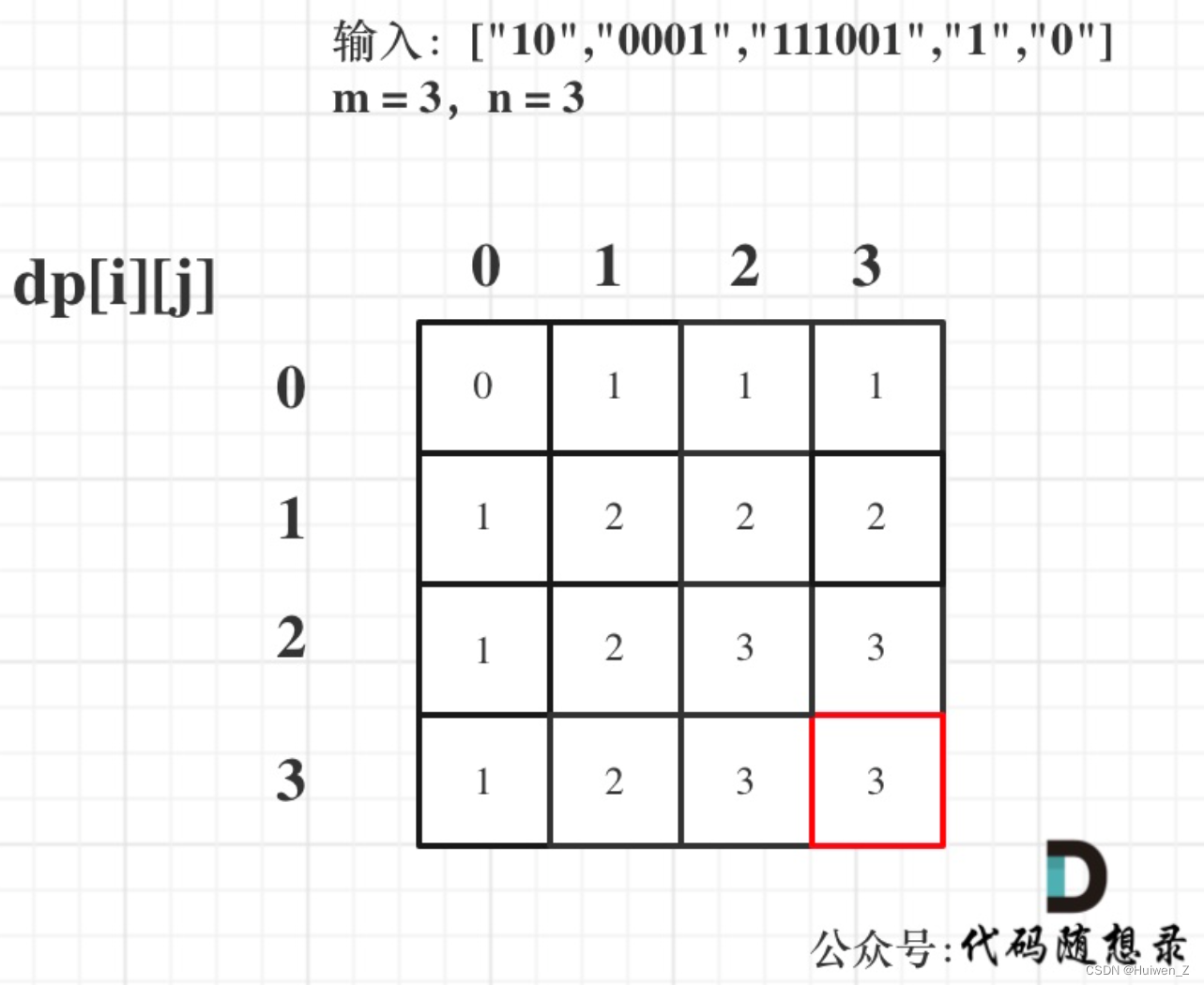
以输入:["10","0001","111001","1","0"],m = 3,n = 3为例
最后dp数组的状态如下所示:
代码实现
class Solution(object):def findMaxForm(self, strs, m, n): # m个0,n个1dp = [[0]*(n+1) for _ in range(m+1)]# zeros, ones = 0, 0for s in strs:zeros = s.count('0')ones = s.count('1')for i in range(m, zeros-1, -1):for j in range(n, ones-1, -1):dp[i][j] = max(dp[i][j], dp[i-zeros][j-ones]+1)return dp[m][n]完全背包理论基础
题目链接:题目页面
思路
完全背包允许物体被重复放入,它的代码与01背包的区别在于遍历顺序。01背包对内部容量的循环是从大到小遍历,为了保证每个物品仅被添加一次。而完全背包的物品是可以添加多次的,所以要从小到大去遍历。
代码实现
N, V = map(int, input().split())
weight, value = [0]*N,[0]*N
for i in range(N):weight[i], value[i] = map(int,input().split())dp = [0]*(V+1)
for i in range(N):for j in range(weight[i], V+1):dp[j] = max(dp[j], dp[j-weight[i]] + value[i])
print(dp[j])
这篇关于代码随想录算法训练营第四十九天(动态规划篇)| 474. 一和零, 完全背包理论基础的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






