本文主要是介绍Catalan数的分析和应用,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
来自:http://blog.csdn.net/dlyme/archive/2008/06/10/2532831.aspx
【Catalan数——卡特兰数】
一.Catalan数的定义令h(1)=1,Catalan数满足递归式:h(n) = h(1)*h(n-1) + h(2)*h(n-2) + ... + h(n-1)h(1),n>=2该递推关系的解为:h(n) = C(2n-2,n-1)/n,n=1,2,3,...(其中C(2n-2,n-1)表示2n-2个中取n-1个的组合数)
二.Catalan数公式推导截图:



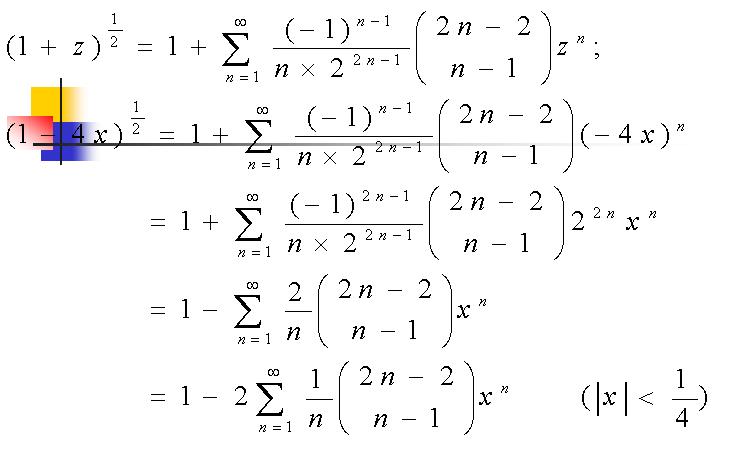

三.Catalan数的典型应用:
1.括号化问题。矩阵链乘: P=A1×A2×A3×……×An,依据乘法结合律,不改变其顺序,只用括号表示成对的乘积,试问有几种括号化的方案?
2.将多边行划分为三角形问题。将一个凸多边形区域分成三角形区域(划分线不交叉)的方法数?
类似:在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?
3.出栈次序问题。一个栈(无穷大)的进栈序列为1,2,3,..n,有多少个不同的出栈序列?
类似:有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票,另外n人只有10元钞票,剧院无其它钞票,问有多少中方法使得只要有10元的人买票,售票处就有5元的钞票找零?(将持5元者到达视作将5元入栈,持10元者到达视作使栈中某5元出栈)
类似:一位大城市的律师在他住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果他从不穿越(但可以碰到)从家到办公室的对角线,那么有多少条可能的道路?
分析:对于每一个数来说,必须进栈一次、出栈一次。我们把进栈设为状态‘1’,出栈设为状态‘0’。n个数的所有状态对应n个1和n个0组成的2n位二进制数。由于等待入栈的操作数按照1‥n的顺序排列、入栈的操作数b大于等于出栈的操作数a(a≤b),因此输出序列的总数目=由左而右扫描由n个1和n个0组成的2n位二进制数,1的累计数不小于0的累计数的方案种数。
在2n位二进制数中填入n个1的方案数为c(2n,n),不填1的其余n位自动填0。从中减去不符合要求(由左而右扫描,0的累计数大于1的累计数)的方案数即为所求。
不符合要求的数的特征是由左而右扫描时,必然在某一奇数位2m+1位上首先出现m+1个0的累计数和m个1的累计数,此后的2(n-m)-1位上有n-m个 1和n-m-1个0。如若把后面这2(n-m)-1位上的0和1互换,使之成为n-m个0和n-m-1个1,结果得1个由n+1个0和n-1个1组成的2n位数,即一个不合要求的数对应于一个由n+1个0和n-1个1组成的排列。
反过来,任何一个由n+1个0和n-1个1组成的2n位二进制数,由于0的个数多2个,2n为偶数,故必在某一个奇数位上出现0的累计数超过1的累计数。同样在后面部分0和1互换,使之成为由n个0和n个1组成的2n位数,即n+1个0和n-1个1组成的2n位数必对应一个不符合要求的数。
因而不合要求的2n位数与n+1个0,n-1个1组成的排列一一对应。
显然,不符合要求的方案数为c(2n,n+1)。由此得出 输出序列的总数目=c(2n,n)-c(2n,n+1)=1/(n+1)*c(2n,n)。(这个公式的下标是从h(0)=1开始的)
这篇关于Catalan数的分析和应用的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







