leetcode-675：为高尔夫比赛砍树 （最短路径算法bfs，dijkstra，A*）

题目

题目连接

你被请来给一个要举办高尔夫比赛的树林砍树。树林由一个 m x n 的矩阵表示， 在这个矩阵中：

0 表示障碍，无法触碰
1 表示地面，可以行走
比 1 大的数 表示有树的单元格，可以行走，数值表示树的高度
每一步，你都可以向上、下、左、右四个方向之一移动一个单位，如果你站的地方有一棵树，那么你可以决定是否要砍倒它。

你需要按照树的高度从低向高砍掉所有的树，每砍过一颗树，该单元格的值变为 1（即变为地面）。

你将从 (0, 0) 点开始工作，返回你砍完所有树需要走的最小步数。 如果你无法砍完所有的树，返回 -1 。

可以保证的是，没有两棵树的高度是相同的，并且你至少需要砍倒一棵树。

示例 1：

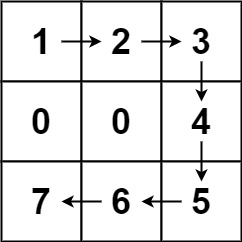
输入：forest = [[1,2,3],[0,0,4],[7,6,5]]
输出：6
解释：沿着上面的路径，你可以用 6 步，按从最矮到最高的顺序砍掉这些树。

示例 2：

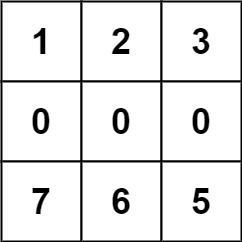
输入：forest = [[1,2,3],[0,0,0],[7,6,5]]
输出：-1
解释：由于中间一行被障碍阻塞，无法访问最下面一行中的树。

示例 3：

输入：forest = [[2,3,4],[0,0,5],[8,7,6]]
输出：6
解释：可以按与示例 1 相同的路径来砍掉所有的树。
(0,0) 位置的树，可以直接砍去，不用算步数。

解题

参考链接

方法一：bfs

可以将树从低到高排序，这样就这样每次要走的，起始点和目的点
然后求起始点和目的点最短路径(bfs)即可
所有最短路径之和就是结果

class Solution {
public:int m,n;vector<vector<int>> dirs={{-1,0},{0,-1},{1,0},{0,1}};int bfs(vector<vector<int>>& forest,int srcx,int srcy,int dstx,int dsty){if(srcx==dstx&&srcy==dsty) return 0;queue<pair<int,int>> q;q.emplace(srcx,srcy);vector<vector<bool>> visited(m,vector<bool>(n,false));visited[srcx][srcy]=true;int depth=0;while(!q.empty()){int l=q.size();while(l--){auto [x,y]=q.front();q.pop();// visited[x][y]=true;//出队的时候才标记，可能会导致重复入队if(x==dstx&&y==dsty){return depth;}for(vector<int>& dir:dirs){int nx=x+dir[0];int ny=y+dir[1];if(nx<0||nx>=m||ny<0||ny>=n||forest[nx][ny]==0||visited[nx][ny]) continue;q.emplace(nx,ny);visited[nx][ny]=true;}}depth++;  }return -1;}int cutOffTree(vector<vector<int>>& forest) {m=forest.size(),n=forest[0].size();vector<pair<int,int>> paths;for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(forest[i][j]>=2){paths.emplace_back(i,j);}}}sort(paths.begin(),paths.end(),[&](pair<int,int>&a,pair<int,int>&b){return forest[a.first][a.second]<forest[b.first][b.second];});int res=0;int srcx=0,srcy=0;for(int i=0;i<paths.size();i++){auto [dstx,dsty]=paths[i];int step=bfs(forest,srcx,srcy,dstx,dsty);if(step==-1) return -1;res+=step;srcx=dstx;srcy=dsty;}return res;}
};

方法二：Dijkstra 算法

也是采用bfs的方法，只不过用【优化队列，每次取出路径最小（把 pair(路径，idx),放入优先队列即可）】的方法， 来取代方法一中的，【层次遍历+每层路径+1】的方法。
在性能上，与方法一来说，其实差不多的

方法三：A* 启发式搜索算法

与Dijstra基本上是一样的，但是 额外记录一个cost，通过优先队列，每次选取cost小的

class Solution {
public:int m,n;int dirs[4][2]={{-1,0},{1,0},{0,-1},{0,1}};int bfs(vector<vector<int>>& forest,int srcx,int srcy,int dstx,int dsty){if(srcx==dstx&&srcy==dsty) return 0;vector<vector<int>> costed(m,vector<int>(n,INT_MAX));costed[srcx][srcy]=abs(dstx-srcx)+abs(dsty-srcy);priority_queue<tuple<int,int,int,int>,vector<tuple<int,int,int,int>>,greater<tuple<int,int,int,int>>> q;q.emplace(costed[srcx][srcy],0,srcx,srcy);while(!q.empty()){auto [cost,dist,x,y]=q.top();q.pop();if(x==dstx&&y==dsty) return dist;for(int i=0;i<4;i++){int nx=x+dirs[i][0];int ny=y+dirs[i][1];if(nx<0||nx>=m||ny<0||ny>=n||forest[nx][ny]==0) continue;int ncost=dist+abs(nx-dstx)+abs(ny-dsty);if(ncost<costed[nx][ny]){q.emplace(ncost,dist+1,nx,ny);costed[nx][ny]=ncost;}}}return -1;}int cutOffTree(vector<vector<int>>& forest) {m=forest.size(),n=forest[0].size();vector<pair<int,int>> paths;for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(forest[i][j]>=2){paths.emplace_back(i,j);}}}sort(paths.begin(),paths.end(),[&](pair<int,int>&a,pair<int,int>&b){return forest[a.first][a.second]<forest[b.first][b.second];});int res=0;int srcx=0,srcy=0;for(int i=0;i<paths.size();i++){auto [dstx,dsty]=paths[i];int step=bfs(forest,srcx,srcy,dstx,dsty);if(step==-1) return -1;res+=step;srcx=dstx;srcy=dsty;}return res;}
};