深度学习图像分类相关概念简析+个人举例1（ANN相关概念与计算）

本文主要是介绍深度学习图像分类相关概念简析+个人举例1（ANN相关概念与计算），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

（1）神经网络：英文全称Artificial Neural Network，简称为ANN。

神经网络是一种模仿人脑神经元结构和功能的人工智能模型。它由多个神经元（也称节点、单元）组成，每个神经元通过计算输入和权重的线性组合，并经过激活函数的非线性转换来产生输出。神经网络可以通过调整权重和偏置来学习输入数据的特征和模式。

以下是神经网络中的一些重要概念和组成部分：

[1] 输入层：接受原始数据输入，将数据传递给网络的下一层。

[2]隐藏层：位于输入层和输出层之间的一层或多层。每个隐藏层由多个神经元组成，对输入数据进行处理和转换。

[3]输出层：产生最终的预测结果或输出，并将结果传递给用户或其他系统。

下面是我画的一个简单的3层2输出的神经网络，三个层级我都标出来了~直接鼠标画的有点粗糙，但是大概就是这个样子的一个神经网络，黑色小圆圈表示神经元哦~

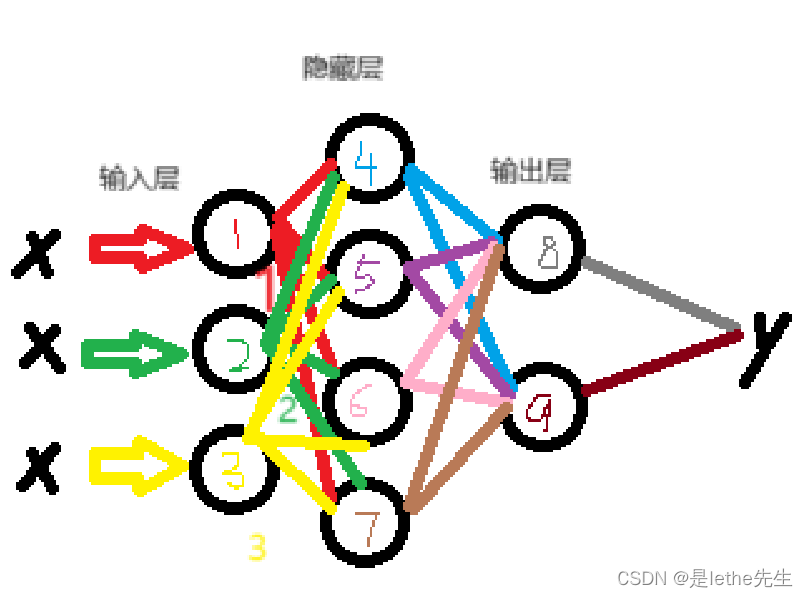
[4]权重（weights）：连接神经元之间的参数，用于调整输入的重要性。

在神经网络中，权重的计算是通过训练过程来自动调整的。具体来说，每个权重与对应的输入相乘，并且所有乘积的总和经过激活函数处理，得到神经网络的输出。

假设我们有上面图中那种的一个简单的神经网络，有一个输入层、一个隐藏层和一个输出层（就上面我画的那种3层的）！！！丑陋但朴实无华嘻嘻~

已知：输入层有3个神经元，隐藏层有4个神经元，输出层有2个神经元。输入1，2，3，这个神经网络具体是怎么运算的？【1】输入层会接收输入信号x：1、2、3，并将它们分别传递到隐藏层的每个神经元（上图的4，5，6，7号神经元）。
【2】假设隐藏层的（4号）第一个神经元的权重分别为w14、w24、w34，（5号）第二个神经元的权重分别为w15、w25、w35，（6号）第三个神经元的权重分别为w16、w26、w36，（7号）第四个神经元的权重分别为w17、w27、w37。此时，隐藏层的每个神经元的输入信号加权求和计算如下：
（图中4号）隐藏层第一个神经元的输入信号加权求和计算为：Z1=w14x1 + w24x2 + w34x3
（图中5号）隐藏层第二个神经元的输入信号加权求和计算为：Z2=w15x1 + w25x2 + w35x3
（图中6号）隐藏层第三个神经元的输入信号加权求和计算为：Z3=w16x1 + w26x2 + w36x3
（图中7号）隐藏层第四个神经元的输入信号加权求和计算为：Z4=w17x1 + w27x2 + w37x3接下来，对隐藏层每个神经元的加权求和结果应用激活函数进行非线性转换。例如，我们使用Sigmoid函数作为激活函数，将其应用于每个神经元的加权求和结果。这样，隐藏层的每个神经元就得到了一个输出结果：

Sigmoid函数的计算公式如下：

$sigmoid(x) = 1 / (1 + exp(-x))$

其中，x是输入的加权求和结果，大白话就是说，对于隐藏层第一个神经元的输入信号加权求和计算为：Z1=w14x1 + w24x2 + w34x3，将该结果Z1作为Sigmoid函数的输入，计算得到隐藏层第一个神经元的输出，a1=sigmoid(z1)= 1 / (1 + exp(-z1))~

隐藏层第一个神经元的输出结果：a1 = sigmoid(z1)
隐藏层第二个神经元的输出结果：a2 = sigmoid(z2)
隐藏层第三个神经元的输出结果：a3 = sigmoid(z3)
隐藏层第四个神经元的输出结果：a4 = sigmoid(z4)

然后隐藏层的输出结果作为权重，分别与输出层的每个神经元相乘，并将乘积求和。

假设输出层的（8号）第一个神经元的权重分别为w41、w51、w61和w71，（9号）第二个神经元的权重分别为w42、w52、w62和w72，以此类推。

此时，输出层的每个神经元的输入信号加权求和计算如下：

输出层第一个神经元的加权求和结果：z5 = w41 * a1 + w51 * a2 + w61 * a3 + w71 * a4
输出层第二个神经元的加权求和结果：z6 = w42 * a1 + w52 * a2 + w62 * a3 + w72 * a4

将输出层的加权求和结果应用于激活函数进行非线性转换。同样地，我们可以使用Sigmoid函数作为激活函数，将其应用于每个神经元的加权求和结果。

这样，输出层的每个神经元就得到了一个输出结果：

输出层第二个神经元的输出结果：a6 = sigmoid(z6)
输出层第一个神经元的输出结果：a5 = sigmoid(z5)

最后，输出层的输出结果a5和a6即为神经网络对于输入1、2、3的运算结果~

[5]偏置（bias）：每个神经元都有一个偏置，用于调整神经元的激活阈值。

偏置（bias）是神经网络中的一个可学习参数，它与每个神经元相连，并且在加权求和的过程中起到偏移输入信号的作用。偏置相当于神经元的阈值，可以影响神经元的激活状态。

以上面提到的神经元模型为例（我画的那个丑图），假设隐藏层的每个神经元都有一个偏置项，分别为b4，b5，b6，b7。那么在计算隐藏层的输入信号加权求和时，会加上对应的偏置项。

隐藏层第一个神经元的输入信号加权求和计算如下：w14x1 + w24x2 + w34x3 + b4
隐藏层第二个神经元的输入信号加权求和计算如下：w15x1 + w25x2 + w35x3 + b5
隐藏层第三个神经元的输入信号加权求和计算如下：w16x1 + w26x2 + w36x3 + b6
隐藏层第四个神经元的输入信号加权求和计算如下：w17x1 + w27x2 + w37x3 + b7

b4，b5，b6，b7分别为隐藏层每个神经元的偏置项。这样，偏置项就可以影响神经元的激活情况。

[6]激活函数（activation function）

就是对神经元的输出进行非线性转换，增加网络的表达能力。常见的激活函数包括Sigmoid、ReLU和tanh等，这里就举Sigmoid函数、ReLU函数和Softmax函数的例子。

（1）Sigmoid函数： Sigmoid函数是一种非线性函数，其公式为： $f(x) = 1 / (1 + e^(-x))$

计算举例：假设输入x = 2，那么根据Sigmoid函数的公式，计算如下： f(2) = 1 / (1 + e^(-2)) ≈ 0.8808

（2）ReLU函数： ReLU函数是一种线性修正函数，其公式为： $f(x) = max(0, x)$

计算举例：假设输入x = -1，根据ReLU函数的公式，计算如下： f(-1) = max(0, -1) = 0

（3）Softmax函数： Softmax函数用于多类别分类问题，将输入信号转换为概率分布。其公式为： $f(x) = e^x / (∑(e^x))$

计算举例：假设输入x = [1, 2, 3]，根据Softmax函数的公式，计算如下： f(x) = [e^1 / (e^1 + e^2 + e^3), e^2 / (e^1 + e^2 + e^3), e^3 / (e^1 + e^2 + e^3)] ≈ [0.0900, 0.2447, 0.6652]

[7]损失函数（loss function）：用于衡量模型在训练过程中的预测与真实值之间的误差。

常见的损失函数包括均方误差（Mean Squared Error，MSE）、交叉熵损失（Cross Entropy Loss）

（1）均方误差（MSE）： MSE损失函数计算预测值与真实值之间的平均平方差。对于单个样本： $MSE(y, y_pred) = (y - y_pred)^2$

计算举例：假设真实值为y = 2，预测值为y_pred = 3，根据MSE损失函数的公式，计算如下： MSE(2, 3) = (2 - 3)^2 = 1

（2）交叉熵损失（Cross Entropy Loss）：交叉熵损失函数常用于分类问题，计算预测结果的概率分布与真实标签的差异。对于二分类问题： $CrossEntropy(y, y_pred) = - (y * log(y_pred) + (1 - y) * log(1 - y_pred))$

计算举例：假设真实标签为y = 1，预测结果的概率分布为y_pred = 0.9，根据交叉熵损失函数的公式，计算如下： CrossEntropy(1, 0.9) = - (1 * log(0.9) + (1 - 1) * log(1 - 0.9)) ≈ 0.1054

[8]反向传播（backpropagation）：通过计算损失函数对权重和偏置的梯度，并使用优化算法进行参数更新，从而训练神经网络。

反向传播（Backpropagation）是一种常用的神经网络训练算法，主要用于计算和更新神经网络中每个连接权重的梯度（即导数）。它利用误差的链式法则，从输出层向输入层反向传播误差信号，根据误差信号更新网络参数。

还是上面那个丑图的结构，我们可以用以下方式表示该神经网络的权重参数：

输入层到隐藏层的权重矩阵：W1（4x3）
隐藏层到输出层的权重矩阵：W2（2x4）

现在，假设我们有一个训练样本，输入值为x，目标输出为y。我们首先将输入x传递给神经网络的输入层，通过隐藏层到输出层进行前向传播，计算得到输出y_hat。然后，我们计算输出误差，即y与y_hat之间的差距。根据误差，我们可以通过反向传播算法来计算每个权重的梯度，并根据梯度更新权重，以使误差最小化。

举例来说，假设我们有一个二分类问题，输出层的激活函数使用sigmoid函数，误差使用平方误差函数。（有空再具体例子整理，会来更新）

输入x为[1, 2, 3]，目标输出y为[0.8, 0.2]。

首先，我们利用前向传播计算输入x通过神经网络得到输出y_hat。这里省略激活函数和偏置项的计算过程。假设经过前向传播，我们得到输出y_hat为[0.6, 0.3]。然后，我们计算输出误差。

平方误差可以表示为：

E = (0.8 - 0.6)^2 + (0.2 - 0.3)^2

接下来，我们根据误差信号，利用反向传播算法计算每个权重的梯度。首先，根据输出误差计算输出层的梯度。对于第i个输出神经元，梯度可以表示为：

delta_output[i] = (y_hat[i] - y[i]) * sigmoid_derivative(y_hat[i])

然后，利用输出层梯度和隐藏层到输出层的权重矩阵W2，计算隐藏层的梯度：

delta_hidden = W2_transpose * delta_output * sigmoid_derivative(hidden_layer_output)

最后，根据隐藏层梯度和输入层到隐藏层的权重矩阵W1，计算输入层的梯度。我们根据梯度和学习率更新权重矩阵W1和W2。例如，更新W1的步骤可以表示为：

W1_new = W1 - learning_rate * delta_hidden * x_transpose

拓展：

神经网络可以具有不同的结构和层级，例如前馈神经网络（Feedforward Neural Network）、递归神经网络（Recurrent Neural Network）和卷积神经网络（Convolutional Neural Network）等。它们在不同领域和任务中具有广泛的应用，如图像识别、语言处理、自然语言处理等。

这篇关于深度学习图像分类相关概念简析+个人举例1（ANN相关概念与计算）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！