C#函数之实现Lagrange插值算法

2024-02-03 03:30
文章标签 c# 算法 实现 函数 .net lagrange 插值 netcore

本文主要是介绍C#函数之实现Lagrange插值算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

博主最近想自己独立地完成一个精密单点定位的应用程序,先实现最简单的功能,那么基础工作就是要对igs最终的精密星历产品进行插值,以满足结算的要求,详细阐述请看前述文章:卫星位置插值方法简介(一)

博主在看过原理后，便使用C#进行了Lagrange函数的编写，话不多说先上代码：

 class interp{public double lagrange(List<double> T, List<double> f,double t){double L = 0;//最后返回的多项式值double[] l = new double[T.Count];//定义的每一个多项式系数列表for (int i = 0; i < l.Length; i++){double l1 = 1;//多项式系数分子double l2 = 1;//多项式系数分母for (int j = 0; j < T.Count; j++){    if (i != j){l1 = l1 * (t - T[j]);l2 = l2 * (T[i] - T[j]);}else{continue;}}l[i] = l1 / l2;}for (int i = 0; i < l.Length; i++){L = L + l[i] * f[i];}return L;}}

首先我是先建立了一个插值函数的类，这里面封装之后会写到的所有的插值函数，包括Lagrange插值和Newton插值法，然后具体实现了Lagrange函数
那么写完之后该怎样调用呢？请先看如下代码：

 public int c;private void comboBox1_SelectedIndexChanged(object sender, EventArgs e){if (comboBox1.Text == "三阶"){c = 1;}if (comboBox1.Text == "五阶"){c = 2;}if (comboBox1.Text == "六阶"){c = 3;}if (comboBox1.Text == "八阶"){c = 4;}if (comboBox1.Text == "十二阶"){c = 5;}}private void button1_Click(object sender, EventArgs e){interp interp = new interp();List<double> T = new List<double>();List<double> ftx = new List<double>();List<double> fty = new List<double>();List<double> ftz = new List<double>();if (c == 1){T.Add(0);T.Add(0.25);T.Add(0.5);T.Add(1);ftx.Add(13686.913694);ftx.Add(14069.247504);ftx.Add(14261.728751);ftx.Add(14209.784087);fty.Add(-22099.331881);fty.Add(-22252.702708);fty.Add(-22148.736352);fty.Add(-21086.622807);ftz.Add(-4728.984963);ftz.Add(-1842.522185);ftz.Add(1076.236929);ftz.Add(6805.670796);double satx = interp.lagrange(T, ftx, 0.75);double saty = interp.lagrange(T, fty, 0.75);double satz = interp.lagrange(T, ftz, 0.75);textBox1.Text = satx.ToString();textBox2.Text = saty.ToString();textBox3.Text = satz.ToString();textBox4.Text = (Convert.ToDouble(textBox1.Text) - 14296.367615).ToString();textBox5.Text = (Convert.ToDouble(textBox2.Text) + 21764.787764).ToString();textBox6.Text = (Convert.ToDouble(textBox3.Text) - 3976.035651).ToString();}if (c == 2){T.Add(0);T.Add(0.25);T.Add(0.5);T.Add(1);T.Add(1.25);T.Add(1.5);ftx.Add(13686.913694);ftx.Add(14069.247504);ftx.Add(14261.728751);ftx.Add(14209.784087);ftx.Add(14041.598305);ftx.Add(13832.692938);fty.Add(-22099.331881);fty.Add(-22252.702708);fty.Add(-22148.736352);fty.Add(-21086.622807);fty.Add(-20109.159114);fty.Add(-18836.848057);ftz.Add(-4728.984963);ftz.Add(-1842.522185);ftz.Add(1076.236929);ftz.Add(6805.670796);ftz.Add(9514.965215);ftz.Add(12055.736360);double satx = interp.lagrange(T, ftx, 0.75);double saty = interp.lagrange(T, fty, 0.75);double satz = interp.lagrange(T, ftz, 0.75);textBox1.Text = satx.ToString();textBox2.Text = saty.ToString();textBox3.Text = satz.ToString();textBox4.Text = (Convert.ToDouble(textBox1.Text) - 14296.367615).ToString();textBox5.Text = (Convert.ToDouble(textBox2.Text) + 21764.787764).ToString();textBox6.Text = (Convert.ToDouble(textBox3.Text) - 3976.035651).ToString();}if (c == 3){T.Add(0);T.Add(0.25);T.Add(0.5);T.Add(1);T.Add(1.25);T.Add(1.5);T.Add(1.75);ftx.Add(13686.913694);ftx.Add(14069.247504);ftx.Add(14261.728751);ftx.Add(14209.784087);ftx.Add(14041.598305);ftx.Add(13832.692938);ftx.Add(13623.421198);fty.Add(-22099.331881);fty.Add(-22252.702708);fty.Add(-22148.736352);fty.Add(-21086.622807);fty.Add(-20109.159114);fty.Add(-18836.848057);fty.Add(-17283.676462);ftz.Add(-4728.984963);ftz.Add(-1842.522185);ftz.Add(1076.236929);ftz.Add(6805.670796);ftz.Add(9514.965215);ftz.Add(12055.736360);ftz.Add(14382.736529);double satx = interp.lagrange(T, ftx, 0.75);double saty = interp.lagrange(T, fty, 0.75);double satz = interp.lagrange(T, ftz, 0.75);textBox1.Text = satx.ToString();textBox2.Text = saty.ToString();textBox3.Text = satz.ToString();textBox4.Text = (Convert.ToDouble(textBox1.Text) - 14296.367615).ToString();textBox5.Text = (Convert.ToDouble(textBox2.Text) + 21764.787764).ToString();textBox6.Text = (Convert.ToDouble(textBox3.Text) - 3976.035651).ToString();}if (c == 4){T.Add(0);T.Add(0.25);T.Add(0.5);T.Add(1);T.Add(1.25);T.Add(1.5);T.Add(1.75);T.Add(2);T.Add(2.25);ftx.Add(13686.913694);ftx.Add(14069.247504);ftx.Add(14261.728751);ftx.Add(14209.784087);ftx.Add(14041.598305);ftx.Add(13832.692938);ftx.Add(13623.421198);ftx.Add(13451.837748);ftx.Add(13352.029724);fty.Add(-22099.331881);fty.Add(-22252.702708);fty.Add(-22148.736352);fty.Add(-21086.622807);fty.Add(-20109.159114);fty.Add(-18836.848057);fty.Add(-17283.676462);fty.Add(-15472.783785);fty.Add(-13435.708124);ftz.Add(-4728.984963);ftz.Add(-1842.522185);ftz.Add(1076.236929);ftz.Add(6805.670796);ftz.Add(9514.965215);ftz.Add(12055.736360);ftz.Add(14382.736529);ftz.Add(16454.540357);ftz.Add(18234.356133);double satx = interp.lagrange(T, ftx, 0.75);double saty = interp.lagrange(T, fty, 0.75);double satz = interp.lagrange(T, ftz, 0.75);textBox1.Text = satx.ToString();textBox2.Text = saty.ToString();textBox3.Text = satz.ToString();textBox4.Text = (Convert.ToDouble(textBox1.Text) - 14296.367615).ToString();textBox5.Text = (Convert.ToDouble(textBox2.Text) + 21764.787764).ToString();textBox6.Text = (Convert.ToDouble(textBox3.Text) - 3976.035651).ToString();}if (c == 5){T.Add(0);T.Add(0.25);T.Add(0.5);T.Add(1);T.Add(1.25);T.Add(1.5);T.Add(1.75);T.Add(2);T.Add(2.25);T.Add(2.5);T.Add(2.75);T.Add(3);T.Add(3.25);ftx.Add(13686.913694);ftx.Add(14069.247504);ftx.Add(14261.728751);ftx.Add(14209.784087);ftx.Add(14041.598305);ftx.Add(13832.692938);ftx.Add(13623.421198);ftx.Add(13451.837748);ftx.Add(13352.029724);ftx.Add(13352.620967);ftx.Add(13475.514776);ftx.Add(13734.929294);ftx.Add(14136.765807);fty.Add(-22099.331881);fty.Add(-22252.702708);fty.Add(-22148.736352);fty.Add(-21086.622807);fty.Add(-20109.159114);fty.Add(-18836.848057);fty.Add(-17283.676462);fty.Add(-15472.783785);fty.Add(-13435.708124);fty.Add(-11211.291704);fty.Add(-8844.292298);fty.Add(-6383.760457);fty.Add(-3881.252747);ftz.Add(-4728.984963);ftz.Add(-1842.522185);ftz.Add(1076.236929);ftz.Add(6805.670796);ftz.Add(9514.965215);ftz.Add(12055.736360);ftz.Add(14382.736529);ftz.Add(16454.540357);ftz.Add(18234.356133);ftz.Add(19690.739661);ftz.Add(20798.192448);ftz.Add(21537.629852);ftz.Add(21896.709250);double satx = interp.lagrange(T, ftx, 0.75);double saty = interp.lagrange(T, fty, 0.75);double satz = interp.lagrange(T, ftz, 0.75);textBox1.Text = satx.ToString();textBox2.Text = saty.ToString();textBox3.Text = satz.ToString();textBox4.Text = (Convert.ToDouble(textBox1.Text) - 14296.367615).ToString();textBox5.Text = (Convert.ToDouble(textBox2.Text) + 21764.787764).ToString();textBox6.Text = (Convert.ToDouble(textBox3.Text) - 3976.035651).ToString();}}

首先说明一下，本次编写只为完成基本功能，因此已知数值等信息是直接传入到列表中。
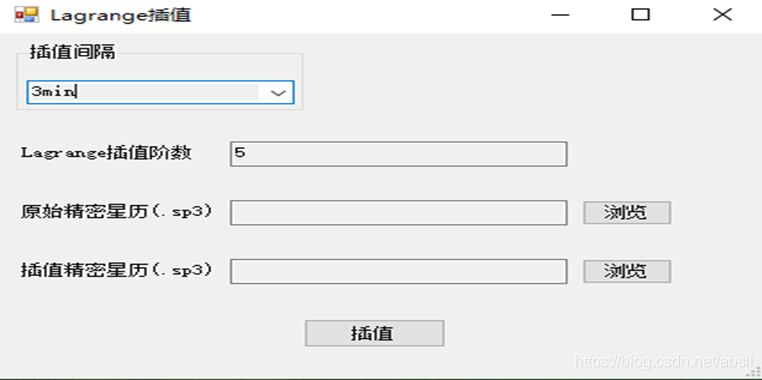
下面展示一下程序具体界面：
在这里插入图片描述三阶（x,y米级，z厘米级）

在这里插入图片描述五阶（x毫米级,y 厘米级，z亚毫米级）

在这里插入图片描述六阶（x毫米级,y 亚毫米级，z亚毫米级）
在这里插入图片描述八阶（x米级,y 米级，z米级）
在这里插入图片描述
十二阶（x米级,y 米级，z米级）
我们可以看到，插值精度并不会随着插值阶数的不断增加而不断提高，到达一定阶数后，精度反而会降低，产生龙格现象。

以上就是C#实现Lagrange插值算法的全部内容啦！

博主后面会将整个精密星历文件都进行Lagrange插值，并输出为.sp3文件，敬请期待哦！
在这里插入图片描述

感谢关注！感谢支持！一起学习，一起进步！文中若有疏漏之处，还请指正！

这篇关于C#函数之实现Lagrange插值算法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/672865。

相关文章

C# 比较两个list 之间元素差异的常用方法

C# 比较两个list 之间元素差异的常用方法

《C#比较两个list之间元素差异的常用方法》：本文主要介绍C#比较两个list之间元素差异,本文通过实例代码给大家介绍的非常详细,对大家的学习或工作具有一定的参考借鉴价值,需要的朋友参考下吧... 目录1. 使用Except方法2. 使用Except的逆操作3. 使用LINQ的Join,GroupJoin
阅读更多...
Python函数作用域示例详解

Python函数作用域示例详解

《Python函数作用域示例详解》本文介绍了Python中的LEGB作用域规则,详细解析了变量查找的四个层级,通过具体代码示例,展示了各层级的变量访问规则和特性,对python函数作用域相关知识感兴趣... 目录一、LEGB 规则二、作用域实例2.1 局部作用域（Local）2.2 闭包作用域（Enclos
阅读更多...
Python实现对阿里云OSS对象存储的操作详解

Python实现对阿里云OSS对象存储的操作详解

《Python实现对阿里云OSS对象存储的操作详解》这篇文章主要为大家详细介绍了Python实现对阿里云OSS对象存储的操作相关知识,包括连接,上传,下载,列举等功能,感兴趣的小伙伴可以了解下... 目录一、直接使用代码二、详细使用1. 环境准备2. 初始化配置3. bucket配置创建4. 文件上传到os
阅读更多...
关于集合与数组转换实现方法

关于集合与数组转换实现方法

《关于集合与数组转换实现方法》：本文主要介绍关于集合与数组转换实现方法,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录1、Arrays.asList()1.1、方法作用1.2、内部实现1.3、修改元素的影响1.4、注意事项2、list.toArray()2.1、方
阅读更多...
Java中的雪花算法Snowflake解析与实践技巧

Java中的雪花算法Snowflake解析与实践技巧

《Java中的雪花算法Snowflake解析与实践技巧》本文解析了雪花算法的原理、Java实现及生产实践,涵盖ID结构、位运算技巧、时钟回拨处理、WorkerId分配等关键点,并探讨了百度UidGen... 目录一、雪花算法核心原理1.1 算法起源1.2 ID结构详解1.3 核心特性二、Java实现解析2.
阅读更多...
使用Python实现可恢复式多线程下载器

使用Python实现可恢复式多线程下载器

《使用Python实现可恢复式多线程下载器》在数字时代,大文件下载已成为日常操作,本文将手把手教你用Python打造专业级下载器,实现断点续传,多线程加速,速度限制等功能,感兴趣的小伙伴可以了解下... 目录一、智能续传：从崩溃边缘抢救进度二、多线程加速：榨干网络带宽三、速度控制：做网络的好邻居四、终端交互
阅读更多...
MySQL count()聚合函数详解

MySQL count()聚合函数详解

《MySQLcount()聚合函数详解》MySQL中的COUNT()函数,它是SQL中最常用的聚合函数之一,用于计算表中符合特定条件的行数,本文给大家介绍MySQLcount()聚合函数,感兴趣的朋... 目录核心功能语法形式重要特性与行为如何选择使用哪种形式？总结深入剖析一下 mysql 中的 COUNT
阅读更多...
java实现docker镜像上传到harbor仓库的方式

java实现docker镜像上传到harbor仓库的方式

《java实现docker镜像上传到harbor仓库的方式》：本文主要介绍java实现docker镜像上传到harbor仓库的方式,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地... 目录1. 前 言2. 编写工具类2.1 引入依赖包2.2 使用当前服务器的docker环境推送镜像2.2
阅读更多...
C++20管道运算符的实现示例

C++20管道运算符的实现示例

《C++20管道运算符的实现示例》本文简要介绍C++20管道运算符的使用与实现,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小编来一起学习学习吧... 目录标准库的管道运算符使用自己实现类似的管道运算符我们不打算介绍太多，因为它实际属于c++20最为重要的
阅读更多...
Java easyExcel实现导入多sheet的Excel

Java easyExcel实现导入多sheet的Excel

《JavaeasyExcel实现导入多sheet的Excel》这篇文章主要为大家详细介绍了如何使用JavaeasyExcel实现导入多sheet的Excel,文中的示例代码讲解详细,感兴趣的小伙伴可... 目录1.官网2.Excel样式3.代码1.官网easyExcel官网2.Excel样式3.代码
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2