【聚类】|多维尺度分析 MDS

ref
https://blog.csdn.net/Dark_Scope/article/details/53229427

1 目的

已知很多样本点之间的相互距离（以欧式距离为例），但是不知道每个样本点的具体坐标，MDS分析就是要求解出每个样本点的原始坐标，然后保证这些样本点的原始坐标尽量符合这个距离矩阵关系。

MDS利用的是成对样本间相似性，目的是利用这个信息去构建合适的低维空间，是的样本在此空间的距离和在高维空间中的样本间的相似性尽可能的保持一致。

如
已知几大城市之间的距离，但是不知道他们的经纬度，现在要求他们之间的相对位置关系。

计算步骤

1）从距离矩阵D中，求解出B。

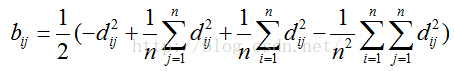
其中，B的含义如下式：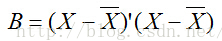
X代表每个数据的原始坐标，在本例中，X也就代表这些城市的坐标信息。

公式2与公式1是可以相互推导的。

接下来的分析就跟PCA有点相似了。我们知道在PCA中，也是首先求出原始数据的协方差矩阵，然后再计算协方差矩阵的前n个特征值对应的特征向量，就是原始样本点的几个重要的方向。

（2）计算B的特征值与特征向量，找到前n个值对应的特征向量。用这些特征值特征向量把B对角化

B = F’ A F

其中A是以前n个特征值为对角线元素的对角阵，F是特征向量组成的矩阵。

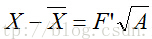
然后就可以画出来相对位置了。在选择前n个特征值的时候，如果选择1个，那么会得到他们之间的1维关系，如果n = 2，那么会得到他们之间的二维关系。

import numpy as np
import matplotlib.pyplot as pltdef mds(D,q):D = np.asarray(D)DSquare = D**2totalMean = np.mean(DSquare)columnMean = np.mean(DSquare, axis = 0)rowMean = np.mean(DSquare, axis = 1)B = np.zeros(DSquare.shape)for i in range(B.shape[0]):for j in range(B.shape[1]):B[i][j] = -0.5*(DSquare[i][j] - rowMean[i] - columnMean[j]+totalMean)eigVal,eigVec = np.linalg.eig(B)X = np.dot(eigVec[:,:q],np.sqrt(np.diag(eigVal[:q])))return XD = [[0,587,1212,701,1936,604,748,2139,2182,543],
[587,0,920,940,1745,1188,713,1858,1737,597],
[1212,920,0,879,831,1726,1631,949,1021,1494],
[701,940,879,0,1374,968,1420,1645,1891,1220],
[1936,1745,831,1374,0,2339,2451,347,959,2300],
[604,1188,1726,968,2339,0,1092,2594,2734,923],
[748,713,1631,1420,2451,1092,0,2571,2408,205],
[2139,1858,949,1645,347,2594,2571,0,678,2442],
[2182,1737,1021,1891,959,2734,2408,678,0,2329],
[543,597,1494,1220,2300,923,205,2442,2329,0]]label = ['Atlanta','Chicago','Denver','Houston','Los Angeles','Miami','New York','San Francisco','Seattle','Washington, DC']
X = mds(D,2)
plt.plot(X[:,0],X[:,1],'o')
for i in range(X.shape[0]):plt.text(X[i,0]+25,X[i,1]-15,label[i])
plt.show()