深度通信网络专栏（4）|自编码器：Blind Channel Equalization using Variational Autoencoders

本文地址：https://arxiv.org/abs/1803.01526

前言

深度通信网络专栏|自编码器:整理2018-2019年使用神经网络实现通信系统自编码器的论文，一点拙见，如有偏颇，望不吝赐教，顺颂时祺。

文章主要贡献

原来提出的最大似然估计下的盲信道均衡使用期望最大或近似期望最大，计算复杂度过高。

本文提出用变分自编码器（VAE）实现最大似然估计下的盲信道均衡，与恒模算法（CMA）相比可达到更低的ber和更低的信道获取时延。VAE的性能接近非盲自适应线性最小均方误差均衡器。

VAE由两层卷积层和少量自由参数构成，虽然计算复杂度比CMA高，但是需要估计的自由参数个数较少。

系统模型

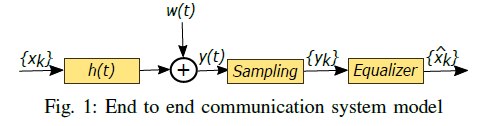
一个端到端系统可表示为以上结构，$\mathbf{y}=\mathbf{x}\ast \mathbf{h}+\mathbf{w}$
使用QPSK调制，则$\mathrm{x}={\mathrm{x}}^I+j\cdot {\mathrm{x}}^Q$，$\mathbf{h}={\mathbf{h}}^I+j\cdot {\mathbf{h}}^Q$，$\mathbf{y}={\mathbf{y}}^I+j\cdot {\mathbf{y}}^Q$
给定x，y 的条件概率函数为：
$\begin{array}{rl}{p}_{\mathbf{\theta }}(\mathbf{y}|\mathbf{x})& =p_{\mathbf{\theta }}\left({\mathbf{y}}^I|{\mathbf{x}}^I\right)p_{\mathbf{\theta }}\left({\mathbf{y}}^Q|{\mathbf{x}}^Q\right)\\ & =\frac{1}{{\left(\pi {\sigma }_w^2\right)}^N}\cdot e^{-\Vert \mathbf{y}-\mathbf{x}\ast \mathbf{h}{\Vert }^2/{\sigma }_w^2}\end{array}$

变分自编码器

ML估计，即是估计向量h 和噪声方差${\sigma }_w^2$，使得$\log p_{\mathbf{\theta }}(\mathbf{y})$最大，令$\mathbf{\theta }\triangleq \left\{\mathbf{h},{\sigma }_w^2\right\}$。使用变分法可以简化这一信道估计问题：使用变分法求泛函数$\log p_{\mathbf{\theta }}(\mathbf{y})$的极小值，将问题转化为 最大化$\log p_{\mathbf{\theta }}(\mathbf{y})$的lower bound！使用神经网络解决此最大最小化问题。

补充：变分法
- 变分法用于求解使泛函数取得极大值或极小值的极值函数 。
- 泛函数：输入是一个函数，输出是一个值。
- 通常在变分法中，泛函数是一个积分
eg. $I(y)={\int }_{x_1}^{x_2}Fdx$,F可以是y(x)和y(x)各阶导数的函数。
- 在这里$p_{\mathbf{\theta }}(\mathbf{y})={\int }_{\mathbf{x}}p(\mathbf{x})p_{\mathbf{\theta }}(\mathbf{y}|\mathbf{x})d\mathbf{x}$ ，y是x的函数。

$$\begin{array}{rl}\log p_{\mathbf{\theta }}(\mathbf{y})\ge & {\mathbb{E}}_{q_{\Phi }(\mathbf{x}|\mathbf{y})}\left[-\log q_{\Phi }(\mathbf{x}|\mathbf{y})+\log p_{\mathbf{\theta }}(\mathbf{x},\mathbf{y})\right]\\ =& \underset{A}{\underbrace{-D_{KL}\left[q_{\Phi }(\mathbf{x}|\mathbf{y})\Vert p(\mathbf{x})\right]}}\\ & +\underset{B}{\underbrace{{\mathbb{E}}_{q_{\Phi }(\mathbf{x}|\mathbf{y})}\left[\log p_{\mathbf{\theta }}(\mathbf{y}|\mathbf{x})\right]}}\triangleq -\mathcal{L}(\mathbf{\theta },\mathbf{\Phi },\mathbf{y})\end{array}$$
引入了自由参数Φ，问题转化为找到θ和Φ，使得$\mathcal{L}(\mathbf{\theta },\mathbf{\Phi },\mathbf{y})$最小。那么如何得到$\mathcal{L}(\mathbf{\theta },\mathbf{\Phi },\mathbf{y})$呢？
分析上式，可知上式与$p_{\mathbf{\theta }}(\mathbf{y}|\mathbf{x})$，$q_{\Phi }(\mathrm{x}|\mathrm{y})$，$p(\mathbf{x})$有关，其中：$$\begin{array}{rl}{p}_{\mathbf{\theta }}(\mathbf{y}|\mathbf{x})& =p_{\mathbf{\theta }}\left({\mathbf{y}}^I|{\mathbf{x}}^I\right)p_{\mathbf{\theta }}\left({\mathbf{y}}^Q|{\mathbf{x}}^Q\right)\\ & =\frac{1}{{\left(\pi {\sigma }_w^2\right)}^N}\cdot e^{-\Vert \mathbf{y}-\mathbf{x}\ast \mathbf{h}{\Vert }^2/{\sigma }_w^2}\end{array}$$
$$p(\mathbf{x})=p\left({\mathbf{x}}^I\right)p\left({\mathbf{x}}^Q\right)=2^{-2N}$$
只需得到$q_{\Phi }(\mathrm{x}|\mathrm{y})$即可得到$\mathcal{L}(\mathbf{\theta },\mathbf{\Phi },\mathbf{y})$，此时可用解析的方法找到θ和Φ。

引入神经网络

用神经网络来求$q_{\Phi }(\mathrm{x}|\mathrm{y})$：$$q_{\Phi }(\mathrm{x}|\mathrm{y})=\prod _{j=0}^{N-1}{q}_{\Phi }\left(x_j|\mathrm{y}\right)=\prod _{j=0}^{N-1}{q}_{\Phi }\left(x_j^I|\mathrm{y}\right)q_{\Phi }\left(x_j^Q|\mathrm{y}\right)$$
神经网络的输出为$q_{\Phi }\left(x_j^I|\mathbf{y}\right)和q_{\Phi }\left(x_j^Q|\mathbf{y}\right)$，输出维度为2N.

至此，我们得到了$\mathcal{L}(\mathbf{\theta },\mathbf{\Phi },\mathbf{y})$的显示表达。

仿真结果