本文主要是介绍球面谐波函数 (Spherical harmonic function)分析实际颗粒形状公式推导及数值实现 Part 1,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、公式推导
球面谐波函数是一组定义在单位球上的基函数,是傅里叶展开式的一种;球面谐波函数最早应用于电磁场、核物理学、行星重力场计算,Garboczi (2002)最早基于该方法分析了混凝土集料的颗粒形状特性;展现出其对颗粒形状解析表征的强大能力。
球面谐波函数对颗粒形状分析主要原理是将颗粒的形状视作一个三维的解析表达式,并能够用球面谐波基函数的线性组合进行展开,如下式表示:
其中,表示阶数,
表示次数;
表示球面谐波基函数,表达式如下:
表示关联勒让德函数,系数的表达式如下:
其中星号表示共轭复数。以上是Garboczi在该方法的原始文献中提出的系数求解方法;后续的研究对此求解方法进行了改进(Zhou Bo等, 2015,香港城市大学),的表达式可以写成:
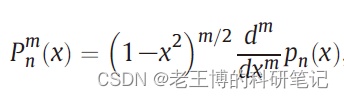
其中,表达式如下:

接下来是系数的计算,将要分析的颗粒的表面进行参数化,映射到一个单位球体中(接下来的文章中再介绍),坐标用表示,如下:
![]()
那么根据第一个式子,我们就能得到一个线性方程组,注意这个方程组中是将转化成一个行向量,依次计算(m,n)为(0,0)、(-1,1)、(0,1) ......时候的值,如下所示:
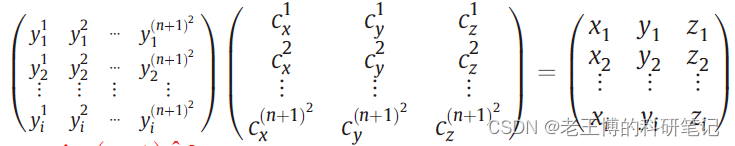
这样只要选的原始颗粒上的坐标个数足够多大于
,就能得到确定的系数值。
二、球面谐波基函数 的数值实现
的数值实现
数值实现时,一般采用分段的形式将球面谐波函数写出:
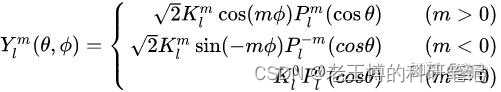

时候,
等于:

在Matlab中编程实现(实数形式的基函数),程序及注释如下:
% 定义参数l = 3; % 角动量量子数m = -3; % 磁量子数% 创建球坐标网格theta = linspace(0, pi, 100);phi = linspace(0, 2*pi, 200);[Theta, Phi] = meshgrid(theta, phi);if l ~= 0% 计算KlmKlm = sqrt((2 * l + 1) * factorial(l - abs(m)) / (4 * pi * factorial(l + abs(m))));if m > 0% 计算勒让德多项式Plm1 = legendre(l,cos(Theta));Plm = reshape(Plm1(m + 1,:,:), size(Phi));Ylm = sqrt(2) .* Klm .* cos(m .* Phi) .* Plm;endif m < 0Plm1 = legendre(l,cos(Theta));Plm = reshape(Plm1(- m + 1,:,:), size(Phi));Ylm = sqrt(2) .* Klm .* sin(- m .* Phi) .* Plm;endif m == 0Klm = sqrt((2 * l + 1) * factorial(l - abs(m)) / (4 * pi * factorial(l + abs(m))));Plm1 = legendre(l,cos(Theta));Plm = reshape(Plm1(m + 1,:,:), size(Phi));Ylm = Klm .* Plm;end% 可视化R = abs(Ylm); % 球面谐波函数的幅度X = R .* sin(Theta) .* cos(Phi);Y = R .* sin(Theta) .* sin(Phi);Z = R .* cos(Theta);figure;surf(X, Y, Z, real(Ylm),'EdgeColor','none'); % 使用实部作为颜色映射title(['球面谐波函数 Y_', num2str(l), '^', num2str(m)]);xlabel('X');ylabel('Y');zlabel('Z');colormap('jet')colorbar;axis equal;elseYlm = 0.5 * sqrt(1 / pi);% 可视化R = abs(Ylm); % 球面谐波函数的幅度X = R .* sin(Theta) .* cos(Phi);Y = R .* sin(Theta) .* sin(Phi);Z = R .* cos(Theta);figure;surf(X, Y, Z,'EdgeColor','none'); % 使用实部作为颜色映射title(['球面谐波函数 Y_', num2str(l), '^', num2str(m)]);xlabel('X');ylabel('Y');zlabel('Z');colormap('jet')colorbar;axis equal;end运行结果:
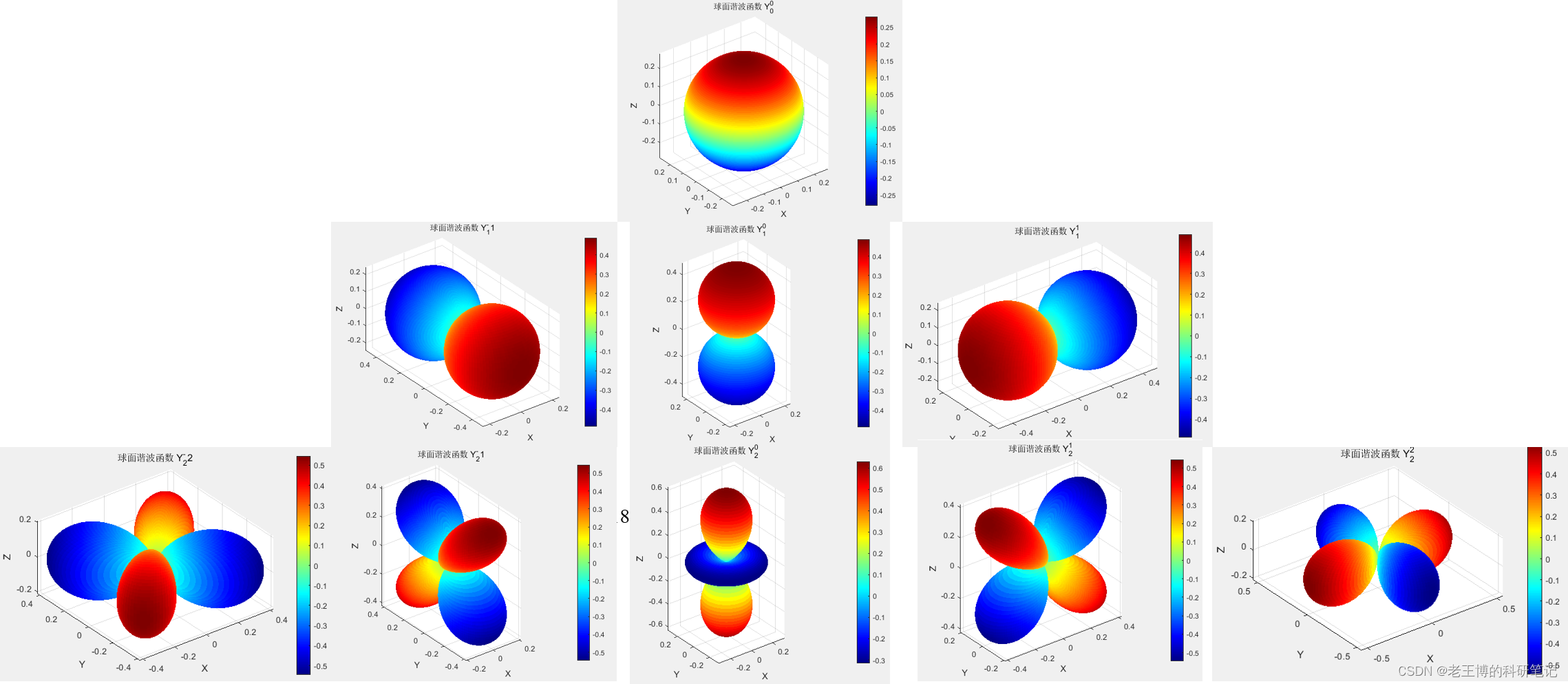
相关的Python程序链接:
https://scipython.com/blog/visualizing-the-real-forms-of-the-spherical-harmonics/
理论链接:
https://mrtrix.readthedocs.io/en/latest/concepts/spherical_harmonics.html
这篇关于球面谐波函数 (Spherical harmonic function)分析实际颗粒形状公式推导及数值实现 Part 1的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






