基于Tent映射的自适应鲸鱼优化算法

本文主要是介绍基于Tent映射的自适应鲸鱼优化算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

一、理论基础
- 1、标准鲸鱼优化算法(WOA)
- 2、改进鲸鱼优化算法(IWOA)
- - （1）Tent映射
  - （2）引入自适应权重
  - （3）自适应阈值
  - （4）IWOA算法步骤
二、函数测试与结果分析
三、参考文献

一、理论基础

1、标准鲸鱼优化算法(WOA)

请参考这里。

2、改进鲸鱼优化算法(IWOA)

（1）Tent映射

混沌具有随机性和遍历性和初值敏感性，能使算法有更快的收敛速度。本文采用Tent映射来产生混沌序列，对种群进行初始化，使得初始解尽可能均匀的分布在解空间内。 $z_{k+1}=\begin{dcases}2z_k,\quad\quad\,\,\,\quad 0≤z_≤0.5\\2(1-z_k),\quad 0.5<z_k≤1\end{dcases}\tag{1}$ 其中， $k$ 表示映射次数， $z_k$ 表示第 $k$ 次映射函数值。
经过伯努利移位变换后表示如下： $x_{n+1}=(2x_n)\text{mod}\,1\tag{2}$

（2）引入自适应权重

本文把惯性权重引入WOA中，作用于包围猎物和螺旋更新机制的位置更新中，权值 $w$ 随之迭代次数的增加而非线性递减，当算法在初期时的权重系数比较大时，此时具有较强的全局搜索能力，随着迭代次数的增加，权重系数在减小，算法可以在某一区域内进行精细搜索，防止陷入局部最优，提高求解的精度，鲸鱼位置更新公式如下： $X(t+1)=wX^*(t)-A\cdot D\tag{3}$ $X(t+1)=D'\cdot e^{bl}\cdot\cos(2\pi l)+wX^*(t)\tag{4}$ 其中： $w(t)=e^{-\left(\frac{t}{Max\_iter}\right)^k}\tag{5}$ 其中， $t$ 为当前迭代次数， $Max\_iter$ 是最大迭代次数， $k$ 是调节系数，调节权重的大小。调节系数取不一样值权重变化如图1所示。
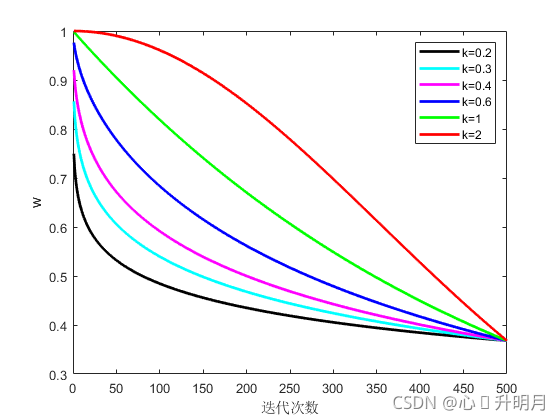
在这里插入图片描述

图1 权重变化曲线
本文取

k = 0.4

，来平衡鲸鱼优化算法的全局和局部搜索能力。

（3）自适应阈值

标准鲸鱼优化算法设置概率阈值为0.5，来同步包围和螺旋过程。通过随机生成的 $p$ 值与概率阈值来选择不同的狩猎策略。但是随着迭代次数的增加，这种方式的捕食方式会导致算法陷入局部最优等问题，因此本文提出一个对数形式的自适应概率阈值 $p^{'}$ 来平衡全局搜索和局部开发的能力，表达式如下： $p'=1-\log_{10}\left(1+\frac{9t}{Max\_iter}\right)\tag{6}$

（4）IWOA算法步骤

综上，本文提出的改进的鲸鱼优化算法的主要步骤如下：
步骤1：初始化鲸鱼算法基本参数，种群规模 $N$ ，最大迭代次数 $Max\_iter$ ，问题维数 $D$ ，对数螺线形状参数 $b$ ；
步骤2：利用Tent混沌映射初始化鲸鱼位置；
步骤3：对目标函数进行求解，计算每个搜索个体的适应度，找到当前最优解；
步骤4：若 $p < p^{'}$ 且 $∣ A ∣ < 1$ ，按式(3)进行更新；
步骤5：若 $p < p^{'}$ 且 $∣ A ∣ \geq 1$ ，按WOA对应公式进行螺旋运动的方式向猎物进行更新；
步骤6：若 $p \geq p^{'}$ ，按式(4)进行全局搜索；
步骤7：位置更新完毕，计算每个个体的适应度值，与先前的最佳搜索代理位置进行比较，若优于 $X^*$ ，则替换 $X^*$ ；
步骤8：判断是否达到最大迭代次数，若满足则终止迭代，同时输出最优解和适应度值，反之返回步骤4。

二、函数测试与结果分析

为验证改进鲸鱼优化算法的有效性，选用标准鲸鱼优化算法(WOA)、灰狼优化算法(GWO和粒子群优化算法(PSO)和其进行对比，算法参数设置如文献[1]中表1所示。设置种群规模为30，最大迭代次数为500，每个算法独立运算20次，以文献[1]中表2的6个30维的测试函数为例。结果显示如下：
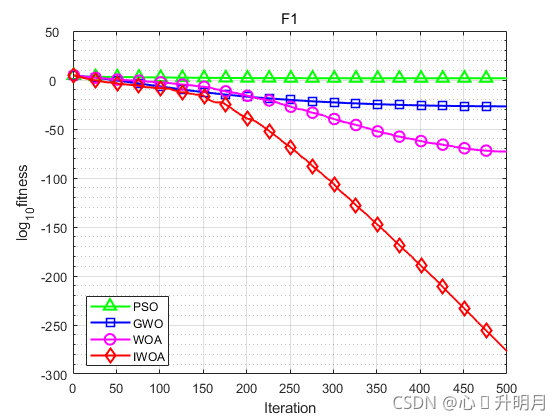
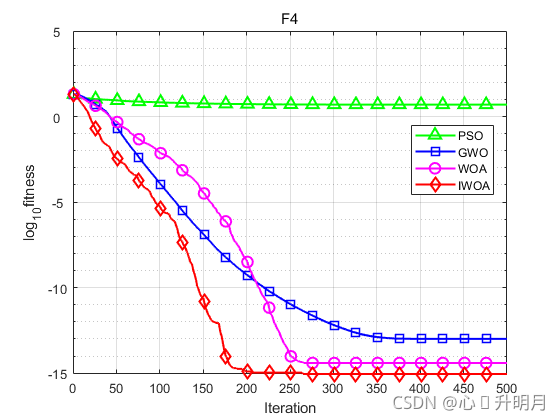
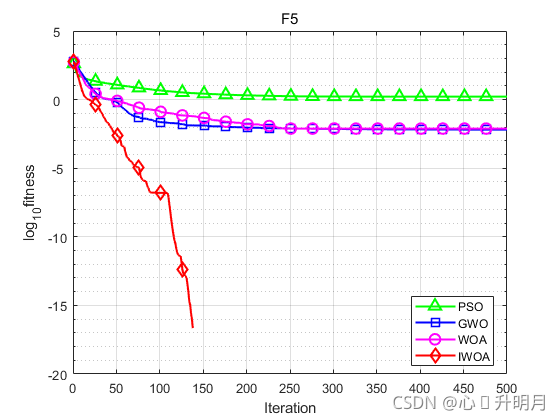
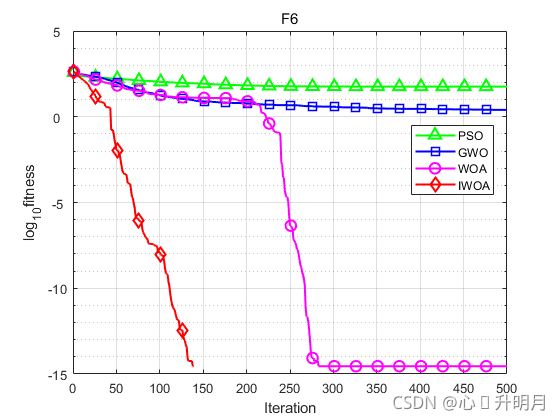
在这里插入图片描述

函数：F1
PSO：最差值: 147.8448,最优值:23.4933,平均值:63.9767,标准差:32.1388,秩和检验:6.7956e-08
GWO：最差值: 1.7889e-26,最优值:7.1869e-29,平均值:1.36e-27,标准差:3.9183e-27,秩和检验:6.7956e-08
WOA：最差值: 1.0992e-72,最优值:2.7991e-84,平均值:9.2059e-74,标准差:2.8764e-73,秩和检验:6.7956e-08
IWOA：最差值: 3.6756e-276,最优值:9.4649e-296,平均值:1.8382e-277,标准差:0,秩和检验:1
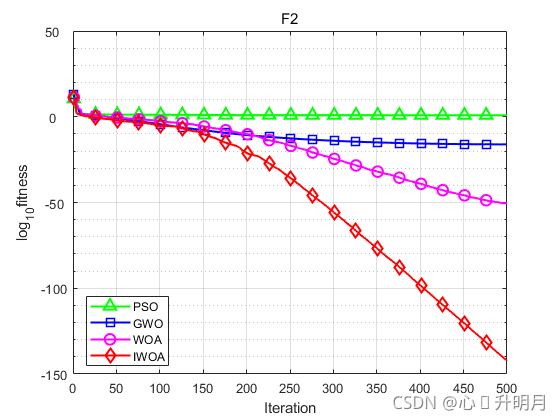
函数：F2
PSO：最差值: 13.6415,最优值:3.7539,平均值:8.1522,标准差:2.8786,秩和检验:6.7956e-08
GWO：最差值: 3.699e-16,最优值:7.9544e-18,平均值:8.2037e-17,标准差:8.5695e-17,秩和检验:6.7956e-08
WOA：最差值: 6.4078e-50,最优值:1.1677e-60,平均值:3.5018e-51,标准差:1.4268e-50,秩和检验:6.7956e-08
IWOA：最差值: 9.864e-142,最优值:6.1064e-152,平均值:5.4801e-143,标准差:2.2039e-142,秩和检验:1
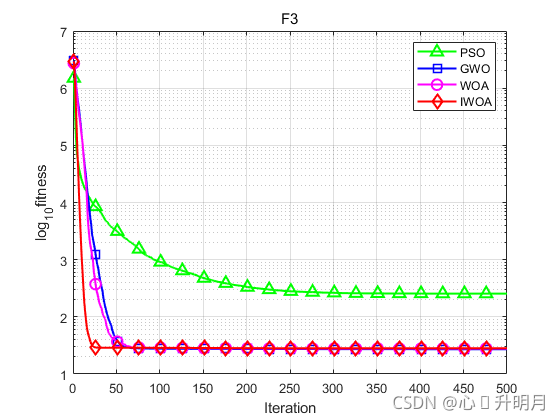
函数：F3
PSO：最差值: 632.6858,最优值:100.3085,平均值:254.1884,标准差:144.4872,秩和检验:6.7956e-08
GWO：最差值: 28.7687,最优值:25.8787,平均值:27.0773,标准差:0.90809,秩和检验:1.8074e-05
WOA：最差值: 28.7457,最优值:27.1368,平均值:27.8405,标准差:0.4534,秩和检验:0.00083572
IWOA：最差值: 28.626,最优值:27.9667,平均值:28.2328,标准差:0.18107,秩和检验:1
函数：F4
PSO：最差值: 5.9211,最优值:3.6118,平均值:4.9672,标准差:0.6327,秩和检验:8.0065e-09
GWO：最差值: 1.3589e-13,最优值:6.4837e-14,平均值:1.0036e-13,标准差:1.9356e-14,秩和检验:7.3694e-09
WOA：最差值: 7.9936e-15,最优值:8.8818e-16,平均值:3.908e-15,标准差:2.6473e-15,秩和检验:2.1716e-05
IWOA：最差值: 8.8818e-16,最优值:8.8818e-16,平均值:8.8818e-16,标准差:0,秩和检验:NaN
函数：F5
PSO：最差值: 2.527,最优值:1.2815,平均值:1.6516,标准差:0.32439,秩和检验:8.0065e-09
GWO：最差值: 0.029495,最优值:0,平均值:0.0064644,标准差:0.010063,秩和检验:0.0045321
WOA：最差值: 0.15438,最优值:0,平均值:0.0077188,标准差:0.034519,秩和检验:0.34211
IWOA：最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
函数：F6
PSO：最差值: 78.0917,最优值:36.101,平均值:57.2082,标准差:13.0797,秩和检验:8.0065e-09
GWO：最差值: 9.4769,最优值:5.6843e-14,平均值:2.4972,标准差:3.4197,秩和检验:7.4242e-09
WOA：最差值: 5.6843e-14,最优值:0,平均值:2.8422e-15,标准差:1.2711e-14,秩和检验:0.34211
IWOA：最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN