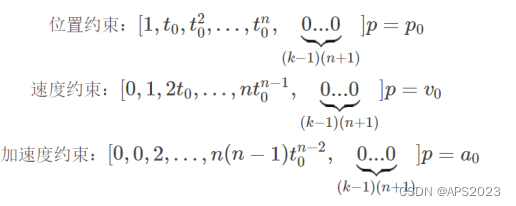自动驾驶算法（十）：多项式轨迹与Minimun Snap闭式求解原理及代码讲解

本文主要是介绍自动驾驶算法（十）：多项式轨迹与Minimun Snap闭式求解原理及代码讲解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1 多项式轨迹与Minimun Snap闭式求解原理

2 代码解析

1 多项式轨迹与Minimun Snap闭式求解原理

        我们上次说的Minimun Snap，其实我们就在求一个二次函数的最优解：

        也就是优化函数 $p^TQp$ 在约束 $Ap=b$ 下的最小值。

        但这是一个渐进最优解而不是解析最优解，是否有一个解析最优解呢？

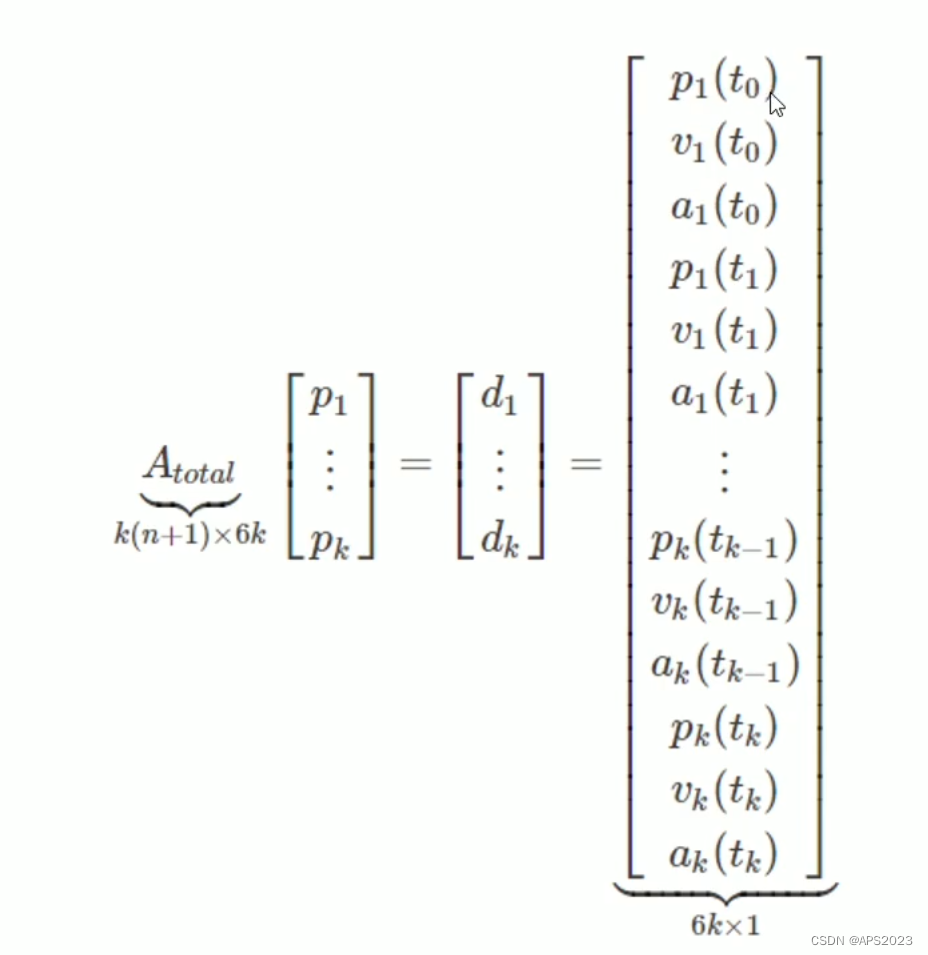
        我们用 $Ap = d$ 的形式表达：（d表示每一段路程中的起点和终点的位置、速度、加速度），比如 $p_{1}(t_0),v_{1}(t_0),a_{1}(t_0),p_{1}(t_1),v_{1}(t_1),a_{1}(t_1)$ 表示第一段起点的位置、速度、加速度、第一段终点的位置、速度、加速度。段数是k段，每段有起点和终点、起点终点有位置、速度加速度三个变量、因此维度为2*3k = 6k。

        因此我们可以求出一个确定的p，带入 $p^TQp$ 后就计算出来了我们的最小值。

        A矩阵的维度就是一共有K段每段是n+1阶的参数，各个段的位置为6，因此维度为k(n+1) * 6K

                                                 $A_{total} \begin{bmatrix} p_1\\p_2 \\... \\... \\p_k \end{bmatrix} = \begin{bmatrix} d_1\\d_2 \\... \\... \\d_k \end{bmatrix}$

        更进一步的说：

         $p = A^{-1}d$ 就是我们要求解的方程。

        我们不妨先看一段，即第一段和第二段： $p_i$ 表示第i段。我画了个图：

        那么 $t^{(i)}$ 这个时间点就是1段的末尾和2段的初始点。

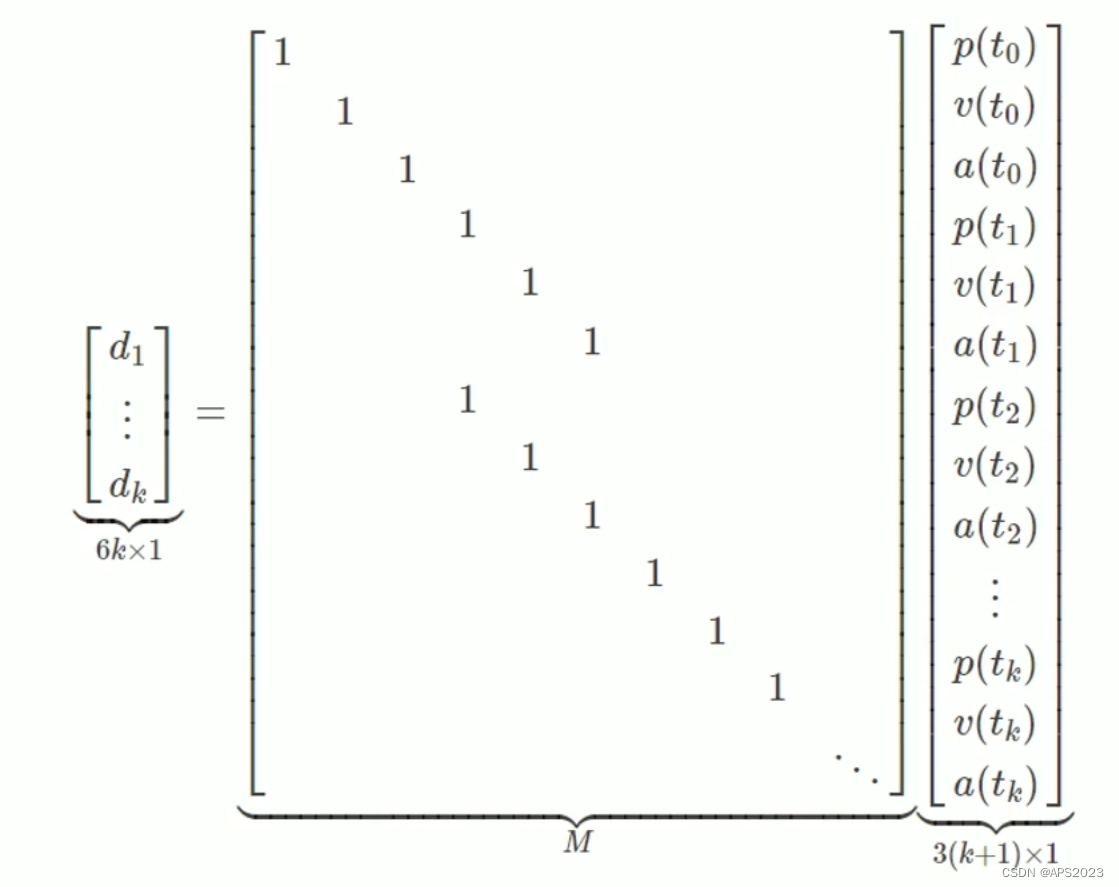
        我们消除重复变量：

        我们一共是k+1个航路点，每个航路点有p、v、a。因此矩阵大小为3(k+1)。

        我们得到 d = Md'

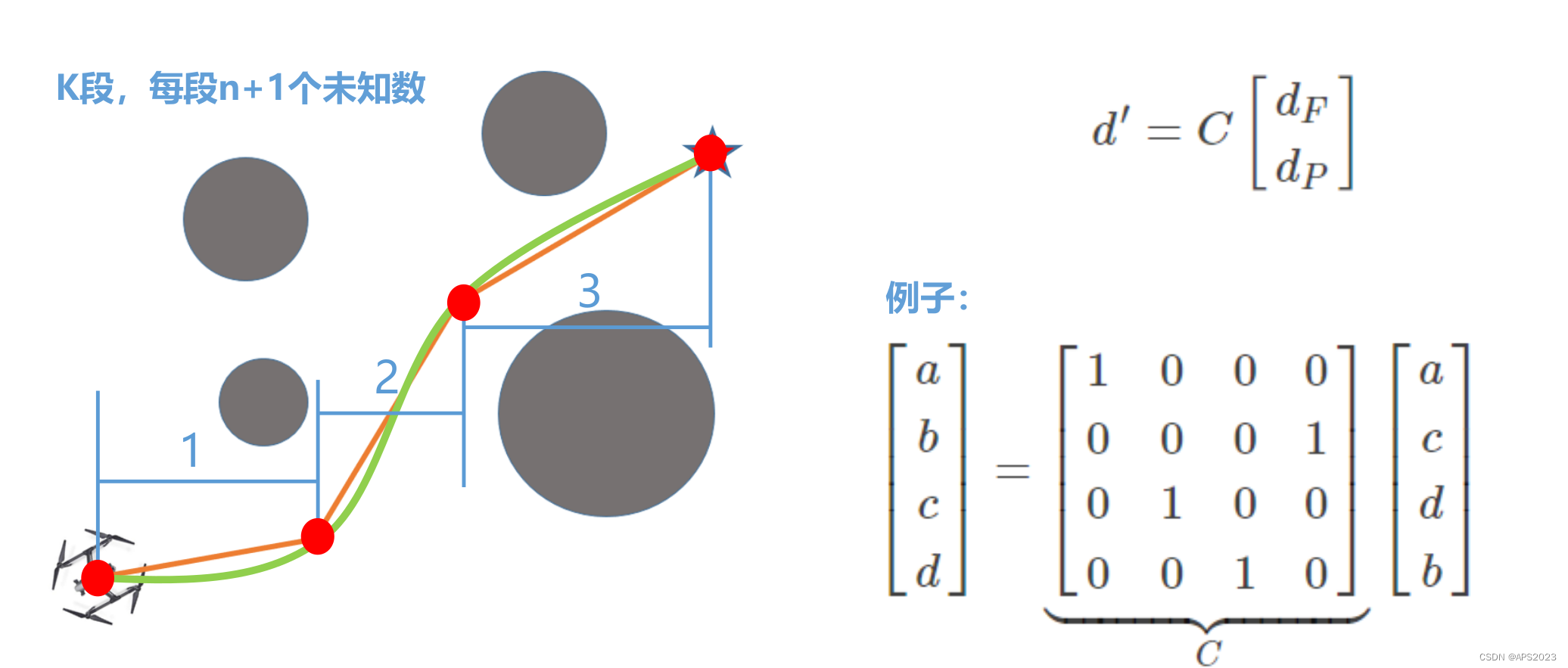
        d' = C[dF dP]T，这里dF表示已知量，包括起点、终点的位移、速度、加速度，也包括中点间的已知量（我们要经过这些点）。dP表示未知量。我们可以看一个简单的例子：

        我们把它写到一起：

        我们就是dP未知，因此我们对dP求导，因此可以求出来dP的解析解。

        我们可以手动增加航路点避免碰撞：

        我们来总结一下闭式求解的步骤：

2 代码解析

        我们只讲解和上篇博客不一样的地方：

        我们先看一下运行结果：

        我们来进行代码复现：
function polys = minimum_snap_single_axis_close_form(wayp,ts,n_order,v0,a0,v1,a1)
% 参数个数 = 阶数+1
n_coef = n_order+1;
% 多项式的段数:航路点-1
n_poly = length(wayp)-1;
% 计算Q 和原来的一样
Q_all = [];
for i=1:n_polyQ_all = blkdiag(Q_all,computeQ(n_order,3,ts(i),ts(i+1)));
end
这里依旧用n_coef表示参数个数（数量为拟合曲线的最大阶数+1），用n_poly表示多项式的段数，大小为航路点数量-1，Q的构造方式和上篇博客一致，不再赘述。

我们来看闭式求解的步骤，我们先来计算A矩阵：
% compute A (n_continuous*2*n_poly) * (n_coef*n_poly)
n_continuous = 3;  % 1:p  2:pv  3:pva  4:pvaj  5:pvajs
% A的维度是 3*2*K（航路点个数） 阶数（N+1） * K
A = zeros(n_continuous*2*n_poly,n_coef*n_poly);
% 遍历每一段航路点
for i = 1:n_poly% 位置、速度、加速度for j = 1:n_continuous% 计算具体参数 j--参数个数（阶数+1）for k = j:n_coefif k==jt1 = 1;t2 = 1;else %k>jt1 = tk(i,k-j+1);t2 = tk(i+1,k-j+1);end% 每一段填充首和尾A(n_continuous*2*(i-1)+j,n_coef*(i-1)+k) = prod(k-j+1:k-1)*t1;A(n_continuous*2*(i-1)+n_continuous+j,n_coef*(i-1)+k) = prod(k-j+1:k-1)*t2;endend
end
        我们知道，如果我们的航路点是K段，我们要拟合多项式的次数为N。因此我们的A矩阵大小为航路点为K段，每段的话有起终点、每个起终点有X、V、A三个元素，因此我们的矩阵大小为 K*2*3 * （N+1）*K。

        先给它初始化为0。我们遍历每一段航路点，先计算这段航路点的位移、速度、加速度。

        然后我们计算M矩阵：
M = zeros(n_poly*2*n_continuous,n_continuous*(n_poly+1));
for i = 1:n_poly*2j = floor(i/2)+1;rbeg = n_continuous*(i-1)+1;cbeg = n_continuous*(j-1)+1;M(rbeg:rbeg+n_continuous-1,cbeg:cbeg+n_continuous-1) = eye(n_continuous);
end
M
计算C矩阵和K矩阵：
% compute C
num_d = n_continuous*(n_poly+1);
C = eye(num_d);
df = [wayp,v0,a0,v1,a1]';% fix all pos(n_poly+1) + start va(2) + end va(2) 
fix_idx = [1:3:num_d,2,3,num_d-1,num_d];
free_idx = setdiff(1:num_d,fix_idx);
C = [C(:,fix_idx) C(:,free_idx)];% K
AiMC = inv(A)*M*C;
R = AiMC'*Q_all*AiMC;n_fix = length(fix_idx);
Rff = R(1:n_fix,1:n_fix);
Rpp = R(n_fix+1:end,n_fix+1:end);
Rfp = R(1:n_fix,n_fix+1:end);
Rpf = R(n_fix+1:end,1:n_fix);
计算p恢复轨迹、位置、加速度：
dp = -inv(Rpp)*Rfp'*df;p = AiMC*[df;dp];polys = reshape(p,n_coef,n_poly);