哈希表及处理冲突的常用方法

内容会持续更新，有错误的地方欢迎指正，谢谢!

前言

哈希法又称散列法，相应的表称为哈希表或散列表。
基本思想：

1. 先在元素的关键字k和元素的存储位置p之间建立一个对应关系H，使得p=H(k)，H称为哈希函数。创建哈希表时，把关键字为k的元素直接存入地址为H(k)的单元；
2. 以后当查找关键字为k的元素时，再利用哈希函数计算出该元素的存储位置p=H(k)，从而达到按关键字直接存取元素的目的。

值不同的多个关键字可能会映射到哈希表的同一地址上，即 k1≠k2 ，但 H（k1）=H（k2），这种现象称为冲突。实际中，冲突是不可避免的，只能通过改进哈希函数的性能来减少冲突。

常用的构造哈希函数的方法

构造哈希函数的原则是： 1. 函数本身便于计算；2. 计算出来的地址分布均匀，即对任一关键字k，f(k) 对应不同地址的概率相等。

1.除留余数法：
假设哈希表长为m，p为小于等于m的最大素数，则哈希函数为h（k）=k % p 。
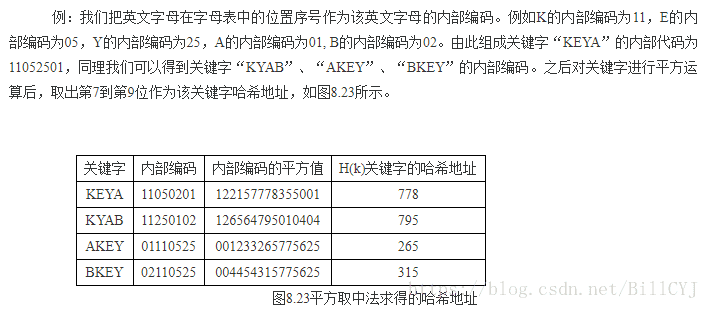
2.平方取中法：
先求出关键字的平方值，然后按需取平方值的中间几位作为哈希地址。这是因为：平方后中间几位和关键字中每一位都相关，故不同关键字会以较高的概率产生不同的哈希地址。

常用的处理冲突的方法

创建哈希表和查找哈希表都会遇到冲突，两种情况下解决冲突的方法应该一致。
下面以创建哈希表为例，说明解决冲突的方法。
常用的解决冲突方法有以下四种：

1.开放地址法：

基本思想是：当关键字key的哈希地址p=H（key）出现冲突时，以p为基础，产生另一个哈希地址p1，如果p1仍然冲突，再以p为基础，产生另一个哈希地址p2，…，直到找出一个不冲突的哈希地址pi ，将相应元素存入其中。
这种方法有一个通用的再散列函数形式：Hi=（H（key）+di）% m i=1，2，…，n

其中di称为增量序列。增量序列的取值方式不同，相应的再散列方式也不同。主要有以下三种：

1. 线性探测再散列 di=1，2，3，…，m-1
   这种方法的特点是：冲突发生时，顺序查看表中下一单元，直到找出一个空单元或查遍全表。
2. 二次探测再散列 di=12，-12，22，-22，…，k2，-k2 ( k<=m/2 )
   这种方法的特点是：冲突发生时，在表的左右进行跳跃式探测，比较灵活。
3. 伪随机探测再散列 di=伪随机数序列
   具体实现时，应建立一个伪随机数发生器，（如i=(i+p) % m），并给定一个随机数做起点。

2.链地址法：

基本思想是将所有哈希地址为 i 的元素构成一个称为同义词链的单链表，并将单链表的头指针存在哈希表的第i个单元中，因而查找、插入和删除主要在同义词链中进行。链地址法适用于经常进行插入和删除的情况。

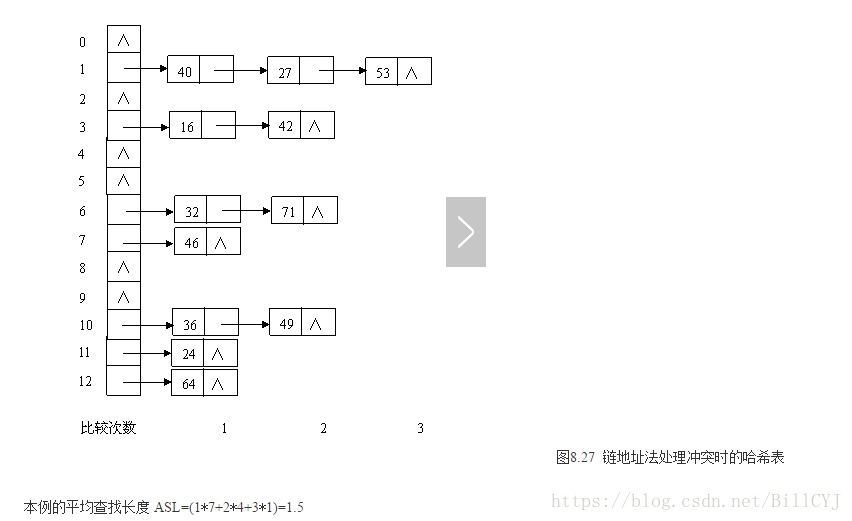
例如，已知一组关键字（32，40，36，53，16，46，71，27，42，24，49，64），哈希表长度为13，哈希函数为：H（key）= key % 13，则用链地址法处理冲突的结果如图8.27所示：

本例的平均查找长度 =(1*7+2*4+3*1)/12=1.5

3.再哈希法：

这种方法是同时构造多个不同的哈希函数：Hi=RH1（key） i=1，2，…，k
当哈希地址Hi=RH1（key）发生冲突时，再计算Hi=RH2（key）……，直到冲突不再产生。这种方法不易产生聚集，但增加了计算时间。

解决冲突的方法的总结：

1. 开放地址法：计算简单快捷，处理起来方便，但线性探测法容易形成“堆聚”。另外，该方法的删除操作显得十分复杂，我们不能直接删除关键字所在的记录，否则在查找删除位置后面的元素时，可能会出现找不到的情况，因为删除位置上已经成了空地址，查找到这里时会终止查找。所以，就需要重建哈希表，特别浪费性能。
2. 链地址法：该方法将所有哈希地址相同的结点构成一个单链表，单链表的头结点存在哈希数组里，链地址法常出现在经常插入和删除的情况下，此时，哈希表的插入/删除/查找都是O(1)的时间复杂度。该法不会出现“堆聚”现象，哈希地址不同的关键字不会发生冲突；不需要重建哈希表。另外，如果开放地址法中，哈希表里存满关键字了就需要扩充哈希表然后重建哈希表，而链地址法不需要。