力扣日记1.13-【二叉树篇】669. 修剪二叉搜索树

本文主要是介绍力扣日记1.13-【二叉树篇】669. 修剪二叉搜索树，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

力扣日记：【二叉树篇】669. 修剪二叉搜索树

日期：2023.1.13
参考：代码随想录、力扣

669. 修剪二叉搜索树

题目描述

难度：中等

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树不应该改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。可以证明，存在唯一的答案。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：
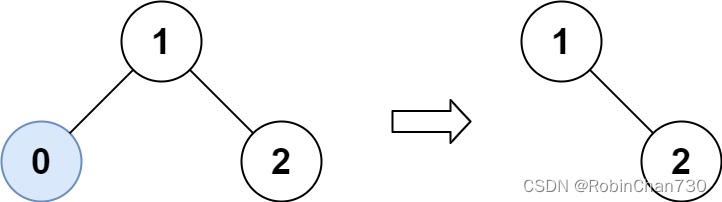
在这里插入图片描述

输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

示例 2：
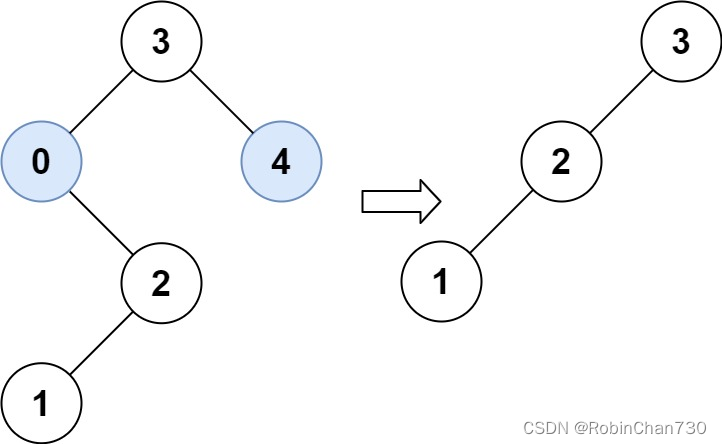
在这里插入图片描述

输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

提示：

树中节点数在范围 [1, 10^4] 内
0 <= Node.val <= 10^4
树中每个节点的值都是唯一的
题目数据保证输入是一棵有效的二叉搜索树
0 <= low <= high <= 10^4

题解

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:// 递归的返回值：当前root树经过修剪后的新根节点TreeNode* trimBST(TreeNode* root, int low, int high) {// 终止条件：遇到空节点就返回空if (root == nullptr)    return root;// 如果root的值小于low，此时root以及root的左子树一定是要删除的// 但是root的右子树(大于root)可能存在满足条件的，所以要对root的右子树进行修剪，并将修剪后的右子树根节点返回给root的上一层来接收(因为这里的root是要被删除的，所以是返回给root的上一层)if (root->val < low) {return trimBST(root->right, low, high); // 对root的右子树进行修剪，并将新的右子树根节点返回给上一层} // 大于high的情况也是同理，此时对root的左子树进行修剪，并返回新的左子树根节点给上一层else if (root->val > high) {return trimBST(root->left, low, high);}// 如果当前root满足条件，但其左右子树可能存在不满足条件的// 则对其左右子树分别进行修剪root->left = trimBST(root->left, low, high);    // 左子树修剪后作为root的左节点(这里当前层可能就会接收来自root的左节点的下一层的根节点)root->right = trimBST(root->right, low, high);  // 右子树同理// 返回当前rootreturn root;}
};

复杂度

时间复杂度：
空间复杂度：

思路总结

本题相比于前两道的插入和删除，还是复杂了许多，且不同于以往的递归，本题在不符合处理（如这里的删除）条件时需要递归，在符合处理（删除）条件时也要递归！！！（以前一般都是只需要在不符合类似于中节点的处理条件的时候进行递归）
这里要明确理解递归函数的意义：即对传入的root树进行修剪，并返回修剪后的树的新根节点
且读题要准确，是节点值不在[low, high]范围的要剔除
因此，删除时要分别对小于low和大于high的情况进行处理：
- 对于root的值小于low的情况，：
  - 此时root以及root的左子树一定是要删除的
  - 但是root的右子树(大于root)可能存在在范围内的节点，所以要对root的右子树进行修剪，并将修剪后的右子树根节点返回给root的上一层来接收(因为这里的root是要被删除的，所以是返回给root的上一层)
  - 这里要理解“返回给上一层”的含义：即return后，是由root的上一层去接收的
    
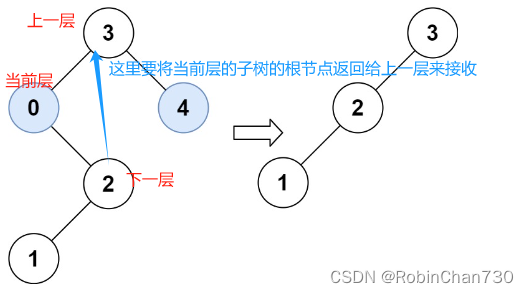
    对应于代码中就是
    当前层（这里的0）：
```
if (root->val < low) {return trimBST(root->right, low, high); // 对root的右子树进行修剪，并将新的右子树根节点返回给上一层
} 
```
    而return后回到上一层（即3），会接收来自0的右子树的根节点
```
root->left = trimBST(root->left, low, high);    // 左子树修剪后作为root的左节点(这里当前层可能就会接收来自root的左节点的下一层的根节点)
```
- 对于root的值大于high的情况处理是同理的。
在写代码时，就按注释时的思路：
- 终止条件：遇到空节点就返回空
- 如果root的值小于low
  - 此时对root的右子树进行修剪，并将修剪后的右子树根节点返回给root的上一层来接收
- 如果root的值大于high
  - 此时对root的左子树进行修剪，并返回新的左子树根节点给上一层
- 如果root的是符合条件的（但其左右子树可能存在不满足条件需要修剪的）
  - 则对其左右子树分别进行修剪，此时要用root的左右节点去接收，即：
  - 左子树修剪后作为root的左节点
  - 右子树同理
- 最后返回root