《剑指 Offer》专项突破版 - 面试题 8 : 和大于或等于 k 的最短子数组（C++ 实现）- 详解同向双指针（滑动窗口算法）

本文主要是介绍《剑指 Offer》专项突破版 - 面试题 8 : 和大于或等于 k 的最短子数组（C++ 实现）- 详解同向双指针（滑动窗口算法），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

一、暴力求解

二、同向双指针（滑动窗口算法）

前言

题目链接：. - 力扣（LeetCode）

题目：

输入一个正整数组成的数组和一个正整数 k，请问数组中和大于或等于 k 的连续子数组的最短长度是多少？如果不存在所有数字之和大于或等于 k 的子数组，则返回 0。例如，输入数组 [5, 1, 4, 3]，k 的值为 7，和大于或等于 7 的最短连续子数组是 [4, 3]，因此输出它的长度 2。

分析：

子数组由数组中一个或连续的多个数字组成。一个子数组可以用两个指针表示。如果第 1 个指针 left 指向子数组的第 1 个数字，第 2 个指针 right 指向子数组的最后一个数字，那么子数组就是由这两个指针之间的所有数字组成的。

一、暴力求解

先固定指针 left（最开始指向数组中的第 1 个元素）。
然后从 left 开始不断向右移动指针 right，直到两个指针之间的子数组中所有数字之和大于或等于 k（子数组的长度为 right - left + 1），或者 right 超出范围，即不存在和大于或等于 k 的子数组。
如果不存在和大于或等于 k 的子数组，则说明已经尝试了所有的可能性，可以结束这个查找的过程了；否则 ++ left，然后重复步骤 1 和 2，直到 left 超出范围。

这种解法的时间复杂度是 O(n^2)。

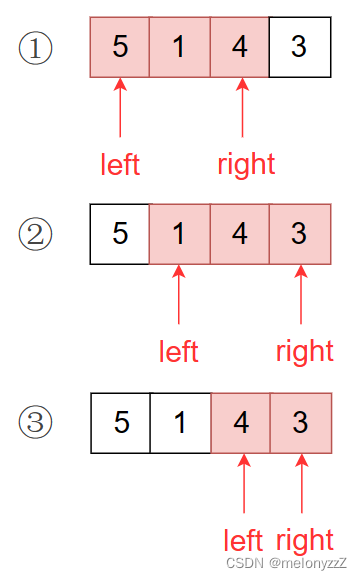
当 left = 0 时，right 的最优解为 2（right >= 2 && right < 4，两个指针之间的子数组中所有数字之和大于或等于 k）；

当 left = 1 时，right 的最优解为 3；

当 left = 2 时，right 的最优解为 3；

当 left = 3 时，right 没有解。

class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int n = nums.size();int minLen = n + 1;for (int left = 0; left < n; ++left){int sum = 0;for (int right = left; right < n; ++right){sum += nums[right];if (sum >= target){if (right - left + 1 < minLen)minLen = right - left + 1;break;}}if (sum < target)break;}return minLen == n + 1 ? 0 : minLen;}
};

二、同向双指针（滑动窗口算法）

可以对上述解法进行优化。指针 left 和 right 初始化的时候指向数组的第 1 个元素。

不断向右移动指针 right，直到两个指针之间的子数组数字之和大于或等于 k（子数组的长度为 right - left + 1）。
停止右移指针 right，转而不断向右移动指针 left，直到两个指针之间的子数组数字之和小于 k。注意：指针 left 每向右移动一步，如果两个指针之间的子数组数字之和大于或等于 k，那么就要更新最短子数组的长度，这相当于利用了第 1 步产生的结果。
重复步骤 1 和 2，直到 right 超出范围。

class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int n = nums.size();int minLen = n + 1;int left = 0;int sum = 0;for (int right = 0; right < n; ++right){sum += nums[right];while (sum >= target){if (right - left + 1 < minLen)minLen = right - left + 1;sum -= nums[left];++left;}}return minLen == n + 1 ? 0 : minLen;}
};