半数集问题(算法设计与分析)

本文主要是介绍半数集问题(算法设计与分析)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

给定一个自然数n给定一个自然数n，由n 开始可以依次产生半数集set(n)中的数如下。
(1) n∈set(n)；
(2) 在n 的左边加上一个自然数，但该自然数不能超过最近添加的数的一半；
(3) 按此规则进行处理，直到不能再添加自然数为止。
例如，set(6)={6,16,26,126,36,136}。半数集set(6)中有6 个元素。
注意半数集是多重集。
对于给定的自然数n，计算半数集set(n)中的元素个数。
输入样例：

6

输出样例：

6

算法设计
首先，先了解一下半数集是如何产生的，以set(6)为例,有如下图示:
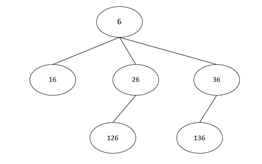
在这里插入图片描述

我们找到了三个满足条件的数，即1、2、3,他们分别与6构成了16、26、36,依照这三个数继续向集合中添加元素，对于16，1是最近添加的数,但因为比1的一半小的自然数只有0，所以这一步就结束了。对于26，2是最近添加的数，1满足(2)的条件，所以将126也添加到了半数集中。同理，将136也添加到了半数集中。
由此，我们可以应用递归的思想，来解决问题，对于set(n)中的元素个数f(n)，有以下公式：
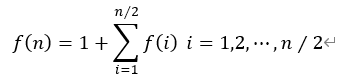
在这里插入图片描述

设计的递归算法如下：

int halfset(int n){int sum = 1;for(int i=1;i<=n/2;i++){sum += halfset(i);}return sum;
}

该算法在n较大时，运行时间较长，原因是进行了很多重复的递归。比如n=16时,满足条件的数中有4和8,在对8进行递归中，也包含了4这个数，这样就产生了重复。我们可以设置一个数组，存放已经计算好的结果，改进算法的效率，改进的代码如下所示:

int a[1005]={0};
int dfs(int n){int sum = 1;if(a[n]>0)return a[n];for(int i=1;i<=n/2;i++){sum += dfs(i);}a[n]=sum;return sum;
}

完整代码:

#include<bits/stdc++.h>
using namespace std;
int a[1005]={0}; //存放已计算的数据
int halfset(int n){int sum = 1;if(a[n]>0) //如果f(n)已经得出，就不必再重复计算return a[n];for(int i=1;i<=n/2;i++){sum += halfset(i);}a[n]=sum;return sum;
}
int main()
{int n;FILE* fin=fopen("input.txt","r+");FILE* fout=fopen("output.txt","r+");fscanf(fin,"%d",&n);int result=halfset(n);cout << result <<endl;fprintf(fout,"%d",result);fclose(fin);fclose(fout);return 0;
}