【算法】最佳牛围栏（二分，前缀和，双指针）

本文主要是介绍【算法】最佳牛围栏（二分，前缀和，双指针），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目

农夫约翰的农场由 N 块田地组成，每块地里都有一定数量的牛，其数量不会少于 1 头，也不会超过 2000 头。

约翰希望用围栏将一部分连续的田地围起来，并使得围起来的区域内每块地包含的牛的数量的平均值达到最大。

围起区域内至少需要包含 F 块地，其中 F 会在输入中给出。

在给定条件下，计算围起区域内每块地包含的牛的数量的平均值可能的最大值是多少。

输入格式

第一行输入整数 N 和 F，数据间用空格隔开。

接下来 N 行，每行输入一个整数，第 i+1 行输入的整数代表第 i 片区域内包含的牛的数目。

输出格式

输出一个整数，表示平均值的最大值乘以 1000 再 向下取整 之后得到的结果。

数据范围

1 ≤ N ≤ 100000
1 ≤ F ≤ N

输入样例：

输出样例：

思路

将每个农场的牛的数量存储到数组a[ ]中，二分平均值（答案），check（）函数用来判断二分出来的平均值是否符合要求。

其中s[ ]数组是由s[i] = s[i - 1] + a[i] - avg; 得出来的 s[i]表示a[1]~a[ i ]中农场中牛的个数的平均值，由此可知，s[j] - s[i] 代表（i，j]的牛的数量的平均值。如下图所示：

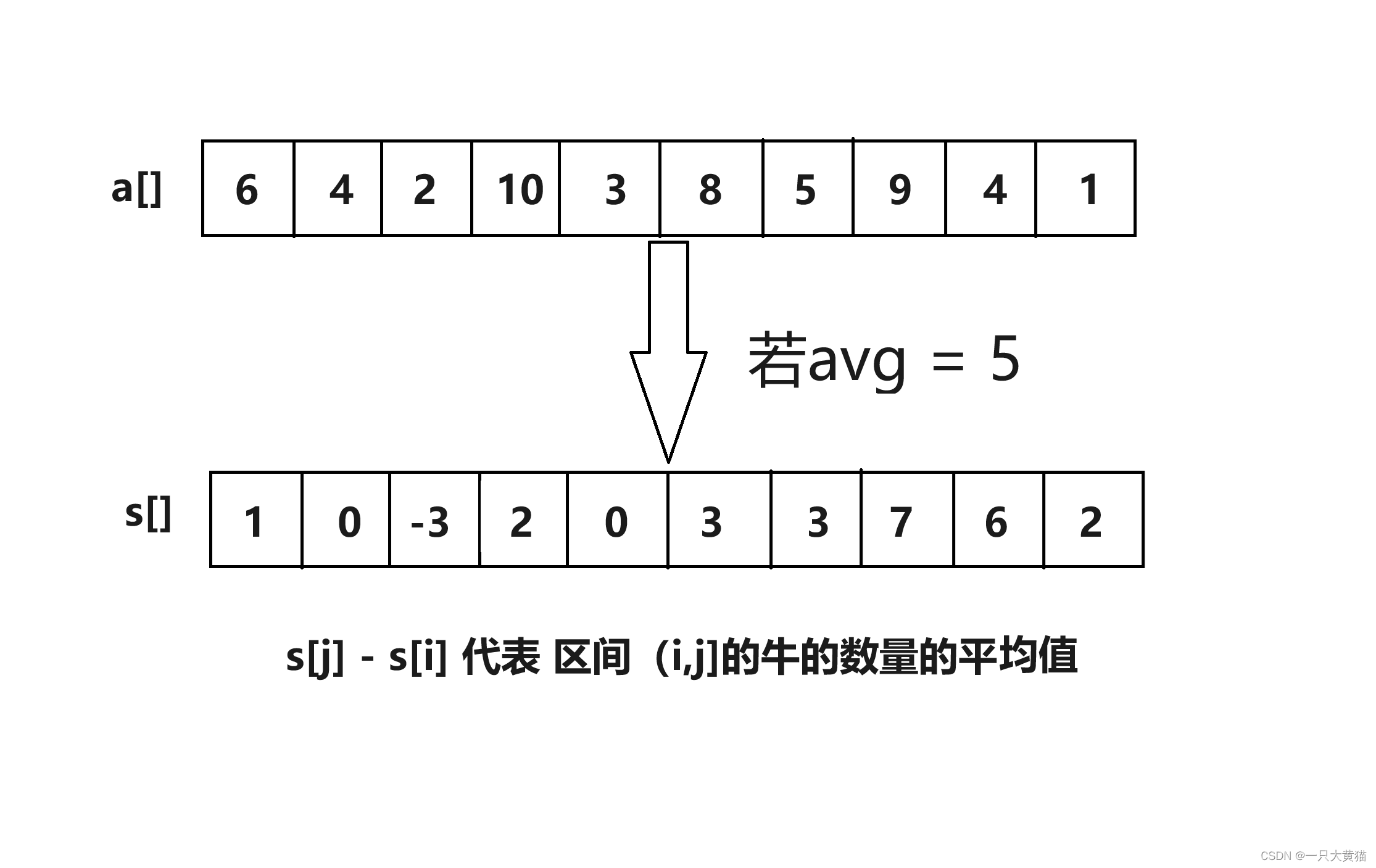
check()数组代码：

代码

#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
int n,f;
double a[N],s[N];bool check(double avg)
{for(int i = 1; i <= n; i ++) s[i] = s[i - 1] + a[i] - avg;// 求出来前缀和double mins = 0;for(int k = f; k <= n; k ++){mins = min(mins,s[k - f]);// 求出区间为f的农场牛的平均值的最小值if(s[k] - mins >= 0) return true;// 判断}return false;
}int main()
{cin >> n >> f;double l = 0,r = 0;for(int i = 1; i <= n; i ++){cin >> a[i];r = max(r,a[i]);}while(r - l > 1e-5){double mid = (l + r) / 2;if(check(mid)) l = mid;else r = mid;}printf("%d",(int)(r * 1000));return 0;
}

题目来自： 102. 最佳牛围栏 - AcWing题库

难度：简单

时/空限制：1s / 64MB

总通过数：16264

总尝试数：39506

来源：《算法竞赛进阶指南》, POJ2018, kuangbin专题

算法标签：二分