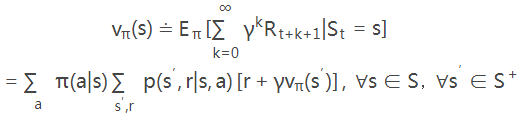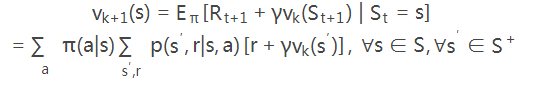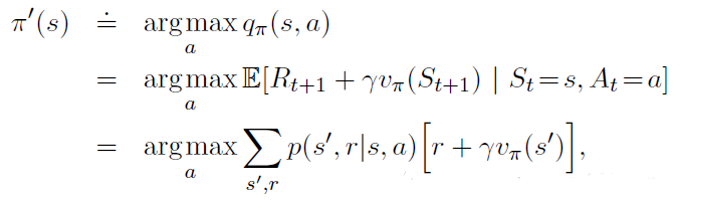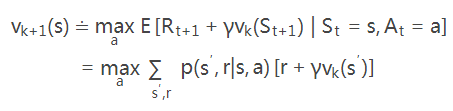本文主要是介绍人工智障学习笔记——强化学习(2)基于模型的DP方法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
上一章我们引入了马尔科夫决策过程的概念:
马尔可夫决策过程是一个五元组(S,A,P(),R(),γ) 其中:
1)S是一组有限的状态,即状态集 (states)
2)A是一组有限的行为(或者,As 是从状态可用的有限的一组行动s),即动作集 (Action)
3)Pa(s,s')=Pr(st+1=s'midst=s,at=a)表示状态 s 下采取动作 a 之后转移到 s' 状态的概率
4)Ra(s,s')是状态 s 下采取动作 a 获得的奖励(或期望的直接奖励)
5)γ→[0,1]是折现系数,代表未来奖励与现在奖励之间的重要差异,也叫做衰减因子
同时我们知道强化学习的目标是找到最优策略π使得累计回报的期望最大。我们也可以这样理解,强化学习可以看作为序列决策问题。即找到一个决策序列使得目标函数最优。所谓的累积回报其背后的含义是评价策略完成任务的回报,所以目标函数等价于任务。强化学习的直观目标是找到最优策略,其目的是更好地完成任务。回报函数对应着具体的任务,所以强化学习所学到的最优策略是跟具体的任务相对应的。从这个意义上来说,强化学习并不是万能的,它无法利用一个算法实现所有的任务。
强化学习可以分为两大类,根据马尔可夫决策过程五元组(S,A,P(),R(),γ)里的转移概率P是否已知,可以分为基于模型的强化方法和基于无模型的强化学习方法。
基于模型的强化学习可以利用动态规划(dynamic programming)的思想来解决。想了解动态规划的同学可以参考ACM分类里的一些关于动态规划的文章http://blog.csdn.net/sm9sun/article/details/53240542
(不过都是少年时期的代码了,有点LOW)
我们已知满足动态规划的几个基本性质:
一、最优子结构
二、子问题重叠
三、同级问题独立
简单来说就是整个优化问题可以分解为多个子优化问题,子优化问题的解可以被存储和重复利用。
马尔科夫决策过程利用贝尔曼最优性原理得到贝尔曼最优化方程:
从方程中可以看到,马尔科夫决策问题符合使用动态规划的两个条件,因此可以利用动态规划解决马尔科夫决策过程的问题。动态规划的核心是找到最优值函数。经典DP算法在强化学习中的实用性有限,因为他们假定了一个具体的模型,并且还受限于它们的计算cost很高,但它在理论上仍然很重要。
通用策略迭代是:
1. 先从一个策略π0开始,
2. 策略评估(Policy Evaluation) - 得到策略π0的价值vπ0
3. 策略改善(Policy Improvement) - 根据价值vπ0,优化策略π0。
4. 迭代上面的步骤2和3,直到找到最优价值v*,因此可以得到最优策略π*(终止条件:得到了稳定的策略π和策略价值vπ)。
这个被称为通用策略迭代(Generalized Policy Iteration)。
策略评估是通过状态值函数来实现的,值函数定义为(S+比S多了一个终止状态):
此时,s状态的值函数是由其他所有状态在策略π下的值函数确定,这是无法计算的。所以DP通过当前的策略π计算下一时刻的状态值函数。在多次迭代后(k→∞),vk≈vπ
而策略改善通过最大化动作状态值函数实现的:
价值迭代方法是对上面所描述的方法的一种简化:
在策略评估过程中,对于每个状态s,只找最优(价值是最大的)行动a。这样可以减少空间的使用。步骤如下:
1. 初始化 - 所有状态的价值(比如:都设为0)。
2. 初始化 - 一个等概率随机策略π0(the equiprobable random policy)
3. 策略评估
对于每个状态s,只找最优(价值是最大的)行动a。即:
一般来说值迭代和策略迭代都需要经过无数轮迭代才能精确的收敛到V*和π*, 而实践中,我们往往设定一个阈值来作为中止条件,即当Vπ(s)值改变很小时,我们就近似的认为获得了最优策略。在折扣回报的有限MDP(discounted finite MDPs)中,进过有限次迭代,两种算法都能收敛到最优策略π*。
至此我们了解了马尔可夫决策过程的动态规划解法,动态规划的优点在于它有很好的数学上的解释,但是动态要求一个完全已知的环境模型,这在现实中是很难做到的。另外,当状态数量较大的时候,动态规划法的效率也将是一个问题。
vπ
这篇关于人工智障学习笔记——强化学习(2)基于模型的DP方法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!