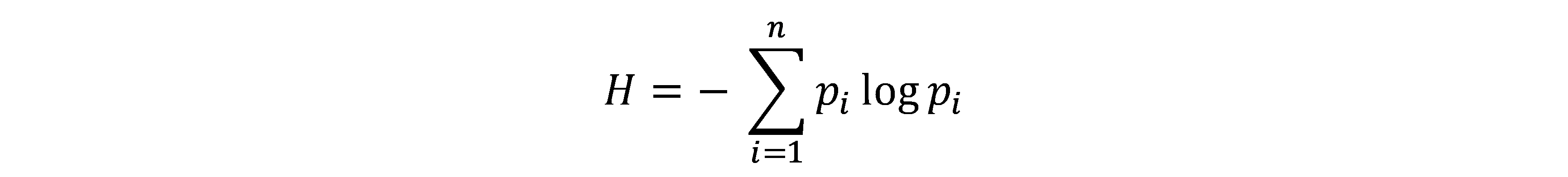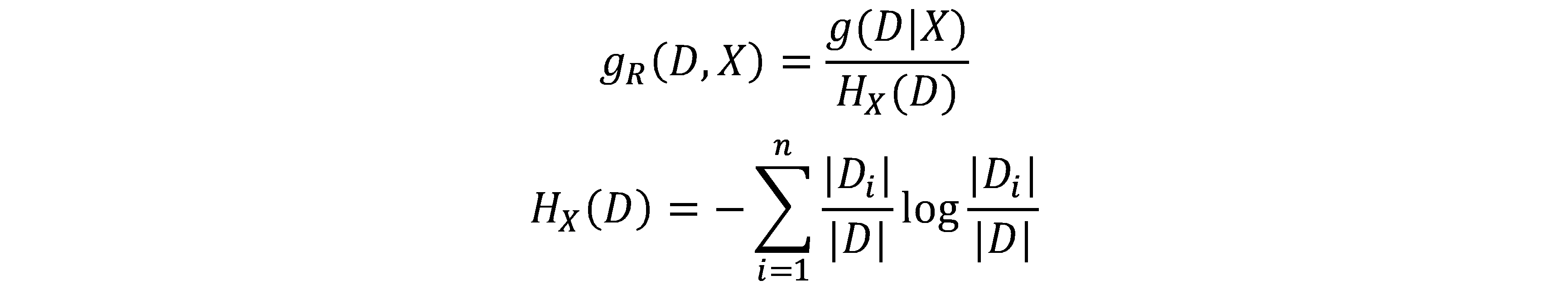本文主要是介绍分类——决策树ID3与C4.5以及Python实现,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
决策树算法是一个分类算法,ID3以及C4.5决策树是多叉树。
核心思想:根据特征及对应特征值组成元组为切分点切分样本空间。
基本概念:
熵(entropy):该词最初来自于热力学,用来表示系统的混乱程度。香农借用该词表示一个随机过程的不确定性程度,即香农熵。式中Pi指随机变量取某个值的概率。
条件熵(conditional entropy):给定一个划分数据的条件X=x,那么随机变量Y的随机程度将下降。正如一个热力学系统,在外力做功的情况下,系统熵下降。下降后的熵就是基于条件X=x的条件熵。
实际计算,就是根据特征Y的取值将数据集划分成若干子数据集,分别计算子数据集的熵,然后以子数据集占比为权重求平均值。
信息增益(information gain):加入限制条件后,信息的随机性减少程度。即划分前的熵与条件熵的差。特征X对数据集D的信息增益为:
由公式可知,计算条件熵时,特征X若取值较多,那么数据划分更细,则条件熵偏向于减小,极端情况下,每个样本都是独一无二的,那么条件熵为0。信息增益就偏向于取值多的特征,进行更多的划分,故引入信息增益比。
信息增益比(informationgain ratio):
其中,n就是特征X不同取值的个数,也即子数据集的个数。分母是数据集自身划分引起的熵变。显然,划分越多,熵越大。
优点:
1. 容易解释,可视化。模型是“白箱”
2. 无需过多数据准备
3. 预测过程时间复杂度为log(n)
4. 能够处理连续以及离散值
5. 能够很好处理多分类问题
缺点:
1. 容易过拟合。可通过剪枝等方法减轻
2. 稳定性差。可通过集成学习改进
3. 学习过程是一个NP完全问题
4. 模型不能表示XOR等概念
5. 对类不平衡样本集敏感
算法流程:
Input: 阈值epsilon, 训练数据集X, y
Output: 决策树
- Step1:初始化,构建特征集及空树。
- Step2:递归构建决策树。
参数:特征集,子训练数据集X_data, y_data
递归终止条件:
1.集只有一个类,返回该类
2.特征集为空,返回最频繁的类
3.切分数据集前后,信息增益(比)小于epsilon
树的构建流程:
1. 计算每个特征的信息增益(比),以及切分的子数据集的索引。
2. 选取信息增益(比)最大的特征为最优特征,构建当前节点。
3. 从特征集中去除当前最优特征,并对相应的子数据集分别进行步骤1、2构建子树。
- Step3: 运用构建好的决策树进行预测。递归搜索树,碰到叶节点则返回类标记。
"""
ID3&C4.5决策树算法
"""
import math
from collections import Counter, defaultdictimport numpy as npclass node:# 这里构建树的节点类,也可用字典来表示树结构def __init__(self, fea=-1, res=None, child=None):self.fea = feaself.res = resself.child = child # 特征的每个值对应一颗子树,特征值为键,相应子树为值class DecisionTree:def __init__(self, epsilon=1e-3, metric='C4.5'):self.epsilon = epsilonself.tree = Noneself.metric = metricdef exp_ent(self, y_data):# 计算经验熵c = Counter(y_data) # 统计各个类标记的个数ent = 0N = len(y_data)for val in c.values():p = val / Nent += -p * math.log2(p)return entdef con_ent(self, fea, X_data, y_data):# 计算条件熵并返回,同时返回切分后的各个子数据集fea_val_unique = Counter(X_data[:, fea])subdata_inds = defaultdict(list) # 根据特征fea下的值切分数据集for ind, sample in enumerate(X_data):subdata_inds[sample[fea]].append(ind) # 挑选某个值对应的所有样本点的索引ent = 0N = len(y_data)for key, val in fea_val_unique.items():pi = val / Nent += pi * self.exp_ent(y_data[subdata_inds[key]])return ent, subdata_indsdef infoGain(self, fea, X_data, y_data):# 计算信息增益exp_ent = self.exp_ent(y_data)con_ent, subdata_inds = self.con_ent(fea, X_data, y_data)return exp_ent - con_ent, subdata_indsdef infoGainRatio(self, fea, X_data, y_data):# 计算信息增益比g, subdata_inds = self.infoGain(fea, X_data, y_data)N = len(y_data)split_info = 0for val in subdata_inds.values():p = len(val) / Nsplit_info -= p * math.log2(p)return g / split_info, subdata_indsdef bestfea(self, fea_list, X_data, y_data):# 获取最优切分特征、相应的信息增益(比)以及切分后的子数据集score_func = self.infoGainRatioif self.metric == 'ID3':score_func = self.infoGainbestfea = fea_list[0] # 初始化最优特征gmax, bestsubdata_inds = score_func(bestfea, X_data, y_data) # 初始化最大信息增益及切分后的子数据集for fea in fea_list[1:]:g, subdata_inds = score_func(fea, X_data, y_data)if g > gmax:bestfea = feabestsubdata_inds = subdata_indsgmax = greturn gmax, bestfea, bestsubdata_indsdef buildTree(self, fea_list, X_data, y_data):# 递归构建树label_unique = np.unique(y_data)if label_unique.shape[0] == 1: # 数据集只有一个类,直接返回该类return node(res=label_unique[0])if not fea_list:return node(res=Counter(y_data).most_common(1)[0][0])gmax, bestfea, bestsubdata_inds = self.bestfea(fea_list, X_data, y_data)if gmax < self.epsilon: # 信息增益比小于阈值,返回数据集中出现最多的类return node(res=Counter(y_data).most_common(1)[0][0])else:fea_list.remove(bestfea)child = {}for key, val in bestsubdata_inds.items():child[key] = self.buildTree(fea_list, X_data[val], y_data[val])return node(fea=bestfea, child=child)def fit(self, X_data, y_data):fea_list = list(range(X_data.shape[1]))self.tree = self.buildTree(fea_list, X_data, y_data)returndef predict(self, X):def helper(X, tree):if tree.res is not None: # 表明到达叶节点return tree.reselse:try:sub_tree = tree.child[X[tree.fea]]return helper(X, sub_tree) # 根据对应特征下的值返回相应的子树except:print('input data is out of scope')return helper(X, self.tree)if __name__ == '__main__':import timestart = time.clock()data = np.array([['青年', '青年', '青年', '青年', '青年', '中年', '中年','中年', '中年', '中年', '老年', '老年', '老年', '老年', '老年'],['否', '否', '是', '是', '否', '否', '否', '是', '否','否', '否', '否', '是', '是', '否'],['否', '否', '否', '是', '否', '否', '否', '是','是', '是', '是', '是', '否', '否', '否'],['一般', '好', '好', '一般', '一般', '一般', '好', '好','非常好', '非常好', '非常好', '好', '好', '非常好', '一般'],['否', '否', '是', '是', '否', '否', '否', '是', '是','是', '是', '是', '是', '是', '否']])data = data.TX_data = data[:, :-1]y_data = data[:, -1]from machine_learning_algorithm.cross_validation import validateg = validate(X_data, y_data, ratio=0.2)for item in g:X_data_train, y_data_train, X_data_test, y_data_test = itemclf = DecisionTree()clf.fit(X_data_train, y_data_train)score = 0for X, y in zip(X_data_test,y_data_test):if clf.predict(X) == y:score += 1print(score / len(y_data_test))print(time.clock() - start)我的GitHub
注:如有不当之处,请指正。
这篇关于分类——决策树ID3与C4.5以及Python实现的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!