本文主要是介绍MiniTab的正态性检验结果的分析，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
正态性检验概述
可使用 正态性检验 确定数据是否不服从正态分布。
执行菜单：要执行正态性检验，请选择统计 > 基本统计 > 正态性检验。
正态性检验 的假设
对于正态性检验，进行如下假设。
- H0：数据服从正态分布。
- H1：数据不服从正态分布。
正态性检验 的数据注意事项
- 数据必须为数字：您必须拥有数字数据，如包装重量。
- 样本数据应当是随机选择的：在统计学中，随机样本用于对总体做出归纳，即推断。如果数据不是随机收集的，则结果可能无法代表总体。
- 样本数量应当大于 20：如果样本数量小于 20，则提供的功效可能不足，无法检测样本数据和正态分布之间的显著差异。但是，在使用很大的样本数量时要格外小心，因为它们可能会提供过大的功效。当检验功效太大时，样本数据和理论分布之间可能无意义的小差异似乎会非常显著。
正态性检验 的示例
一家加工食品生产公司的科研人员想评估本公司生产的瓶装酱料的脂肪百分比。宣传的百分比为 15%。科研人员测量了 20 个随机样本的脂肪百分比。
样本 ID 脂肪百分比
1 15.2
2 12.4
3 15.4
4 16.5
5 15.9
6 17.1
7 16.9
8 14.3
9 19.1
10 18.2
11 18.5
12 16.3
13 20.0
14 19.2
15 12.3
16 12.8
17 17.9
18 16.3
19 18.7
20 16.2
科研人员想在执行假设检验之前验证正态性假设。
- 把上述数据输入到Minitab的数据表中。
- 选择统计 > 基本统计 > 正态性检验。
- 在变量中，输入脂肪百分比。
- 单击确定。
选择特定正态性检验
选择一个正态性检验。Anderson-Darling 适用于大多数情况。
- Anderson-Darling：对于检测数据分布尾部的非正态性而言，该检验通常比其他两种检验更有效。
- Ryan-Joiner：对于检测非正态性而言，该检验与 Anderson-Darling 具有类似的功能。
- Kolmogorov-Smirnov：该检验对于正态分布中的小偏差较不敏感。
指定 正态性检验 的百分位线
百分位线有两段与拟合分布线相交。共绘制两段，一段与数据刻度相交，另一段与百分比刻度相交。百分位线通常用于计算检验分数。例如，如果您想要知道第 95 个百分位的检验分数，则可以在 95% 处添加一条百分位线。Minitab 会计算相应的数据值。相反，如果您在数据值处添加一条百分位线，Minitab 会计算相应的百分比。
- 无：不显示百分位线。
- 在 Y 值：输入百分位线的 y 刻度值。输入介于 0 和 100 之间的值。
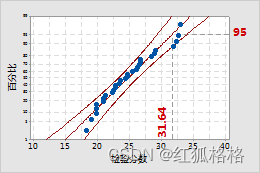eg：第 95 个百分位：排在第 95 个百分位的员工的检验分数为 31.64。换句话说，有 95% 的员工的分数为 31.64 或更少。
- 在数据值：输入百分位线的数据值。
eg：检验分数 27：检验分数 27 略高于第 70 个百分位，或者有略多于 70% 的员工的分数为 27 或更少。
解释结果
主要输出包括 p 值和概率图。
数据点离拟合的正态分布线相对较近。p 值大于显著性水平 0.05。因此，科学家无法否定数据服从正态分布这一原假设。
步骤 1：确定数据是否不服从正态分布
要确定数据是否不服从正态分布，请将 p 值与显著性水平进行比较。通常，显著性水平（用 α 或 alpha 表示）为 0.05 即可。显著性水平 0.05 表示当数据实际上服从正态分布时，断定数据不服从正态分布的风险为 5%。
P 值 ≤ α：数据不服从正态分布（否定 H0）
如果 p 值小于或等于显著性水平，则决策为否定原假设并得出数据不服从正态分布的结论。
P 值 > α：您无法得出数据不服从正态分布的结论（无法否定 H0）
如果 p 值大于显著性水平，则决策为无法否定原假设。您没有足够的证据得出数据不服从正态分布的结论。
主要结果：P 值
在这些结果中，原假设声明数据服从正态分布。由于 p 值为 0.463（大于显著性水平 0.05），则所做的决定为无法否定原假设。您无法得出数据不服从正态分布的结论。
步骤 2：对正态分布的拟合程度进行可视化处理
为了可视化正态分布的拟合，请检查概率图并评估数据点与拟合的分布线的服从程度。正常分布趋于紧密服从直线。偏斜数据将形成曲线。
右偏斜数据
左偏斜数据
提示
在 Minitab 中，将鼠标指针移到拟合分布线上并按住将可看到百分位数和值的控制图。
在这个概率图中，数据沿着正态分布线构成的线条大致为直线。正态分布似乎能够很好地拟合数据。
这篇关于MiniTab的正态性检验结果的分析的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
