本文主要是介绍代码随想录算法训练营第三十天|总结、332.重新安排行程、51.N皇后、37.解数独，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
代码随想录 (programmercarl.com)
总结
332.重新安排行程
欧拉通路和欧拉回路：
欧拉通路：对于图G来说，如果存在一条通路包含G的所有边，则该通路称为欧拉通路，也称欧拉路径。
欧拉回路：如果欧拉路径是一条回路，那么称其为欧拉回路。
欧拉图：含有欧拉回路的图是欧拉图。
题目中说必然存在一条有效路径，所以至少是半欧拉图，也可以是欧拉图。
深度优先搜索（DFS）：
对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次。
遍历欧拉图——Hierholzier算法
主要步骤：从一个可能的起点出发，进行深度优先搜索，但是每次沿着辅助边从每个顶点移动到另外一个顶点的时候，都需要删除这个辅助边。如果没有可移动的路径，则将所在节点加入到栈中（先进后出==所以后面步骤4需要逆序输入），并返回。
算法思路：
1）任选一点为起始点，并记录；
2）从起点出发到达任意一个邻接点，新到达的点成为新的起点，删除经过的边，删除孤立点，记录经过的点；
3）重复步骤2直至回到初始点，此时到达步骤1，将本次记录的点和上次记录的点集合拼接。若本图成为空图，到达步骤4；
4）逆序输出所有记录点。
只有入度与出度差为 1 的节点会导致死胡同
====代码待更新====
51.N皇后
皇后们的约束条件：
- 不能同行
- 不能同列
- 不能同斜线
棋盘的宽度就是for循环的长度，递归的深度就是棋盘的高度，这样就可以套进回溯法的模板里了。
回溯算法主体里面需要放一个判断是否可以防止皇后Q的判断函数
其中对于不能同斜线，需要判断45°和135°，分别如下两种情况：
| i - 2, j - 2 | ||
| i - 1, j - 1 | ||
| i, j |
| i - 2, j + 2 | ||
| i - 1, j + 1 | ||
| i, j |
Java中ArrayList与LinkedList的区别 - 知乎 (zhihu.com)
https://zhuanlan.zhihu.com/p/33141246补充一点ArrayList和LinkedList的区别：
1、ArrayList的实现是基于数组，LinkedList的实现是基于双向链表。
2、对于随机访问，ArrayList优于LinkedList
3、对于插入和删除操作，LinkedList优于ArrayList
4、LinkedList比ArrayList更占内存，因为LinkedList的节点除了存储数据，还存储了两个引用，一个指向前一个元素，一个指向后一个元素。
class Solution {List<List<String>> res = new ArrayList<>();//需要在一开始就声明，因为后面res.add(Array2List(chessboard));会用到public List<List<String>> solveNQueens(int n) {//初始化所有棋盘格为.char[][] chessboard = new char[n][n];//注意此处的棋盘里面放的都是字符，所以需要定义为char类型的数组for (char[] c : chessboard) {Arrays.fill(c, '.');}backtracking(n, 0, chessboard);return res;}public void backtracking(int n, int row, char[][] chessboard){//n表示该棋盘格的规格大小，row表示当前遍历到的行数if (row == n){//表示递归终止条件，开始收集结果res.add(Array2List(chessboard));return;}for (int col = 0; col < n; col++) {if (isValid(n, row, col, chessboard)){chessboard[row][col] = 'Q';backtracking(n, row + 1, chessboard);chessboard[row][col] = '.';//回溯回去}}}public List Array2List(char[][] chessboard){//表示将数组类型的结果转为所需要的list的集合形式List<String> list = new ArrayList<>();for (char[] c : chessboard) {list.add(String.copyValueOf(c));}return list;}public boolean isValid(int n, int row, int col, char[][] chessboard){//以下操作相当于剪枝，即如果有违反题目要求的情况出现，直接就不进行回溯，减少进入递归的次数//检查列，以为此时调用该方法是固定列，这时遍历行去检查列，改变col去检查行for (int i = 0; i < row; i++) {if (chessboard[i][col] == 'Q'){return false;}}//检查45°斜线for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {if (chessboard[i][j] == 'Q'){return false;}}//检查135°斜线for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {if (chessboard[i][j] == 'Q'){return false;}}return true;}
}37.解数独
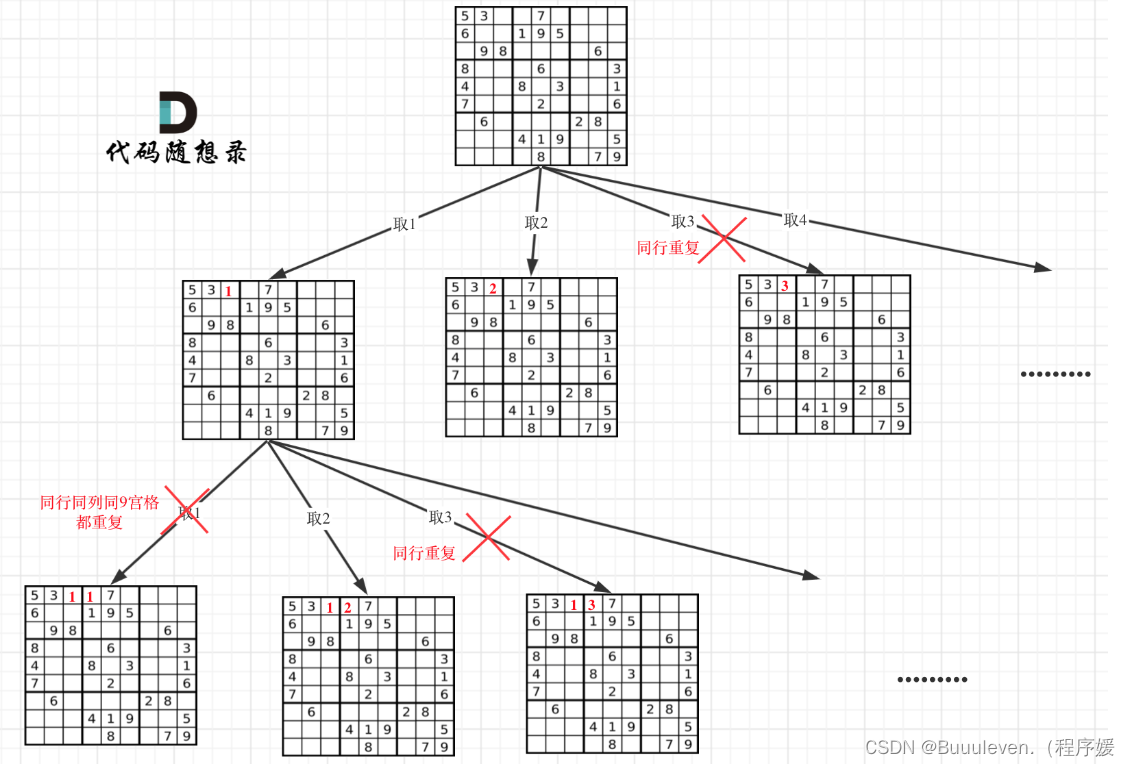
class Solution {public void solveSudoku(char[][] board) {//没有new新的数组，直接修改原来传入的数组，所以返回值为voidbacktracking(board);}public boolean backtracking(char[][] board){//不需要终止条件，因为一旦该数独没有解，会直接返回false，不会陷入死循环//一个for循环遍历棋盘的行，一个for循环遍历棋盘的列，//一行一列确定下来之后，递归遍历这个位置放9个数字的可能性！for (int i = 0; i < 9; i++) {for (int j = 0; j < 9; j++) {if (board[i][j] != '.'){continue;//题目中初始的数独中，空白部分是.，此操作是为了跳过数独中的原始数字}for (char k = '1'; k <= '9'; k++) {if (isValid(i, j, k, board)){board[i][j] = k;if (backtracking((board))){// 如果找到合适一组立刻返回return true;}board[i][j] = '.';}}return false;// 因为如果一行一列确定下来了，这里尝试了9个数都不行，说明这个棋盘找不到解决数独问题的解！// 那么会直接返回，这也就是为什么没有终止条件也不会永远填不满棋盘而无限递归下去！}}// 遍历完没有返回false，说明找到了合适棋盘位置了return true;}public boolean isValid(int row, int col, char val, char[][] board){//检查同一行是否有重复for (int j = 0; j < 9; j++) {if (board[row][j] == val){return false;}}//检查同一列是否有重复for (int i = 0; i < 9; i++) {if (board[i][col] == val){return false;}}//检查同一个九宫格是否有重复int startRow = (row / 3) * 3;int startCol = (col / 3) * 3;for (int i = startRow; i < startRow + 3; i++) {for (int j = startCol; j < startCol + 3; j++) {if (board[i][j] == val){return false;}}}return true;}
}这篇关于代码随想录算法训练营第三十天|总结、332.重新安排行程、51.N皇后、37.解数独的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
