本文主要是介绍LeGO-LOAM 几个特有函数的分析(2),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
接上回LeGO-LOAM 几个特有函数的分析(1)
二、广度优先遍历
广度优先遍历(Breadth-First Search, BFS)是一种用于遍历或搜索树或图的算法。这种算法从树的根(或图的某一指定节点)开始,然后探索邻近的节点,之后对每一个邻近的节点,它再去探索它们各自相邻的节点,这个过程持续进行直到访问所有可达的节点。
广度优先遍历的主要特点是它按照距离起始点的“层次”来遍历。首先访问距离起点最近的节点,然后是它们的邻居,如此类推。
2.1 广度优先遍历的步骤:
-
初始化:首先将起始节点放入队列中。
-
遍历:
- 从队列中弹出一个节点。
- 检查该节点是否为目标节点。如果是,则完成搜索。
- 将该节点的所有未访问过的邻居节点加入队列。
-
重复:重复步骤2,直到队列为空或找到目标节点。
-
结束:当队列为空且目标未找到,或已找到目标节点时,算法结束。
2.2基于 BFS 的点云聚类和外点剔除
2.2.1原理


2.2.2源码注释
void labelComponents(int row, int col){// use std::queue std::vector std::deque will slow the program down greatly// 声明所需的变量,输入的ROW和col是单帧点云第几行第几列的点// 用于存储距离和角度计算的临时变量float d1, d2, alpha, angle;// 用于存储索引的变量int fromIndX, fromIndY, thisIndX, thisIndY;// 标记是否每个扫描线都至少有一个点被添加bool lineCountFlag[N_SCAN] = {false};//用两个数组分别保存x,yqueueIndX[0] = row;queueIndY[0] = col;//算法标志int queueSize = 1;// 队列开始的索引int queueStartInd = 0;// 队列结束的索引int queueEndInd = 1;// 初始化聚类数组allPushedIndX[0] = row;allPushedIndY[0] = col;//计数int allPushedIndSize = 1;//很巧妙,有有效邻点就加一,每次循环减1,实现bfs广度优先遍历关键while(queueSize > 0){// Pop point// 取出当前点x,y坐标fromIndX = queueIndX[queueStartInd];fromIndY = queueIndY[queueStartInd];//队列大小减一--queueSize;//索引加一++queueStartInd;// Mark popped point// 标记该点为一类,聚类就是给点加标签,标签一致的就是一类labelMat.at<int>(fromIndX, fromIndY) = labelCount;// Loop through all the neighboring grids of popped grid// 检查所有邻点for (auto iter = neighborIterator.begin(); iter != neighborIterator.end(); ++iter){// new index// 计算邻点的索引,其实就是上下左右四个点thisIndX = fromIndX + (*iter).first;thisIndY = fromIndY + (*iter).second;// index should be within the boundary// 如果raw为0或者15,上或者下没有邻点,跳过if (thisIndX < 0 || thisIndX >= N_SCAN)continue;// at range image margin (left or right side)//设置矩阵最两边的点也为邻点,因为VLP16是360度//在cow为0时左边的邻点,在1799if (thisIndY < 0)thisIndY = Horizon_SCAN - 1;//在cow为1799时左边的邻点,在0if (thisIndY >= Horizon_SCAN)thisIndY = 0;// prevent infinite loop (caused by put already examined point back)// 如果该点已被标记,则跳过if (labelMat.at<int>(thisIndX, thisIndY) != 0)continue;// 计算角度差以决定是否将邻点加入到当前区域// 距离雷达远的是D1,近的是D2d1 = std::max(rangeMat.at<float>(fromIndX, fromIndY),rangeMat.at<float>(thisIndX, thisIndY));d2 = std::min(rangeMat.at<float>(fromIndX, fromIndY), rangeMat.at<float>(thisIndX, thisIndY));//(0,-1),(0,1),意味着是一条线上的点,角度是360/1800*3.14/180=0.0035if ((*iter).first == 0)alpha = segmentAlphaX;else//(1,0),(-1,0),意味着是上下两条线上的点,角度是30/(16-1)*3.14/180=0.035alpha = segmentAlphaY;//计算图中angle角度angle = atan2(d2*sin(alpha), (d1 -d2*cos(alpha)));//如果角度大于60度if (angle > segmentTheta){//把此邻点放入队列queueIndX[queueEndInd] = thisIndX;queueIndY[queueEndInd] = thisIndY;//增加size++queueSize;//末尾索引右移++queueEndInd;//把此邻点赋上和之前取出来的点一样的标签labelMat.at<int>(thisIndX, thisIndY) = labelCount;//这行有点被标记过lineCountFlag[thisIndX] = true;//保存聚类结果allPushedIndX[allPushedIndSize] = thisIndX;allPushedIndY[allPushedIndSize] = thisIndY;++allPushedIndSize;}}}// check if this segment is validbool feasibleSegment = false;//如果聚类大于30则认为是一个好的聚类if (allPushedIndSize >= 30)feasibleSegment = true;//如果大于5,而且都是竖着的超过3个,也认为是一个好聚类,可能是树,电线杆else if (allPushedIndSize >= segmentValidPointNum){int lineCount = 0;for (size_t i = 0; i < N_SCAN; ++i)if (lineCountFlag[i] == true)++lineCount;if (lineCount >= segmentValidLineNum)feasibleSegment = true; }// segment is valid, mark these points//如果聚类成功,标签加一if (feasibleSegment == true){++labelCount;}else{ // segment is invalid, mark these pointsfor (size_t i = 0; i < allPushedIndSize; ++i){//不成功,则标记为999999,代表依托答辩labelMat.at<int>(allPushedIndX[i], allPushedIndY[i]) = 999999;}}}需要注意的点:
一是 邻点的定义,就是代表取当前点上下左右四个点
std::pair<int8_t, int8_t> neighbor; neighbor.first = -1; neighbor.second = 0; neighborIterator.push_back(neighbor); neighbor.first = 0; neighbor.second = 1; neighborIterator.push_back(neighbor); neighbor.first = 0; neighbor.second = -1; neighborIterator.push_back(neighbor); neighbor.first = 1; neighbor.second = 0; neighborIterator.push_back(neighbor);
二是 巧妙的通过queueSize 实现广度优先遍历算法的核心
开始是int queueSize =1,让其进入循环
while(queueSize > 0){//队列大小减一--queueSize;for (auto iter = neighborIterator.begin(); iter != neighborIterator.end(); ++iter){//如果角度大于60度if (angle > segmentTheta){//增加size++queueSize;}}
}
三是 聚类时候,大于30个点,或者大于5个点,但是有三个竖着的聚为一类
我觉得原因是考虑到竖着的点距离远的因素
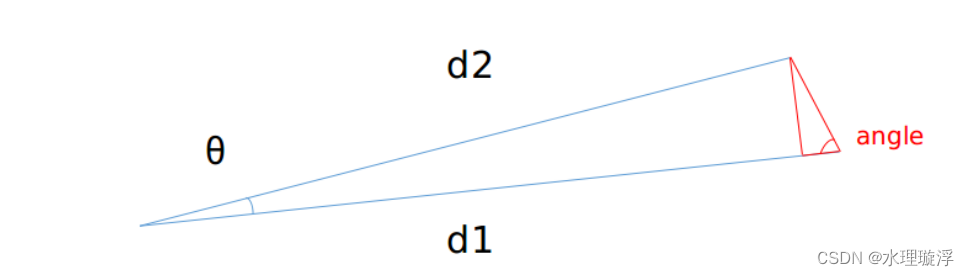
四是 通过计算角度来判断是否是邻点
想象一下,是不是D1越长,angle越小
2.3函数的调用
用此种方式实现了一帧雷达所有点的聚类
for (size_t i = 0; i < N_SCAN; ++i)for (size_t j = 0; j < Horizon_SCAN; ++j)//上一个函数说过地面点label被置为1 //如果这个点既不是地面点也没有聚类过,开始聚类if (labelMat.at<int>(i,j) == 0)labelComponents(i, j);这篇关于LeGO-LOAM 几个特有函数的分析(2)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





