二叉排序树（BST）/二叉查找树的建立(BST是笔试面试的常客)

本文主要是介绍二叉排序树（BST）/二叉查找树的建立(BST是笔试面试的常客)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

分享一下我老师大神的人工智能教程！零基础，通俗易懂！http://blog.csdn.net/jiangjunshow

也欢迎大家转载本篇文章。分享知识，造福人民，实现我们中华民族伟大复兴！

二叉排序树又叫二叉查找树，英文名称是：Binary Sort Tree. BST的定义就不详细说了，我用一句话概括：左 < 中 < 右。根据这个原理，我们可以推断：BST的中序遍历必定是严格递增的。

在建立一个BST之前，大家可以做一下这个题目（很简单的）：

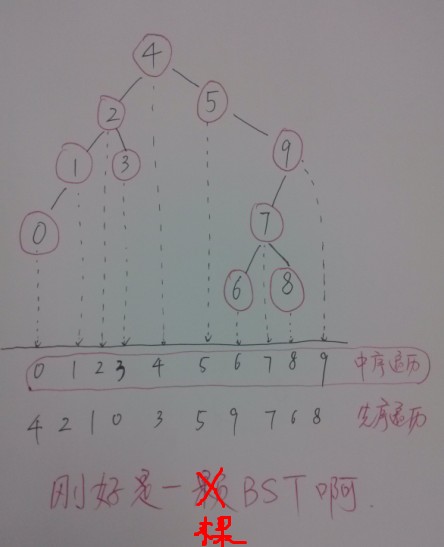
已知，某树的先序遍历为：4, 2, 1 ,0, 3, 5, 9, 7, 6, 8. 中序遍历为: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. 请画出该树。

我们知道，树的基本遍历有4种方式，分别是：

先序遍历；中序遍历；后续遍历；层次遍历。事实上，知道任意两种方式，并不能唯一地确定树的结构，但是，只要知道中序遍历和另外任意一种遍历方式，就一定可以唯一地确定一棵树，于是，上面那个题目的答案如下：

下面，我们来看看BST的建立过程，程序如下（没考虑内存泄露）：

#include <iostream>using namespace std;// BST的结点typedef struct node{ int key; struct node *lChild, *rChild;}Node, *BST;// 在给定的BST中插入结点，其数据域为element, 使之称为新的BSTbool BSTInsert(Node * &p, int element){ if(NULL == p) // 空树 {  p = new Node;  p->key = element;  p->lChild = p->rChild = NULL;  return true; } if(element == p->key) // BST中不能有相等的值  return false; if(element < p->key)  // 递归  return BSTInsert(p->lChild, element); return BSTInsert(p->rChild, element); // 递归}// 建立BSTvoid createBST(Node * &T, int a[], int n){ T = NULL;  int i; for(i = 0; i < n; i++) {  BSTInsert(T, a[i]); }}// 先序遍历void preOrderTraverse(BST T){ if(T) {  cout << T->key << " ";  preOrderTraverse(T->lChild);  preOrderTraverse(T->rChild); }}// 中序遍历void inOrderTraverse(BST T){ if(T) {  inOrderTraverse(T->lChild);  cout << T->key << " ";  inOrderTraverse(T->rChild); }}int main(){ int a[10] = {4, 5, 2, 1, 0, 9, 3, 7, 6, 8}; int n = 10; BST T; // 并非所有的a[]都能构造出BST,所以，最好对createBST的返回值进行判断 createBST(T, a, n); preOrderTraverse(T); cout << endl; inOrderTraverse(T); cout << endl; return 0;}

那么，怎么知道我们这个程序对不对呢？我们输出其先序和中序遍历，这样就可以完全确定这棵树，运行程序，发现先序遍历为：4, 2, 1 ,0, 3, 5, 9, 7, 6, 8. 中序遍历为: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. 好了，这棵树确定了，如上图（已画），那棵树真的是一棵BST, 真的。在后续的博文中，我们会给出二叉排序树的判定方法，期待ing.