学习理论、模型选择、特征选择——斯坦福CS229机器学习个人总结（四）

本文主要是介绍学习理论、模型选择、特征选择——斯坦福CS229机器学习个人总结（四），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

这一份总结里的主要内容不是算法，是关于如何对偏差和方差进行权衡、如何选择模型、如何选择特征的内容，通过这些可以在实际中对问题进行更好地选择与修改模型。

1、学习理论（Learning theory）

1.1、偏差/方差（Bias/variance）

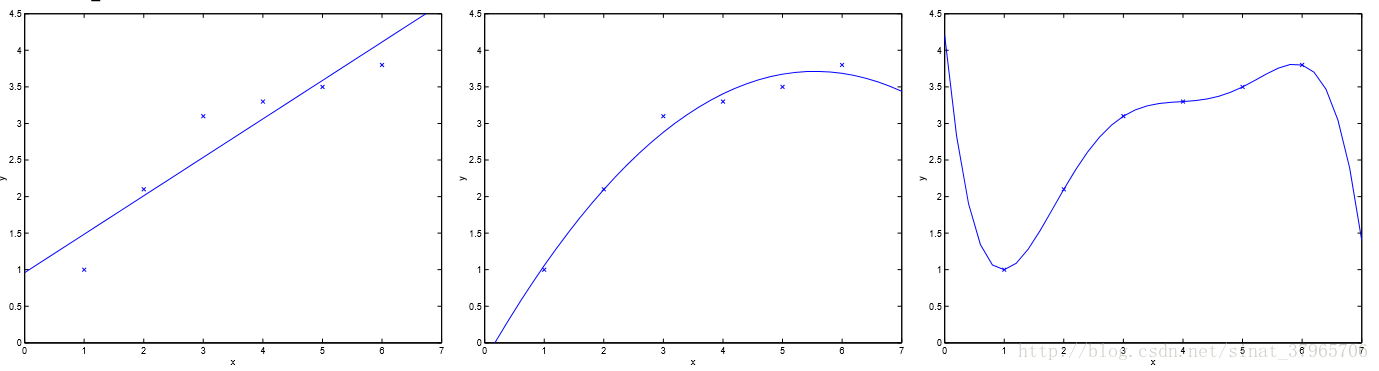
图一
对一个理想的模型来说，它不关心对训练集合的准确度，而是更关心对从未出现过的全新的测试集进行测试时的性能，即泛化能力（Generalization ability）。
有的模型用在用一个样本集训练过后，再用同一个样本集做预测，这样得到的模型的准确率非常高。但是，当用这个模型去预测新的数据的时候，效果却非常不理想。这就是泛化能力弱的表现，这样的模型非常容易过拟合。

图一最左边的图，用线性模型去拟合一个二次模型，无论该训练集中有多少样本，都会不可避免地出现较大的误差，这种情况被称为欠拟合，对应着高偏差；
图一最右边的图，用高次模型去拟合一个二次模型，虽然它能够让图中每个样本点都经过该曲线，但是对于新来的数据可能会强加上一些它们并不拥有的特性（一般是训练样本带来的），这会让模型非常的敏感，这种情况被称为过拟合，对应着高方差。

如何选择一个模型使得它在偏差与方差之间取得一个平衡，是学习理论要解决的问题。在下面“一致收敛的推论”一节中，会得到一个用来权衡偏差、方差的公式，接下来会从头开始推导这个公式。

1.2、准备知识

开始推导之前要先把一些准备知识提出来，这样从“一致收敛”中开始的推导会很顺利。

联合界引理（The union bound）

引理：令$A_1,A_2,\cdots,A_k$是k个事件，组合成k集，它们可能相互独立，也可能步相互独立，对此，我们有：

$$P(A_1\cup\cdots\cup A_k)\leq P(A_1)+\cdots+P(A_k)\tag{1}$$
它要表达的意思是“K集事件之一发生的概率最多是K集发生的概率之和”。
比如当 $P(A_1\cup\cdots\cup A_k)=P(A_1)$，它的概率最多是K集发生的概率之和。

霍夫丁不等式（Hoeffding inequality）

引理：令$Z_1,Z_2\cdots,Z_m$为m个独立同分布事件，它们都服从伯努利分布，则有:

$$P(Z_i=1)=\phi,P(Z_i=0)=1-\phi$$
并用 $Z_i$的平均值来得到一个 $\phi$的估计值 $\hat{\phi}$：
$$\hat{\phi}=\frac{\sum_{i=1}^mZ_i}{m}\tag{2}$$
接着对于任意的固定值 $\gamma>0$，存在：
$$P(\left|\phi-\hat{\phi} \right|>\gamma)\leq2\exp(-2\gamma^2m)\tag{3}$$
以上就是霍夫丁不等式，也称为切尔诺夫界（Chernoff bound）。
这个定理的意义在于，随着 $m$的增长，右式的指数会持续下降，左式中对参数 $\hat{\phi}$的估计会越来越接近真实值 $\phi$（画个 $e^{-x}$的图像就知道了）。

经验风险最小化（Empirical risk minimization）

下面以二分类问题进行说明。
给定一个训练集$S\begin{Bmatrix} (x^{(i)},y^{(i)});i=1,2,\cdots,m \end{Bmatrix}$，$(x^{(i)},y^{(i)})$是服从概率分布$D$的独立同分布变量，那么对于一个假设$h$，我们将假设$h$的训练误差（Training error）——也称为经验风险（Empirical risk）或者是经验误差（Empirical error）——定义为：

$$\hat{\varepsilon}=\frac{1}{m}\sum_{i=1}^mI\begin{Bmatrix} h(x^{(i)}) \neq y^{(i)}\end{Bmatrix}\tag{4}$$
它表示：在训练样本中，用假设 $h$进行分类，分类失败数占总数的百分比。注意它在表示上 有带帽符号。

相对应的有一般风险，也称为一般误差（Generalization error）：

$$\varepsilon=P_D(h(x)\neq y)\tag{5}$$
$P_D$表示 $(x,y)$服从 $D$分布。
式（5）表示：实际分类中，使用了假设 $h$进行分类，样本不服从 $D$分布的概率。它在表示上 无带帽符号。

在我的理解中，训练误差是训练中产生的误差，一般误差是实际预测、分类中产生的误差。接下来的推导中它们会一直出现，可能会搞混，要一直理解到它们的意思才行。

假设模型集合为：

$$H=\begin{Bmatrix} h_\theta:h_\theta(x)=I\begin{Bmatrix} \theta^Tx\geq0 \end{Bmatrix},\theta\in R^{n+1} \end{Bmatrix}\tag{6}$$
集合 $H$中，每一个成员都是一个假设函数 $h$，且它们都是线性分类器。

由式（4）经验风险的形式化定义，有经验风险最小化（简称ERM）为：

$$\theta=\arg\min_\theta\hat{\varepsilon}(h_\theta)\tag{7}$$
它表示：选择一个参数 $\theta$，它所对应的假设函数 $h$，使得经验风险最小。

还有另外一种ERM的等价表示方法，其ERM的定义为：

$$\hat{h}=\arg\min_{h\in H}\hat{\varepsilon}(h)\tag{8}$$

它表示：选择一个假设函数$h$，使得经验风险最小。

1.3、一致收敛（Uniform convergence）

此处的一致收敛有两个前提。一是由第二种ERM推导，二是式（6）中假设函数的数量是有限的情况下的。
一致收敛的意义是：训练误差与一般误差的差值大于某阈值的概率存在着上界。还有一点扩展就是这个上界会因样本数量的上升而急速下降。由一致收敛我们可以推导出偏差/方差权衡的方式。

首先，假设类的集合H={h1,h2,⋯,hk<

这篇关于学习理论、模型选择、特征选择——斯坦福CS229机器学习个人总结（四）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---