[最优化导论]C6 集合约束和无约束优化问题

集合约束和无约束优化问题

集合约束和无约束优化的基本形式为：

$\begin{array}{r}minimizef(\mathbf{x})\\ subjectto\mathbf{x}\in \Omega \end{array}$

目标就是在约束集$\Omega$中找出最好的决策变量$\mathbf{x}$，如果$\Omega ={\mathbb{R}}^n$，则问题就会转化为无约束优化问题。

用数学化的形式定义一下局部最小点就是：

如果存在一个$\epsilon >0$，对于所有满足$||\mathbf{x}-{\mathbf{x}}^{\ast }||<\epsilon$的向量$\mathbf{x}$，不等式$f(\mathbf{x})\ge f({\mathbf{x}}^{\ast })$都成立，则称${\mathbf{x}}^{\ast }$是函数$f$在定义域中的一个局部最小点。

说的简单点就是如果在${\mathbf{x}}^{\ast }$一个邻域内的函数值都比在这个点大，则这个点就是局部最小点。

如果把上述的$\ge$换成$>$，局部最小点也就成严格局部最小点。

优化问题的极小点可能位于约束集$\Omega$的内部，也可能位于边界上。处于边界上的极小点需要满足一定条件之后才能成为真正的极小点。

举个例子：对于$f(x)=x^3$的函数，毫无疑问该函数是单调递增的，但一阶导数和二阶导数在原点的值为0，显然x=0并不是极小值点，由此可以看出成为局部最小点需要满足一些必要条件和充分条件，在多维空间中也是如此。

n元实值函数求导问题回顾：

导数矩阵（雅克比矩阵）为：$Df(x_0)=[\frac{\partial f}{\partial x_1}(x_0)\cdots \frac{\partial f}{\partial x_n}(x_0)]$

如果函数f为一个向量，并且它的作用是将n维空间转化为m为空间，则对应的矩阵为：

$Df(x_0)=[\frac{\partial f}{\partial x_1}(x_0)\cdots \frac{\partial f}{\partial x_n}(x_0)]=\left[\begin{array}{ccc}\frac{\partial f_1}{\partial x_1}(x_0)& \cdots & \frac{\partial f_1}{\partial x_n}(x_0)\\ \cdots & & \cdots \\ \frac{\partial f_m}{\partial x_1}(x_0)& \cdots & \frac{\partial f_m}{\partial x_n}(x_0)\end{array}\right]$

如果二次可微，则对应的黑塞矩阵为：

$\mathbf{F}(\mathbf{x})\triangleq D^{2}f=\left[\begin{array}{cccc}\frac{{\partial }^{2}f}{\partial x_1^2}& \frac{{\partial }^{2}f}{\partial x_2\partial x_1}& \cdots & \frac{{\partial }^{2}f}{\partial x_n\partial x_1}\\ \frac{{\partial }^{2}f}{\partial x_1\partial x_2}& \frac{{\partial }^{2}f}{\partial x_2^2}& \cdots & \frac{{\partial }^{2}f}{\partial x_n\partial x_2}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{{\partial }^{2}f}{\partial x_1\partial x_n}& \frac{{\partial }^{2}f}{\partial x_2\partial x_n}& \cdots & \frac{{\partial }^{2}f}{\partial x_n^2}\end{array}\right]$

1.一阶必要条件

首先来看这样一种情况，

在上图中，如果x向量往d2方向走一小步，就会走出约束集合；而往d1方向走一小步还在约束集内，所以d1为可行方向。对应的，d2为不可行方向。

设在约束集内的可行方向为$\mathbf{d}$，函数对应的梯度为$▽f(\mathbf{x})$为函数梯度，则沿着可行方向的方向倒数为梯度与单位可行方向向量的内积。

对应的一阶必要条件为：

$f$在约束集$\Omega$上一阶连续可微，如果${\mathbf{x}}^{\ast }$是函数$f$在约束集$\Omega$上局部极小点，则需要满足处于${\mathbf{x}}^{\ast }$的任意可行方向上，都有：

${\mathbf{d}}^T▽f(\mathbf{x})\ge 0$

成立。

例如在下图中，x1并不能满足一阶必要条件，而x2可以。所以x1不是局部极小点。

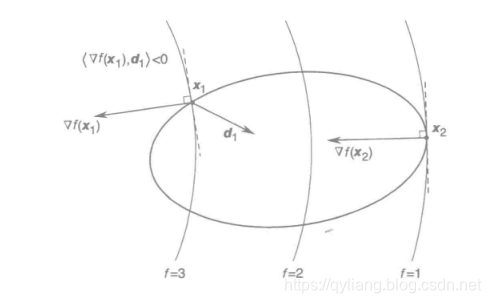
推论

如果${\mathbf{x}}^{\ast }$是位于约束集内部的点，则需要满足的一阶必要条件为：

$▽f({\mathbf{x}}^{\ast })=0$

即需要满足梯度为0向量，相当于在一元函数中函数的导数为0是必要条件。

2. 二阶必要条件

一阶必要条件并不能确保某个点为局部最小点，局部最小点还需要满足的二阶必要条件为：

$\Omega$上二阶连续可微，满足一阶必要条件的情况下，还需满足：

$${\mathbf{d}}^T\mathbf{F}({\mathbf{x}}^{\ast })\mathbf{d}\ge 0$$

其中$\mathbf{F}$为函数对应的黑塞矩阵。

同样如果${\mathbf{x}}^{\ast }$在约束集内部时，需要满足的二阶必要条件为：

$$▽f({\mathbf{x}}^{\ast })=0$$

$${\mathbf{d}}^T\mathbf{F}({\mathbf{x}}^{\ast })\mathbf{d}\ge 0$$

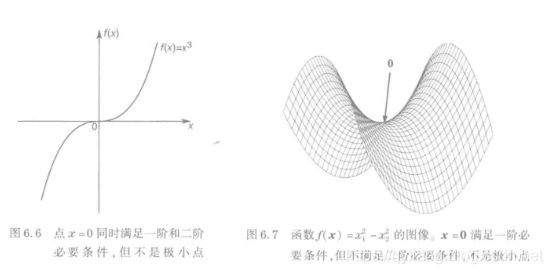
同时满足两个必要条件也不一定为局部最小点，如作图；右图为满足一阶必要条件，而不满足二阶必要条件的例子。

3. 局部最小点的充分条件

如果：

1. $▽f({\mathbf{x}}^{\ast })=0$
2. $\mathbf{F}({\mathbf{x}}^{\ast })>0$

则${\mathbf{x}}^{\ast }$为函数$f$的严格局部最小点。

相当于在一元函数中，一阶导数为0且二阶导数大于0，则该点为极小值。

当然面对一个高度非线性的问题，如果利用二阶必要条件或充分条件求解，需要很多次进行二阶求导，具有很大的工作量，所以通常采用极小值的迭代求解方法，下一章将会介绍。