DataWhale-(scikit-learn教程)-Task06(主成分分析)-202112

本文主要是介绍DataWhale-(scikit-learn教程)-Task06(主成分分析)-202112，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、 PCA主成分分析算法介绍

在这里插入图片描述

二、算法实现

import sys
from pathlib import Path
curr_path = str(Path().absolute()) # 当前文件所在绝对路径
parent_path = str(Path().absolute().parent) # 父路径
sys.path.append(parent_path) # 添加路径到系统路径from Mnist.load_data import load_local_mnistfrom sklearn.decomposition import PCA
import numpy as np
import matplotlib.pyplot as plt(X_train, y_train), (X_test, y_test) = load_local_mnist(normalize = False,one_hot = False)
m , p = X_train.shape # m：训练集数量，p：特征维度数print(f"原本特征维度数：{p}") # 特征维度数为784# n_components是>=1的整数时，表示期望PCA降维后的特征维度数
# n_components是[0,1]的数时，表示主成分的方差和所占的最小比例阈值，PCA类自己去根据样本特征方差来决定降维到的维度
model = PCA(n_components=0.95) 
lower_dimensional_data = model.fit_transform(X_train)print(f"降维后的特征维度数：{model.n_components_}")

approximation = model.inverse_transform(lower_dimensional_data) # 降维后的数据还原
plt.figure(figsize=(8,4));# 原始图片
plt.subplot(1, 2, 1);
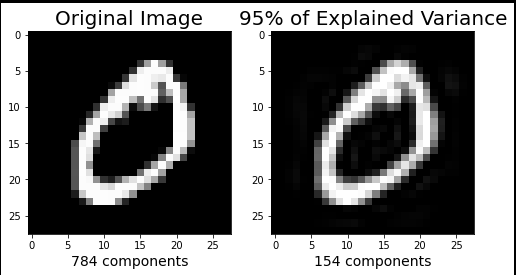
plt.imshow(X_train[1].reshape(28,28),cmap = plt.cm.gray, interpolation='nearest',clim=(0, 255));
plt.xlabel(f'{X_train.shape[1]} components', fontsize = 14)
plt.title('Original Image', fontsize = 20)
# 降维后的图片
plt.subplot(1, 2, 2);
plt.imshow(approximation[1].reshape(28, 28),cmap = plt.cm.gray, interpolation='nearest',clim=(0, 255));
plt.xlabel(f'{model.n_components_} components', fontsize = 14)
plt.title('95% of Explained Variance', fontsize = 20)
plt.show()

在这里插入图片描述

model = PCA() # 这里需要分析所有主成分，所以不降维
model.fit(X_train)
tot = sum(model.explained_variance_) 
var_exp = [(i/tot)*100 for i in sorted(model.explained_variance_, reverse=True)] 
cum_var_exp = np.cumsum(var_exp)
plt.figure(figsize=(10, 5))
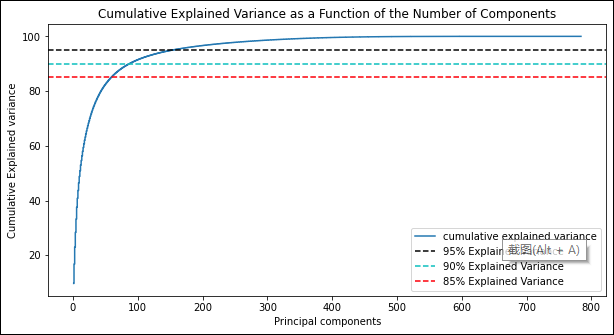
plt.step(range(1, p+1), cum_var_exp, where='mid',label='cumulative explained variance') # p：特征维度数
plt.title('Cumulative Explained Variance as a Function of the Number of Components')
plt.ylabel('Cumulative Explained variance')
plt.xlabel('Principal components')
plt.axhline(y = 95, color='k', linestyle='--', label = '95% Explained Variance')
plt.axhline(y = 90, color='c', linestyle='--', label = '90% Explained Variance')
plt.axhline(y = 85, color='r', linestyle='--', label = '85% Explained Variance')
plt.legend(loc='best')
plt.show()

在这里插入图片描述

def explained_variance(percentage, images): ''':param: percentage [float]: 降维的百分比:return: approx_original: 降维后还原的图片:return: model.n_components_: 降维后的主成分个数'''   model = PCA(percentage)model.fit(images)components = model.transform(images)approx_original = model.inverse_transform(components)return approx_original,model.n_components_
plt.figure(figsize=(8,10));
percentages = [1,0.99,0.95,0.90]
for i in range(1,5):plt.subplot(2,2,i)im, n_components = explained_variance(percentages[i-1], X_train)im = im[5].reshape(28, 28) # 重建成图片plt.imshow(im,cmap = plt.cm.gray, interpolation='nearest',clim=(0, 255))plt.xlabel(f'{n_components} Components', fontsize = 12)if i==1:plt.title('Original Image', fontsize = 14)else:plt.title(f'{percentages[i-1]*100}% of Explained Variance', fontsize = 14)
plt.show()