统计学习方法——逻辑斯蒂回归与最大熵模型

本文主要是介绍统计学习方法——逻辑斯蒂回归与最大熵模型，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

逻辑斯蒂回归（LR）是统计学习中的经典分类方法。最大熵是概率模型学习的一个准则，将其推广到分类问题得到最大熵模型。逻辑斯蒂回归模型与最大熵模型都属于对数线性模型。

1、逻辑斯蒂回归模型

线性回归与逻辑回归关系：

在学习逻辑回归时，常常会联想到线性回归。线性回归一般预测解决连续值预测的问题，对已有的数据进行线性拟合，运用最小二乘法等，找到最佳拟合曲线，然后得到线性模型，来进行预测，是一个线性模型。而逻辑回归时一个非线性模型，sigmoid函数，又称逻辑回归函数。用于解决分类问题，输出某个类别的概率。如果把逻辑回归拆开，其本质也是线性回归模型。因为除了sigmoid映射函数外，其他步骤都是线性回归。sigmoid能轻松出列0、1分类问题。

逻辑斯蒂回归模型定义及来源

（1）一阶逻辑斯蒂回归

逻辑斯蒂回归模型主要是来源于逻辑斯蒂分布与逻辑斯蒂函数。当然，如果换一个名字，你对它应当相当熟悉，那就是sigmoid函数。它的形式如下：

$f(x) = \frac{1}{1+e^{-x}}$

而逻辑斯蒂回归模型的另一个则来源于线性回归：

把两者组合起来，就形成了大名鼎鼎的十大数据挖掘算法（LR）：

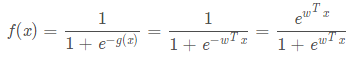
f(x)的值是一个0到1之间的数。

（2）二项逻辑斯蒂回归模型

二项回归模型是如下的条件概率分布：

$P(Y=1|X) = \frac{e^{\omega · x+b}}{1+e^{\omega · x+b}}$

$P(Y=0|X) = \frac{1}{1+e^{\omega · x+b}}$

这里， $x\in R^{n}$ 是输入， $Y\in 0 to 1$ 是输出，w，b是参数，wx是w，x的内积。

在学习逻辑斯蒂回归模型的特点是，要涉及到一个名词“几率”。一个事件的几率是指该时间发生的概率与该事件不发生的概率的比值。如果发生的概率是p，那么，该事件的几率是： $\frac{P}{1-P}$ ,对事件的对数几率或logit函数是

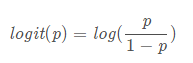
所以，对逻辑斯蒂回归而言，综合可得式子：

这里可以看出，输出y=1的对数几率是输入x的线性函数

（3）模型参数估计

现在大致模型已经知道了，参数未知。只要计算得出模型的参数就可得到具体模型。

这里采用极大似然估计法作为参数估计，把问题变成以似然函数为目标函数的最优化问题

这样，问题就变成了以对数似然函数为目标函数的最优化问题。逻辑斯蒂回归学习中通常采用的方法是梯度下降法及拟牛顿法。

似然函数可以看做是条件概率的逆反

例子：

一枚硬币，已知正反面朝上的概率各自是pH = 0.5。若投两次都正面朝上的概率是0.25，用条件概率表示，就是：

$P(HH | pH = 0.5) = 0.5^{2} = 0.25$ H表示正面朝上

在统计学中，我们关心的是在已知一系列投掷的结果时，关于硬币投掷时正面朝上的可能性的信息。我们可以建立一个统计模型：假设硬币投出时会有pH 的概率正面朝上，而有1 − pH 的概率反面朝上。这时，条件概率可以改写成似然函数：

$L(pH = 0.5|HH ) = P(HH | pH = 0.5) = 0.25$

也就是说，对于取定的似然函数，在观测到两次投掷都是正面朝上时，pH = 0.5 的似然性是0.25（这并不表示当观测到两次正面朝上时pH = 0.5 的概率是0.25）

如果pH=0.6 ，那么似然函数的值也会变化成0.36

注意到似然函数的值变大了。这说明，如果参数pH 的取值变成0.6的话，结果观测到连续两次正面朝上的概率要比假设pH = 0.5时更大。也就是说，参数pH 取成0.6 要比取成0.5 更有说服力，更为“合理”。总之，似然函数的重要性不是它的具体取值，而是当参数变化时函数到底变小还是变大。对同一个似然函数，如果存在一个参数值，使得它的函数值达到最大的话，那么这个值就是最为“合理”的参数值。

在这个例子中，似然函数实际上等于：