管理类联考——数学——真题篇——按题型分类——充分性判断题——蒙猜D

本文主要是介绍管理类联考——数学——真题篇——按题型分类——充分性判断题——蒙猜D，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

先看目录，除了2018年比较怪，其他最多2个D（数学只有两个弟弟，一个大弟，一个小弟）

2023

真题（2023-16）-D

-数据分析-排列组合-组合-C运算

2022

真题（2022-21）-D-分析选项⇒是否等价⇒是，选D

-数列-等比数列-等比中项；勾股定理
21.某直角三角形的三边长 𝑎 , 𝑏 , 𝑐 成等比数列，则能确定公比的值
（1）𝑎 是直角边长
（2）𝑐 是斜边长

2021

真题（2021-21）-D-特值体系法；

D-几何-解析几何-位置-线圆位置-相离-也还是转为圆心点到直线的距离公式
21.设x ，y为实数，则能确定$x\le y$。
（1）$x^2\le y-1$。
（2）$x^2+(y-2{)}^2\le 2$。

真题（2021-25）-D-要素列表法plus-要素间的比；一般而言，完成拼图要确定几个要素与就需要条件匹配几个关系；若只要求几个要素之间的比，则需要的关系个数减1；-D-数列-等差数列和等比数列

25.给定两个直角三角形，则这两个直角三角形相似。
（1）每个直角三角形边长成等比数列。
（2）每个直角三角形边长成等差数列。

2020

真题（2020-21）-D-分析选项⇒是否等价⇒是，选D

-几何-立方几何
21、在长方体中，能确定长方体的体对角线长度。
（1）已知长方体一个顶点的三个面的面积。
（2）已知长方体一个顶点的三个面的面对角线的长度。

2019

真题（2019-17）-D

-数据分析-概率已知事件的概率求概率⟹ 独立事件概型⟹ 乘法计算概率
17、有甲乙两袋奖券，获奖率分别为 p 和q ，某人从两袋中各随机抽取 1 张奖券，则此人获奖的概率不小于$\frac{3}{2}$
(1) 已经$p+q=1$
(2) 已知 $pq=\frac{1}{4}$

真题（2019-20）-D

-代数-方程-整数不定方程
20、关于 x 的方程$x^2+ax+b=1$有实根

(1) $a+b=0$
(2) $a-b=0$

2018

真题（2018-18）-D-要素列表法plus-特殊套路-所有圆半径，球半径，均设为需要通过勾股定理求解；即要确定两个要素，需要两个关系；

-D-代数-方程-出现了两个及以上未知量，而数量关系却少于未知量的个数-整数不定方程-先根据题目转化为ax+by=c形式的不定方程，然后结合整除、倍数和奇偶特征分析讨论求解
18.设$m,n$是正整数，则能确定$m+n$的值。
（1） $\frac{1}{m}+\frac{3}{n}=1$
（2） $\frac{1}{m}+\frac{2}{n}=1$

真题（2018-19）-D

-代数-不等式-均值不等式
19.甲、乙、丙 3 人年收入成等比数列，则能确定乙的年收入最大值。
（1）已知甲丙两人年收入之和。
（2）已知甲丙两人年收入之积。

真题（2018-20）-D-分析选项⇒是否等价⇒是，选D

-几何-平面几何-长方形
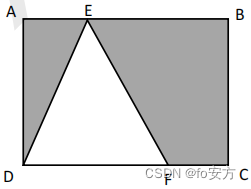
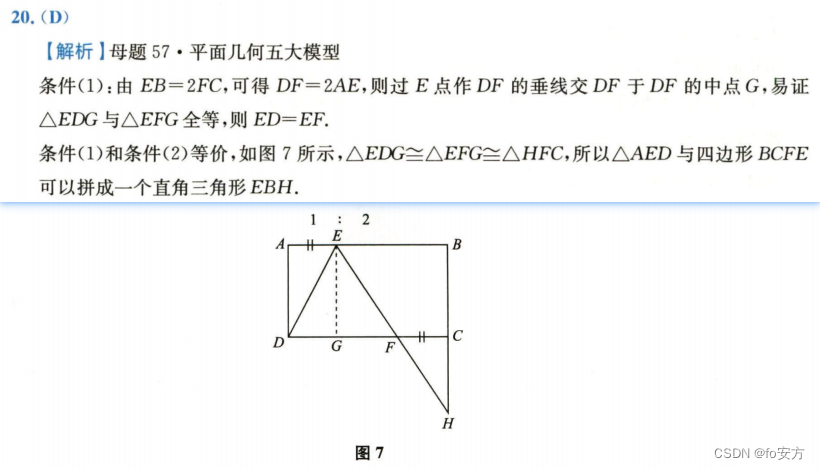
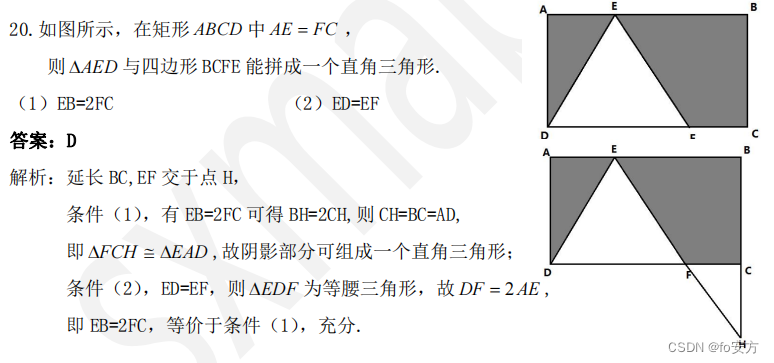
20.如图所示，在矩形ABCD中AE=FC，则三角形AED与四边形 BCFE能拼成一个直角三角形。
（1）EB=2FC
（2）ED=EF

真题（2018-23）-D

-应用题-增长率
23.如果甲公司年终奖总额增加 25%，乙公司年终奖总额减少 10%，两者相等，则能确定两公司的员工人数之比。
（1）甲公司的人均年终奖与乙公司相同。
（2）两公司的员工数之比与两公司年终奖总额之比相等。
D。本题考查比例问题。设甲公司的年终奖总额为a，乙公司的年终奖总额为b，则有a（1+25%）=b（1-10%），简化得两公司年终奖总额之比a/b=18/25，结合条件（1），可得两公司员工人数之比与奖金总额之比相等，故（1）充分，条件（2）显然充分。
秒杀：等价条件题，选项（1）是（2）充分必要条件，都选D。∵（2）甲员工/乙员工=甲年终/乙年终，得：甲年终/甲员工=乙年终/乙员工，得：甲人均年终奖=乙人均年终奖。

真题（2018-25）-D-选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻，相加非全集选D

-函数-复合函数
25.设函数$f(x)=x^2+ax$ ，则 f (x) 最小值与$f(f(x))$的最小值相等。
（1）$a\ge 2$
（2）$a\le 0$

2017

真题（2017-16）-D-分析选项⇒是否等价⇒是，选D

-应用题-工程
16.某人需要处理若干份文件，第一个小时处理了全部文件的 15，第二个小时处理了剩余文件的 14，则此人需要处理的文件共 25 份。
（1）前两小时处理了 10 份文件
（2）第二小时处理了 5 份文件

2016

真题（2016-25）-D-要素列表法plus-特殊套路-一次与二次-大前提有等式+一次条件 vs 二次条件 ⟹ 选D；

-D-代数-方程-一元二次方程-根的分布
25.已知$f(x)=x^2+ax+b$，则$0\le f(1)\le 1$
（1） $f(x)$ 在区间[ 0，1 ]中有两个零点。
（2） $f(x)$ 在区间[ 1，2 ]中有两个零点。

2015

真题（2015-16）-D

-几何-解析几何-直线与圆的位置关系
16.圆盘$x^2+y^2\le 2(x+y)$被直线 L 分成面积相等的两部分。
（1） L：$x+y=2$
（2） L：$2x-y=1$

真题（2015-23）-D

-数列-等差数列-前n项和的最值
23.已知数列{$a_n$}是公差大于零的等差数列，{$S_n$}是{$a_n$}的前n 项和。则$S_n\ge S_{10}，n=1,2,...$
（1）$a_{10}=0$
（2）$a_{11}{a}_{10}＜0$

2014

2013

真题（2013-20）-D-翻译“≥≤”：题干或选项可以翻译为“≥”或“≤”，选D。得：题干“达到0.999”翻译为“≥0.999”，选D。（谁能想到呢。_。）

-数据分析-概率-已知事件的概率求概率⟹ 独立事件概型⟹ 乘法计算概率-独立事件-若干独立事件同时发生的概率，等于这些事件单独发生的概率的乘积=分步乘-
20.档案馆在一个库房安装了n个烟火感应报警器，每个报警器遇到烟火成功报警的概率为$p$。该库房遇烟火发出报警的概率达到$0.999$。
（1） $n=3，p=0.9$
（2） $n=2，p=0.97$

真题（2013-25）-D；-容易误判选A，因为选范围小的，也容易误判选C，因为一个等号+一个不等号！！！！！！

-数列-递推公式-难度升级-中间段才出现周期
25.设$a_1=1,a_2=k,...,a_{n+1}=|a_n-a_{n-1}|,(n\ge 2)$ ，则$a_{100}+a_{101}+a_{102}=2$
（1） $k=2$
（2）k 是小于 20 的正整数

这篇关于管理类联考——数学——真题篇——按题型分类——充分性判断题——蒙猜D的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---