信号与线性系统翻转课堂笔记4——连续LTI系统的微分方程模型与求解

本文主要是介绍信号与线性系统翻转课堂笔记4——连续LTI系统的微分方程模型与求解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

信号与线性系统翻转课堂笔记4——连续LTI系统的微分方程模型与求解

The Flipped Classroom4 of Signals and Linear Systems

对应教材：《信号与线性系统分析（第五版）》高等教育出版社，吴大正著

一、要点

（1）连续LTI系统的微分方程模型及其经典解，了解齐次解+特解的微分方程求解方法；
（2）系统响应的分解：掌握自由（固有）响应/强迫响应、瞬态响应/稳态响应、零输入响应/零状态响应的概念，能够熟练完成系统响应的分解；
（3，重点）0-和0+初始值问题，了解系统初始状态在0时刻产生突变的原因，熟练掌握0+初始值的求解方法；系统微分方程的算子表示法；
（4，重点）系统零输入响应和零状态响应的分别求解，熟练掌握求解方法。

二、问题与解答

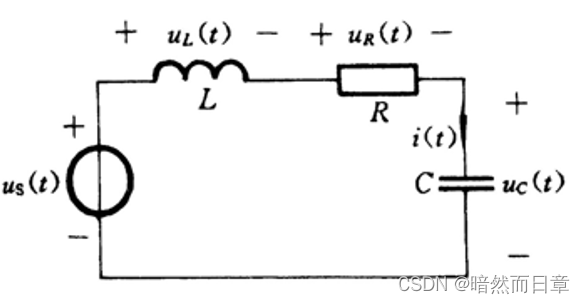
1、系统自由响应为什么又被称为固有响应，这种时域响应的模态（随时间的变化规律）主要取决于什么？它与系统外加的输入激励有没有关系？预备训练一的RLC电路，C1取两种不同值的情况下，所得到系统微分方程的特征根有什么不同（列出系统微分方程并求出其特征根）？这种不同对于系统的自由响应模态有何影响？二阶电路（如RLC电路）的过阻尼、欠阻尼、临界阻尼、无阻尼分别对应于特征根的何种情形？

2、试分析以下几个论断的正误：①零输入响应一定是自由响应；②自由响应一定是零输入响应；③零状态响应一定是强迫响应；④零状态响应包括自由响应和强迫响应。

3、为什么“微分方程等号右端含有冲激函数及其各阶导数时，响应y(t)及其各阶导数由0-到0+的瞬间将发生跃变”（教材p45），这反映了冲激或者冲激偶所具有的何种特性？

4、求解教材课后习题2.2（4），据此总结求0-到0+跃变的方法和步骤，特别注意与教材例2.1-3、2.1-4进行比较，说明如何确定等号右端冲激的阶次与等号左端y(t)的最高阶次的对应关系。

5、求解教材课后习题2.4（2），其中零状态响应分别用常规方法（教材例2.1-5方法）和微分特性（教材例2.1-6方法）这两种方法求解，并分别指出全响应中的自由响应/强迫响应、稳态响应/暂态响应。

6、动态系统的时域响应，可以理解为系统输出跟随输入指令，从一种状态到另一种状态的转换（例如数字电路中0、1电平的转换）。对于实际的物理系统来说，这种转换总是需要花费一定的时间的（转换不可能瞬时完成，需要一个过渡过程），而不能突变（思考：前面第3个讨论题所分析的0-到0+跃变，为什么在实际物理系统中不可能发生？）。针对预备训练一的RLC电路在方波输入激励下的响应（输出），从输出反应的速度、一个稳态到另一个稳态所用时间、输出过冲（超调）量大小等几个方面，比较分析电路工作于欠阻尼、过阻尼这两种状态，其过渡过程各自的特点。

1、系统的自由响应

系统自由响应为什么又被称为固有响应，这种时域响应的模态（随时间的变化规律）主要取决于什么？它与系统外加的输入激励有没有关系？（第1问）预备训练一的RLC电路，C1取两种不同值的情况下，所得到系统微分方程的特征根有什么不同（列出系统微分方程并求出其特征根）？这种不同对于系统的自由响应模态有何影响？（第2问）二阶电路（如RLC电路）的过阻尼、欠阻尼、临界阻尼、无阻尼分别对应于特征根的何种情形？（第3问）

（1）动态电路的完全响应中，已由初始条件确定待定系数k的微分方程通解部分，称为电路系统的自由响应。它的函数形式由电路系统本身结构决定，与外加激励无关，所以也称为固有响应。
（2）
在这里插入图片描述

在这里插入图片描述

（3）
在这里插入图片描述

2、各类响应的关系

试分析以下几个论断的正误：①零输入响应一定是自由响应；②自由响应一定是零输入响应；③零状态响应一定是强迫响应；④零状态响应包括自由响应和强迫响应。

（1）对
（2）错
（3）错
（4）对
(自由响应=固有响应）
在这里插入图片描述

3、冲激函数的特性

为什么“微分方程等号右端含有冲激函数及其各阶导数时，响应y(t)及其各阶导数由0-到0+的瞬间将发生跃变”（教材p45），这反映了冲激或者冲激偶所具有的何种特性？

0-是零输入时的初始状态，初始值是由系统的储能决定的；0+是加了输入后的初始状态，初始值受储能与激励的双重影响。
作用时间无穷小，反映了冲激或者冲激偶的瞬时特性。

4、初值求解问题

求解教材课后习题2.2（4），据此总结求0-到0+跃变的方法和步骤，特别注意与教材例2.1-3、2.1-4进行比较，说明如何确定等号右端冲激的阶次与等号左端y(t)的最高阶次的对应关系。

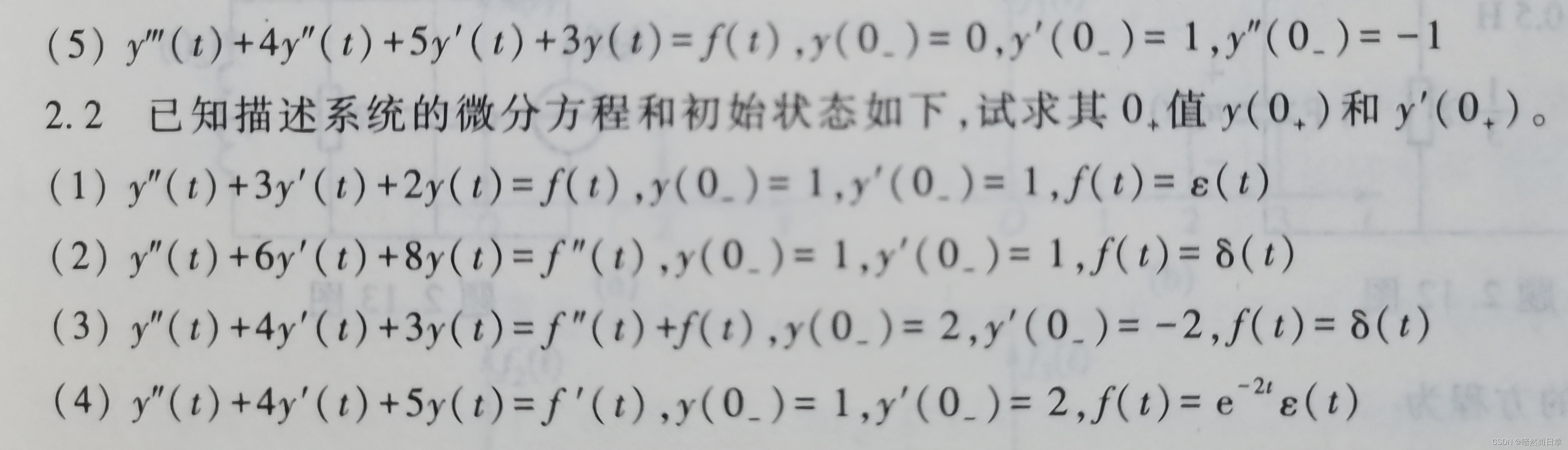
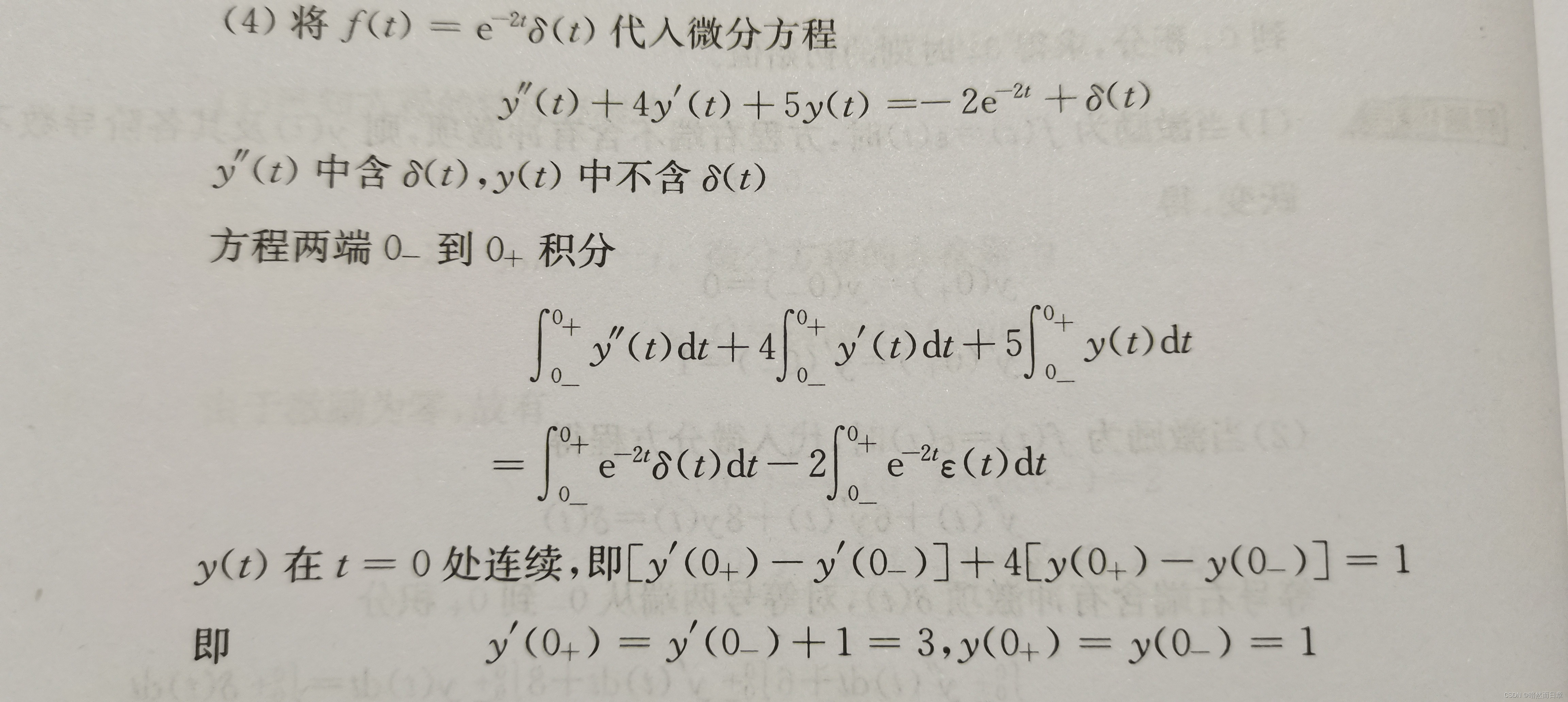
在这里插入图片描述

在这里插入图片描述
等号右端冲激函数的最高阶导数阶次与等号左端y(t)的最高导数阶次相等。
系统中从0-到0+有无跳变取决于微分方程右端是否包含冲激函数及其各阶导数，如果包含即发生了跳变，用冲激函数匹配法求出0+状态，冲激函数匹配法是根据t=0时刻微分方程左右两端的冲激函数及其各阶导数应该平衡等。
1、找最高阶，右端δ(t)最高阶对应左端最高阶。
2、由高到低列式子，直到出现阶跃信号u(t)。
3、把第二步列的式子带入到微分方程，系统进行匹配。
4、找出阶数对应的跳变值，r(k)(0+)=r(k)(0-)+跳变值。

5、零输入响应、零状态响应与全响应求解问题

求解教材课后习题2.4（2），其中零状态响应分别用常规方法（教材例2.1-5方法）和微分特性（教材例2.1-6方法）这两种方法求解，并分别指出全响应中的自由响应/强迫响应、稳态响应/暂态响应。

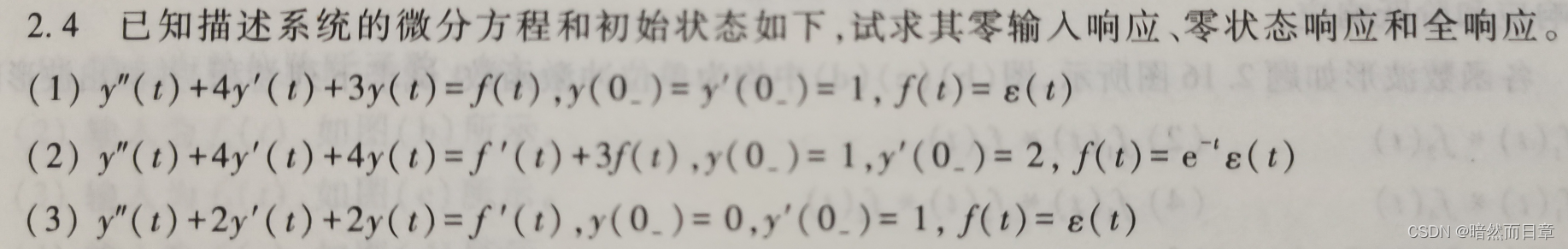
在这里插入图片描述
零状态响应用常规方法求解：

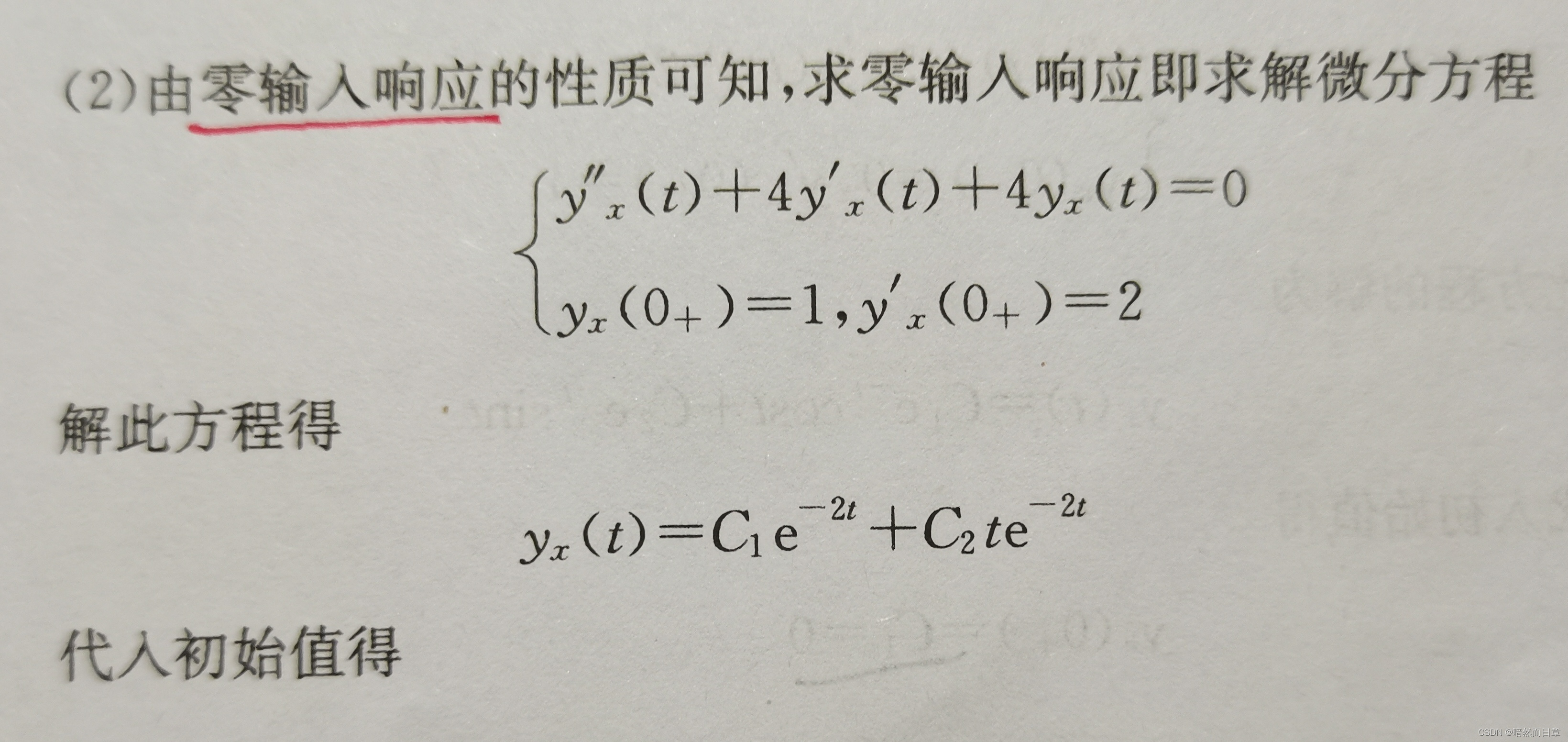
零状态响应部分用微分特性求解：

在这里插入图片描述

6、实际物理系统的响应过渡过程

动态系统的时域响应，可以理解为系统输出跟随输入指令，从一种状态到另一种状态的转换（例如数字电路中0、1电平的转换）。对于实际的物理系统来说，这种转换总是需要花费一定的时间的（转换不可能瞬时完成，需要一个过渡过程），而不能突变（思考：前面第3个讨论题所分析的0-到0+跃变，为什么在实际物理系统中不可能发生？（第一问））。针对预备训练一的RLC电路在方波输入激励下的响应（输出），从输出反应的速度、一个稳态到另一个稳态所用时间、输出过冲（超调）量大小等几个方面，比较分析电路工作于欠阻尼、过阻尼这两种状态，其过渡过程各自的特点。（第二问）
（1）从0-到0+是一种理想化的数学模型，现实中无法产生，因为需要满足冲激信号幅度无穷大，瞬时功率无穷大，变化速度无穷大。
（2）
一个系统受初扰动后不再受外界激励，因受到阻力造成能量损失而位移峰值渐减的振动称为阻尼振动。

欠阻尼：如果负载阻抗大于传输线的特性阻抗，那么负载端多余的能量就会反射回源端，由于负载端没有吸收全部能量，故称这种情况为欠阻尼。
输出反应的速度快、一个稳态到另一个稳态所用时间长、输出过冲（超调）量大。

过阻尼：如果负载阻抗小于传输线的特性阻抗，那么负载试图消耗比当前源端提供的能量更多的能量，故反射回来通知源端输送更多的能量，故称这种情况为过阻尼。
输出反应的速度慢、一个稳态到另一个稳态所用时间短、输出过冲（超调）量小。