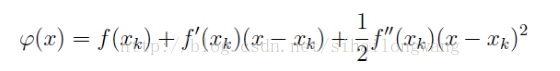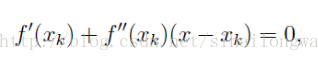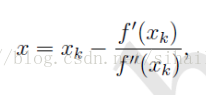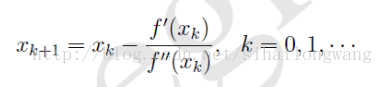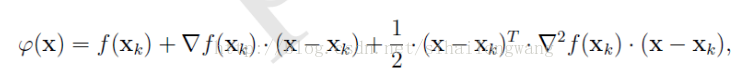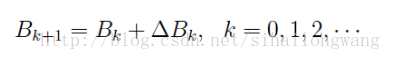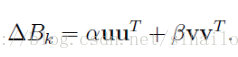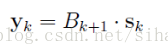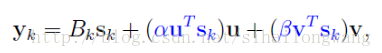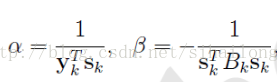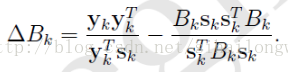实习点滴（8）--收敛优化方法：牛顿法、BFGS算法与L-BFGS算法

本文主要是介绍实习点滴（8）--收敛优化方法：牛顿法、BFGS算法与L-BFGS算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

        在了解CRF推导与参数估计的时候，会用到收敛优化方法去迭代求解凸优化问题，至此，总结一下我对牛顿法、BFGS算法和L-BFGS算法这三种方法的理解。

     牛顿法：

        方法思想：在现有极小点估计值附近对f(x)做二阶泰勒展开式，进而找到下一个极小点估计值。

        设：xk为当前极小点估计值， 我们要去求这个函数的最值，则二阶泰勒展开式为：

                                 

        若要求极值，则使其倒数等于0，然后得：

                                                             

        从而求得：

                                                                         

        若给定一个初始的x，可以得到一个迭代的格式：

                                                     

        我们扩展到N>1的情况，则得到：

           

        我们称一阶的矩阵为“梯度向量”或者“g矩阵”，二阶的矩阵为“海森矩阵”或者“H矩阵”。

        算法流程：

                           

        优缺点：

        【优点】：

          1、迭代一次就可以求解出最优解

          2、如果初始值选的合适的话，收敛速度快

        【缺点】：

          1、要求函数二阶可微

          2、收敛性和初始值选择依赖性大

          3、计算H矩阵计算量大

     BFGS算法：

        目前求解无约束非线性优化问题最常用的方法之一。

        方法思想：

        设：

                                                                        

        其中，B0一般取单位矩阵，通过迭代，将B接近于极值点。

        用待定系数法，设：

                                                                                             

        再加上以下条件：

                                                                                                            

        则有：

                                                                         

        

          可算出：

                                                                                       

        综上所述，得到：

                                                                                        

        算法流程：

                             

     L-BFGS算法：

        L-BFGS算法是对BFGS算法的一种改进。

        基本思想：不再存储完整的矩阵D，而是春初计算过程中的向量序列s,y；需要矩阵D的时候，利用向量序列s,y的计算来代替，而且，向量序列s,y也不是所有的都存，而是固定存最新的m个，每次计算D时，只利用最新的m个s和m个y

这篇关于实习点滴（8）--收敛优化方法：牛顿法、BFGS算法与L-BFGS算法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---