问题:江上有6个游艇站,游客可以从任意一个站租赁游艇,并在其下游任意一个站归还游艇,不同站之间的费用不同。
游艇出租站i到j之间的租金为r(i,j)。上下游情况以及各站点之间的费用如下:
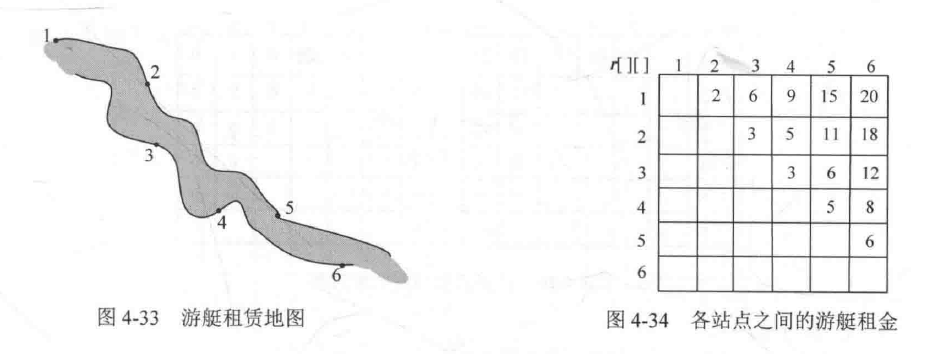
图片来源于陈小玉老师的《趣学算法》
思想:假设i到j经过在k停靠有最优情况,那么,原问题就分解为求解 i->k 子问题最优解与 k->j 子问题最优解的情况。
分析:
1.上述指出上游可以到下游中任意一个站规划游艇,那么,只能是序号低的站点到序号高的站点,所以,在租金矩阵中只会存在右三角的部分。
2.上述问题无外乎考虑的是直达还是经过中转然后到达目的站点。
注:我们需要进行以下推论,若存在1,2,3站点,1->3有两种情况,要么1->3,要么1->2->3,要是经过2站点中转,则1->3的花费最小,那么我们就知道了1->3的最佳策略是在2站点进行中转。
那么,继续,存在1,2,3,4站点,1->4的情况就更多了些,可以是1->4,也可以是1->2->4,或者是1->3->4,又或者是1->2->3->4这4中情况,有上述中的假设,1->3的最佳策略是在2站点进行中转,那么用于1->4策略中,1->2->3->4的情况一定优于1->3->4的情况。所以,这就引出了动态规划的核心要点,即原问题的最优解一定包含了子问题的最优解,即1->4(1->3->4)的最优解情况一定包含了1->3的最优解情况,那么,我们在开始要记录了子问题的最优解情况,后续则可以直接使用,
我们开始建立最优值的递归式:
已知我们的数据结构:m[i][j]的值表示两点之间的最短花费,s[i][j]的值表示两点之间的中转节点。
那么,若i==j,则m[i][j]==0;
若j==i+1,则m[i][j]==r[i][j],即m[i][j]表示两点间的直达代价,那么s[i][j]==0,因为s[i][j]表示两者间的中转点,而两点为直达,所以没有中转点;
若j>i+1,即两点间存在一个或者一个以上的中转点时,m[i][j]==min{m[i][k]+m[k][j],r[i][j]}
核心思想:假设i到j经过在k停靠有最优情况,那么,原问题就分解为求解 i->k 子问题最优解与 k->j 子问题最优解的情况,逐渐往下找出最小规模子问题的情况。
同时还需要注意一点就是,我们必须求出规模最小时的最优值,然后才能递推出规模较大时的最优值。而规模最小时为两个相邻点的情况,接着三个点,四个点......
但是我们知道i->k的代价,k->j的代价都是最小的(子问题最优用于母问题最优)
而事实上,i->k的最优情况在分析i->j之前我们已经得到,我们直接用就可以,没必要再重新分析。就是比如先以三个点为例,结果1->3的代价中,路径1->2->3的代价是低于路径1->3代价的,那么,我们就会在选择中记录要是有结果1->3的情况,我们就默认选择路径1->2->3。
同理在1->4的结果中,我们会尝试路径1->4,1->2->4,1->2->3->4而不会去尝试1->3->4。而在计算经过节点3进行中转的情况时,我们只需要关注的是3->4之间的代价,而结果1->3的代价已经由路径1->2->3求得。
所以,最后,若假设结果1->4的最佳路径是1->2->3->4,我们只需要知道4的前一节点是3,而不关心3的前一节点是谁,而到了3节点,我们才能发现其前一节点还需要经过2。
接下来进行代码分析:
初始化,我们让m[i][j]=r[i][j],s[i][j]=0,即将直达情况进行了第一遍记录,后续的比较就是逐次增加中转站点的个数,不断进行比较是经过中转后的代价最优还是直达最优,从而对代价表与中转表进行更新。

接下来,分析超过2个节点的情况,我们加入某个点作为两点间的中转点,看加入后代价是否优于之前,若代价优于直达,更新代价表,并将中转节点编号赋值给r[i][j]。
接下来上代码:
代码主要在函数printShortValue()较难理解,其实就是我们要从最小规模入手。
#include <iostream> using namespace std; const int N = 1024; int r[N][N],m[N][N],s[N][N]; int n; int b, t; void initArray() //初始化数组 {for(int i = 1; i <= n; i++){for(int j = i+1; j <= n; j++){m[i][j] = r[i][j];r[i][j] = 0;}} }void calShortValue() //计算数组中的最优代价情况 {for(int num = 3; num <= n; num++){ //num站点的长度,由小到大更新,则长度大的情况可以使用长度小的情况for(int i = 1; i <= n-num+1; i++){int j = i+num-1;for(int k = i+1; k < j; k++){if(m[i][k] + m[k][j] < m[i][j]){m[i][j] = m[i][k] + m[k][j];s[i][j] = k;}}}} }void printShortValue() //打印数组中最优代价情况 {for(int i = 1; i <= n; i++){for(int j = 1; j <= n; j++){if(j <= i){cout << " ";}else{cout << s[i][j];}cout << " ";}cout << "\n";} }void printShortPath(int b, int t) {if(s[b][t]==0){cout << "---" << t;return;}printShortPath(b,s[b][t]);printShortPath(s[b][t],t); }int main() {cout << "请输入站点个数:" << endl;cin >> n;cout << "请以此输入各站点间的代价:" << endl;for(int i = 1; i <= n; i++){for(int j = i+1; j <= n; j++){cin >> r[i][j];}}cout << "请输入源站点与目的站点:";cin >> b >> t;initArray();calShortValue();printShortValue();cout << "两点间的最小代价为:" << m[b][t] <<endl;cout << "两点间经过:" << b;printShortPath(b,t); }




