本文主要是介绍离散数学大作业:各城市通信总造价最小,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
- 问题描述
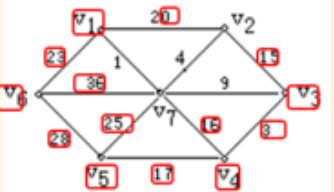
下图所示的赋权图表示某七个城市及预先算出它们之间的通信线路造价(单位:万元),试给出一个设计方案,使得各城市之间既能够通信又使总造价最小并计算其最小值.
编程求解以上问题(Kruskal算法或Prim算法)
- Prim基本原理
Prim算法从任意一个顶点开始,每次选择一个与当前顶点集最近的一个顶点,并将两顶点之间的边加入到树中。Prim算法在找当前最近顶点时使用到了贪婪算法。
算法描述:
1. 在一个加权连通图中,顶点集合V,边集合为E
2. 任意选出一个点作为初始顶点,标记为visit,计算所有与之相连接的点的距离,选择距离最短的,标记visit.
3. 重复以下操作,直到所有点都被标记为visit:
在剩下的点中,计算与已标记visit点距离最小的点,标记visit,证明加入了最小生成树。
流程图:

- 实验结果
- 程序输出结果
加入生成树集合的边:
v1——v7 权值:1
v7——v2 权值:4
v7——v3 权值:9
v3——v4 权值:3
v4——v5 权值:17
v1——v6 权值:23
总造价最小为57万元
- 通信线路图

- 实验代码
MAX = 9999
primgraph = [[MAX, 20, MAX, MAX, MAX, 23, 1],[ 20, MAX, 15, MAX, MAX, MAX, 4],[MAX, 15, MAX, 3, MAX, MAX, 9],[MAX, MAX, 3, MAX, 17, MAX, 16],[MAX, MAX, MAX, 17, MAX, 28, 25],[ 23, MAX, MAX, MAX, 28, MAX, 36],[ 1, 4, 9, 16, 25, 36, MAX]]
chararray = ['v1','v2','v3','v4','v5','v6','v7']
charlist = []
charlist.append(chararray[0])
mid = [] #mid[i]表示生成树集合中与点i最近的点的编号
lowcost = [] #lowcost[i]表示生成树集合中与点i最近的点构成的边最小权值 ,-1表示i已经在生成树集合中
lowcost.append(-1)
mid.append(0)
n = len(chararray)
for i in range(1,n): #初始化mid数组和lowcost数组lowcost.append(primgraph[0][i])mid.append(0)
sum = 0
for _ in range(1,n): #插入n-1个结点minid = 0min = MAXfor j in range(1,n): #寻找每次插入生成树的权值最小的结点if(lowcost[j]!=-1 and lowcost[j]<min):minid = jmin = lowcost[j]charlist.append(chararray[minid])print(chararray[mid[minid]]+'——'+chararray[minid]+'权值:'+str(lowcost[minid]))sum+=minlowcost[minid] = -1for j in range(1,n): #更新插入结点后lowcost数组和mid数组值if(lowcost[j]!=-1 and lowcost[j]>primgraph[minid][j]):lowcost[j] = primgraph[minid][j]mid[j] = minid
print("sum="+str(sum))
print("插入结点顺序:"+str(charlist))
这篇关于离散数学大作业:各城市通信总造价最小的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






