本文主要是介绍INS/GNSS组合导航(十)松耦合捷联车载定位解算示例,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.摘要
基于GNSS信号辅助IMU实现车载导航,可有效规避IMU积分误差累积效应及GNSS信号丢失导致位姿解算失准的问题,为此本文引入结合GNSS与IMU的松组合融合定位计算方法实现低成本车载IMU传感器的准确定位.
2.算法实现
2.1流程图
基于融合的INS/GNSS组合导航方法 实现位姿解算(求解PVA)的流程图如下。

2.2算法实现
2.2.1主要坐标系方向
对于车载导航算法解算过程,涉及的坐标系参见下图所示,均符合右手坐标系法则


2.2.2 IMU估算
定义时刻的导航状态量与IMU的观测量分别如下:
(1)
(2)
其中对应位置向量,
对应速度向量,
对应姿态向量(四元数表示法),
对应三个方向的加速度向量,
对应三个方向的角速度向量.
对于纯惯性导航系统INS的求解,将时间物理量离散化后,可采用下述非线性差分表达式进行递推得到.
(3)
其中,
(4)
(5)
(6)
(7)
其中对应的是IMU数据采样周期(s),
对应的是方向余弦矩阵DCM,即将body系(b-frame)中的向量旋转到navi系(n-frame).对于车载而言,通常因安装误差或人为调整,使得IMU传感器与车体之间存在一定安装倾角,则上述表达式对应的b-frame需对应调整为车体坐标系,而非通常意义的IMU坐标系(可将IMU的坐标系调整为车体的b系).
2.2.3 GNSS与IMU融合
上述章节给出了仅采用IMU实现解算的流程,通常单独的IMU解算只能维持较短时间,长时间则因积分累计误差,使得累计误差过大解算结果大幅偏移实际行驶轨迹.为此,采用结合GNSS的松组合解算方法,具体而言,借助卡尔曼滤波器(Kalman Filter)实现融合定位的位姿解算.
假定IMU的测量信号可采用下述表达式定义:
(8)
其中, 表示协方差矩阵
添加高斯白噪声后得到的测量噪声,
表示缓慢变化的测量偏差,可基于随机行走模拟其大小变化,即:
(9)
其中, 表示协方差矩阵
添加高斯白噪声后得到的随机行走噪声.
进一步结合上述表达式,给出真实的导航状态量与INS估测得到状态量
之间的误差
(10)
上式中,相应的得到位置误差为:, 速度误差为:
,姿态扰动量
可视作姿态量
变化到
所引起的欧拉角变化,实际是一个3x3的旋转矩阵.
结合相关文献,可得到 与
的关系式如下:
(11)
其中下标skew表示相应矩阵的反对称矩阵(skew symmetric,类似)
根据上述式(10)定义的误差向量,将测量信号 传递给INS求解表达式(3),对于较小的误差信号,可采用线性状态空间模型表述如下:
(12)
其中状态转移矩阵与噪声增益矩阵
分别定义如下:
(13)
(14)
(15)
(16)
进一步,对于GNSS信号接收器得到的位置测量值 可表述如下:
(17)
其中 是协方差矩阵添加高斯白噪声后得到GNSS测量噪声.
由此得到融合解算(KF解算所需)的误差输入量即为GNSS测量值与纯IMU估算量之差,即:
(18)
(19)
上述式(11)与式(19)所定义的状态空间模型即通常意义上的松组合条件下GNSS辅助的INS融合解算算法.
2.2.4 车体动力学模型
尽管借助GNSS可有效辅助IMU传感器对位置进行估计,然而在GPS信号丢失的情况下,位置误差迅速增加,使得导航解算显著偏离实际位置,估算失效.为此,可引入车体运动动力学模型.通常的做法是引入运动学约束.通常假定车辆无打滑现象,车体运动方向垂直方向都无速度分量,即与
均为0,仅考虑车体前进方向速度
。
(20)
(21)
对应的是方向余弦矩阵DCM,即将navi系(n-frame)旋转变换到车辆坐标系(p-frame)。实际行驶过程,上述两个方向的速度并非完全为0,为此适当松弛上述约束条件,即添加一个噪声项。
(22)
(23)
(24)
其中,
(25)
对于进一步可写成如下形式:
(26)
3.解算效果


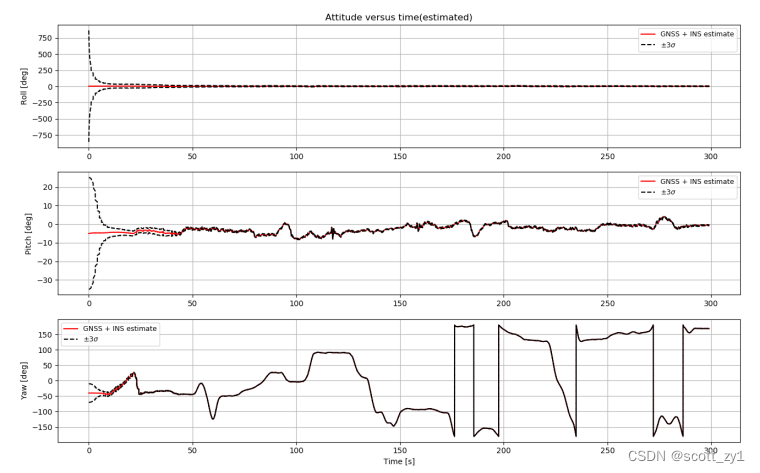
4.其它说明
本次松耦合解算只是一个简单的示例,对很多误差模型的处理进行了简化,实际车载定位解算需考虑更为全面的数学模型。
5.参考文献
1.Accuracy Improvement of Low Cost INS/GPS for Land Applications
2.GNSS-aided INS for land vehicle positioning and navigation
3.Tilt Sensing Using a Three-Axis Accelerometer
4.Design and Implementation Issues of a Portable Navigation System
5.Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems
这篇关于INS/GNSS组合导航(十)松耦合捷联车载定位解算示例的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



