拓端tecdat|R语言时间序列平稳性几种单位根检验（ADF，KPSS，PP）及比较分析

本文主要是介绍拓端tecdat|R语言时间序列平稳性几种单位根检验（ADF，KPSS，PP）及比较分析，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

最近我们被客户要求撰写关于单位根检验的研究报告，包括一些图形和统计输出。

时间序列模型根据研究对象是否随机分为确定性模型和随机性模型两大类。

随机时间序列模型即是指仅用它的过去值及随机扰动项所建立起来的模型,建立具体的模型,需解决如下三个问题模型的具体形式、时序变量的滞后期以及随机扰动项的结构。

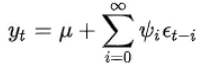
μ是yt的均值；ψ是系数，决定了时间序列的线性动态结构，也被称为权重，其中ψ0=1；{εt}为高斯白噪声序列，它表示时间序列{yt}在t时刻出现了新的信息，所以εt称为时刻t的innovation（新信息）或shock（扰动）。

单位根测试是平稳性检验的特殊方法。单位根检验是对时间序列建立ARMA模型、ARIMA模型、变量间的协整分析、因果关系检验等的基础。

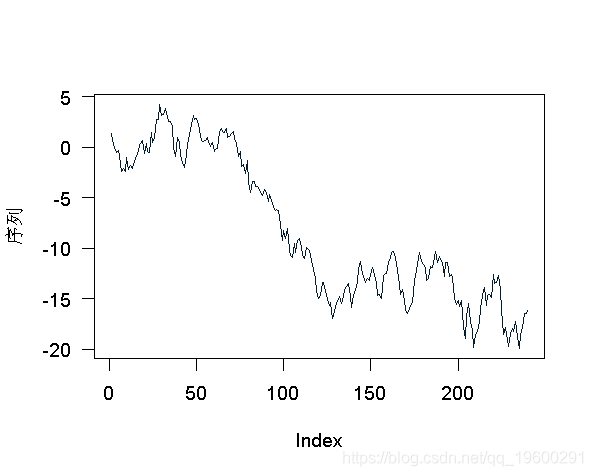
对于单位根测试，为了说明这些测试的实现，考虑以下系列


> plot(X,type="l")

Dickey Fuller（标准）

这里，对于Dickey-Fuller测试的简单版本，我们假设

$https://latex.csdn.net/eq?%20Y_t=\alpha+\beta%20t+\varphi%20Y_{t-1}+\varepsilon_t$

我们想测试是否（或不是）。我们可以将以前的表示写为

$https://latex.csdn.net/eq?%20\Delta%20Y_t=\alpha+\beta%20t+[\varphi-1]%20Y_{t-1}+\varepsilon_t$

所以我们只需测试线性回归中的回归系数是否为空。这可以通过学生t检验来完成。如果我们考虑前面的模型没有线性漂移，我们必须考虑下面的回归


Call:
lm(formula = z.diff ~ 0 + z.lag.1)Residuals:Min       1Q   Median       3Q      Max 
-2.84466 -0.55723 -0.00494  0.63816  2.54352 Coefficients:Estimate Std. Error t value Pr(>|t|)
z.lag.1 -0.005609   0.007319  -0.766    0.444Residual standard error: 0.963 on 238 degrees of freedom
Multiple R-squared:  0.002461,	Adjusted R-squared:  -0.00173 
F-statistic: 0.5873 on 1 and 238 DF,  p-value: 0.4442

我们的测试程序将基于学生t检验的值，

> summary(lm(z.diff~0+z.lag.1 ))$coefficients[1,3]
[1] -0.7663308

这正是计算使用的值

ur.df(X,type="none",lags=0)############################################################### 
# Augmented Dickey-Fuller Test Unit Root / Cointegration Test # 
############################################################### The value of the test statistic is: -0.7663

可以使用临界值（99%、95%、90%）来解释该值

> qnorm(c(.01,.05,.1)/2)
[1] -2.575829 -1.959964 -1.644854

如果统计量超过这些值，那么序列就不是平稳的，因为我们不能拒绝这样的假设。所以我们可以得出结论，有一个单位根。实际上，这些临界值是通过


############################################### 
# Augmented Dickey-Fuller Test Unit Root Test # 
############################################### Test regression none Call:
lm(formula = z.diff ~ z.lag.1 - 1)Residuals:Min       1Q   Median       3Q      Max 
-2.84466 -0.55723 -0.00494  0.63816  2.54352 Coefficients:Estimate Std. Error t value Pr(>|t|)
z.lag.1 -0.005609   0.007319  -0.766    0.444Residual standard error: 0.963 on 238 degrees of freedom
Multiple R-squared:  0.002461,	Adjusted R-squared:  -0.00173 
F-statistic: 0.5873 on 1 and 238 DF,  p-value: 0.4442Value of test-statistic is: -0.7663 Critical values for test statistics: 1pct  5pct 10pct
tau1 -2.58 -1.95 -1.62

R有几个包可以用于单位根测试。

Augmented Dickey-Fuller Testdata:  X
Dickey-Fuller = -2.0433, Lag order = 0, p-value = 0.5576
alternative hypothesis: stationary

这里还有一个检验零假设是存在单位根。但是p值是完全不同的。

p.value
[1] 0.4423705
testreg$coefficients[4]
[1] 0.4442389

增广Dickey-Fuller检验

回归中可能有一些滞后现象。例如，我们可以考虑

$https://latex.csdn.net/eq?%20\Delta%20Y_t=\alpha+\beta%20t+[\varphi-1]%20Y_{t-1}+\psi%20\Delta%20Y_{t-1}+\varepsilon_t$

同样，我们需要检查一个系数是否为零。这可以用学生t检验来做。


> summary(lm(z.diff~0+z.lag.1+z.diff.lag ))Call:
lm(formula = z.diff ~ 0 + z.lag.1 + z.diff.lag)Residuals:Min       1Q   Median       3Q      Max 
-2.87492 -0.53977 -0.00688  0.64481  2.47556 Coefficients:Estimate Std. Error t value Pr(>|t|)
z.lag.1    -0.005394   0.007361  -0.733    0.464
z.diff.lag -0.028972   0.065113  -0.445    0.657Residual standard error: 0.9666 on 236 degrees of freedom
Multiple R-squared:  0.003292,	Adjusted R-squared:  -0.005155 
F-statistic: 0.3898 on 2 and 236 DF,  p-value: 0.6777coefficients[1,3]
[1] -0.7328138

该值是使用

> df=ur.df(X,type="none",lags=1)############################################### 
# Augmented Dickey-Fuller Test Unit Root Test # 
############################################### Test regression none Call:
lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)Residuals:Min       1Q   Median       3Q      Max 
-2.87492 -0.53977 -0.00688  0.64481  2.47556 Coefficients:Estimate Std. Error t value Pr(>|t|)
z.lag.1    -0.005394   0.007361  -0.733    0.464
z.diff.lag -0.028972   0.065113  -0.445    0.657Residual standard error: 0.9666 on 236 degrees of freedom
Multiple R-squared:  0.003292,	Adjusted R-squared:  -0.005155 
F-statistic: 0.3898 on 2 and 236 DF,  p-value: 0.6777Value of test-statistic is: -0.7328 Critical values for test statistics: 1pct  5pct 10pct
tau1 -2.58 -1.95 -1.62

同样，也可以使用其他包：

Augmented Dickey-Fuller Testdata:  X
Dickey-Fuller = -1.9828, Lag order = 1, p-value = 0.5831
alternative hypothesis: stationary

结论是一样的（我们应该拒绝序列是平稳的假设）。

带趋势和漂移的增广Dickey-Fuller检验

到目前为止，我们的模型中还没有包括漂移。但很简单（这将被称为前一过程的扩充版本）：我们只需要在回归中包含一个常数，

> summary(lm)Residuals:Min       1Q   Median       3Q      Max 
-2.91930 -0.56731 -0.00548  0.62932  2.45178 Coefficients:Estimate Std. Error t value Pr(>|t|)  
(Intercept)  0.29175    0.13153   2.218   0.0275 *
z.lag.1     -0.03559    0.01545  -2.304   0.0221 *
z.diff.lag  -0.01976    0.06471  -0.305   0.7603  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 0.9586 on 235 degrees of freedom
Multiple R-squared:  0.02313,	Adjusted R-squared:  0.01482 
F-statistic: 2.782 on 2 and 235 DF,  p-value: 0.06393

考虑到方差输出的一些分析，这里获得了感兴趣的统计数据，其中该模型与没有集成部分的模型进行了比较，以及漂移，

> summary(lmcoefficients[2,3]
[1] -2.303948
> anova(lm$F[2]
[1] 2.732912

这两个值也是通过

ur.df(X,type="drift",lags=1)############################################### 
# Augmented Dickey-Fuller Test Unit Root Test # 
############################################### Test regression drift Residuals:Min       1Q   Median       3Q      Max 
-2.91930 -0.56731 -0.00548  0.62932  2.45178 Coefficients:Estimate Std. Error t value Pr(>|t|)  
(Intercept)  0.29175    0.13153   2.218   0.0275 *
z.lag.1     -0.03559    0.01545  -2.304   0.0221 *
z.diff.lag  -0.01976    0.06471  -0.305   0.7603  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 0.9586 on 235 degrees of freedom
Multiple R-squared:  0.02313,	Adjusted R-squared:  0.01482 
F-statistic: 2.782 on 2 and 235 DF,  p-value: 0.06393Value of test-statistic is: -2.3039 2.7329 Critical values for test statistics: 1pct  5pct 10pct
tau2 -3.46 -2.88 -2.57
phi1  6.52  4.63  3.81

我们还可以包括一个线性趋势，

> temps=(lags+1):n
lm(z.diff~1+temps+z.lag.1+z.diff.lag )Residuals:Min       1Q   Median       3Q      Max 
-2.87727 -0.58802 -0.00175  0.60359  2.47789 Coefficients:Estimate Std. Error t value Pr(>|t|)  
(Intercept)  0.3227245  0.1502083   2.149   0.0327 *
temps       -0.0004194  0.0009767  -0.429   0.6680  
z.lag.1     -0.0329780  0.0166319  -1.983   0.0486 *
z.diff.lag  -0.0230547  0.0652767  -0.353   0.7243  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 0.9603 on 234 degrees of freedom
Multiple R-squared:  0.0239,	Adjusted R-squared:  0.01139 
F-statistic:  1.91 on 3 and 234 DF,  p-value: 0.1287> summary(lmcoefficients[3,3]
[1] -1.98282
> anova(lm$F[2]
[1] 2.737086

而R函数返回

ur.df(X,type="trend",lags=1)############################################### 
# Augmented Dickey-Fuller Test Unit Root Test # 
############################################### Test regression trend Residuals:Min       1Q   Median       3Q      Max 
-2.87727 -0.58802 -0.00175  0.60359  2.47789 Coefficients:Estimate Std. Error t value Pr(>|t|)  
(Intercept)  0.3227245  0.1502083   2.149   0.0327 *
z.lag.1     -0.0329780  0.0166319  -1.983   0.0486 *
tt          -0.0004194  0.0009767  -0.429   0.6680  
z.diff.lag  -0.0230547  0.0652767  -0.353   0.7243  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 0.9603 on 234 degrees of freedom
Multiple R-squared:  0.0239,	Adjusted R-squared:  0.01139 
F-statistic:  1.91 on 3 and 234 DF,  p-value: 0.1287Value of test-statistic is: -1.9828 1.8771 2.7371 Critical values for test statistics: 1pct  5pct 10pct
tau3 -3.99 -3.43 -3.13
phi2  6.22  4.75  4.07
phi3  8.43  6.49  5.47

KPSS 检验

在这里，在KPSS过程中，可以考虑两种模型：漂移模型或线性趋势模型。在这里，零假设是序列是平稳的。
代码是

ur.kpss(X,type="mu")####################### 
# KPSS Unit Root Test # 
####################### Test is of type: mu with 4 lags. Value of test-statistic is: 0.972 Critical value for a significance level of: 10pct  5pct 2.5pct  1pct
critical values 0.347 0.463  0.574 0.73

在这种情况下，有一种趋势

ur.kpss(X,type="tau")####################### 
# KPSS Unit Root Test # 
####################### Test is of type: tau with 4 lags. Value of test-statistic is: 0.5057 Critical value for a significance level of: 10pct  5pct 2.5pct  1pct
critical values 0.119 0.146  0.176 0.216

再一次，可以使用另一个包来获得相同的检验（但同样，不同的输出）

KPSS Test for Level Stationaritydata:  X
KPSS Level = 1.1997, Truncation lag parameter = 3, p-value = 0.01> kpss.test(X,"Trend")KPSS Test for Trend Stationaritydata:  X
KPSS Trend = 0.6234, Truncation lag parameter = 3, p-value = 0.01

至少有一致性，因为我们一直拒绝假设。

Philipps-Perron 检验

Philipps-Perron检验基于ADF过程。代码

> PP.test(X)Phillips-Perron Unit Root Testdata:  X
Dickey-Fuller = -2.0116, Truncation lag parameter = 4, p-value = 0.571

另一种可能的替代方案是

> pp.test(X)Phillips-Perron Unit Root Testdata:  X
Dickey-Fuller Z(alpha) = -7.7345, Truncation lag parameter = 4, p-value
= 0.6757
alternative hypothesis: stationary

比较

我不会花更多的时间比较不同的代码，在R中，运行这些测试。我们再花点时间快速比较一下这三种方法。让我们生成一些或多或少具有自相关的自回归过程，以及一些随机游走，让我们看看这些检验是如何执行的：


> for(i in 1:(length(AR)+1)
+ for(s in 1:1000){
+ if(i!=1) X=arima.sim
+ M2[s,i]=(pp.testp.value)
+ M1[s,i]=(kpss.testp.value)
+ M3[s,i]=(adf.testp.value)
+ }

这里，我们要计算检验的p值超过5%的次数，


> plot(AR,P[1,],type="l",col="red",ylim=c(0,1)
> lines(AR,P[2,],type="l",col="blue")
> lines(AR,P[3,],type="l",col="green")

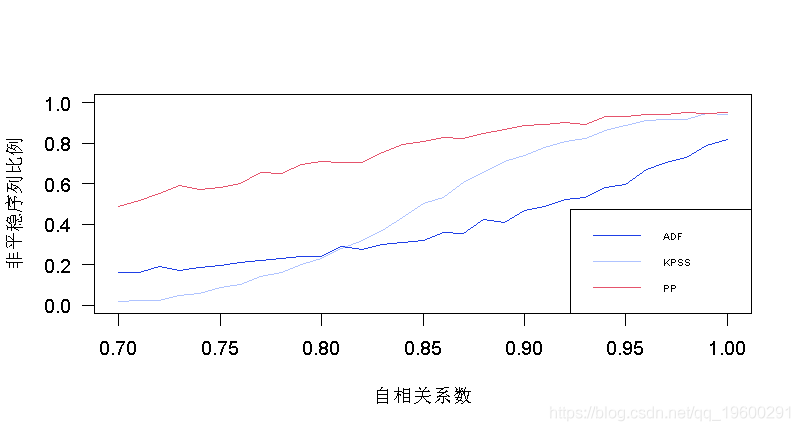
我们可以在这里看到Dickey-Fuller测试的表现有多不稳定，因为我们的自回归过程中有50%(至少)被认为是非平稳的。

这篇关于拓端tecdat|R语言时间序列平稳性几种单位根检验（ADF，KPSS，PP）及比较分析的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

拓端tecdat|R语言时间序列平稳性几种单位根检验（ADF，KPSS，PP）及比较分析

最近我们被客户要求撰写关于单位根检验的研究报告，包括一些图形和统计输出。

相关文章

python panda库从基础到高级操作分析

C语言中%zu的用法解读

MySQL中EXISTS与IN用法使用与对比分析

MySQL 内存使用率常用分析语句

深度解析Nginx日志分析与499状态码问题解决

Linux系统中查询JDK安装目录的几种常用方法

Java获取当前时间String类型和Date类型方式

C语言进阶(预处理命令详解)

Python实现批量提取BLF文件时间戳

Go语言并发之通知退出机制的实现