本文主要是介绍图的应用:校园导游系统(含Dijkstra和Floyd算法),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
/*
问题描述:用无向网表示你所在学校的校园景点平面图,图中顶点表示主要景点,
存放景点的编号、名称、简介等信息,图中的边表示景点间的道路,存放路径长度等信息。
要求能够回答有关景点介绍、游览路径等问题。
基本要求:查询各景点的相关信息;
查询图中任意两个景点间的最短路径;
查询图中任意两个景点间的所有路径;增加、删除、更新有关景点和道路的信息。
选作内容:
1.求多个景点的最佳(最短)游览路径。
2.区分机动车道和人行道。
3.实现导游图的仿真界面。 注:很惭愧,有关基于邻接矩阵存储的无向图某两点之间的所有路径的相关算法我真的不会,另外由于时间关系选做的我也没做,对不起王阿川老师T_T
*/ #include <iostream>
#include <stdio.h>
#include <string.h>
#include <iomanip>
#include <stdlib.h>
#include <math.h>
#define INFINITY 65535 //无穷大,即不相邻
#define MAX_VERTEX_NUM 20 //最大的顶点个数
using namespace std;
typedef int VRType;
typedef char InfoType; typedef struct{ int num; char name[20]; char introduce[100];
}VertexType; typedef struct ArcCell{ VRType adj; //距离 InfoType *info;//边的信息
}ArcCell,AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; typedef struct { VertexType vex[MAX_VERTEX_NUM];//顶点向量 AdjMatrix arcs; //邻接矩阵 int vexnum,arcnum; //顶点数和边数
}MGraph; void create(MGraph &g,VertexType site[])
{ int i,j; g.vexnum=11; g.arcnum=12; for(i=0;i<11;i++) g.vex[i]=site[i]; for(i=0;i<g.vexnum;i++) for(j=0;j<g.vexnum;j++) g.arcs[i][j]={INFINITY,NULL}; g.arcs[0][1].adj=200; g.arcs[1][2].adj=150; g.arcs[2][3].adj=50; g.arcs[3][4].adj=100; g.arcs[4][5].adj=50; g.arcs[5][9].adj=300; g.arcs[6][7].adj=450; g.arcs[6][9].adj=500; g.arcs[0][4].adj=300; g.arcs[0][7].adj=250; g.arcs[9][10].adj=700; g.arcs[7][8].adj=20; for(i=0;i<g.vexnum;i++) for(j=0;j<g.vexnum;j++) g.arcs[j][i].adj= g.arcs[i][j].adj; } void output(MGraph g,int i)//根据序号i输出对应的景点的相关信息
{ printf("景点序号:%d\n",i); printf("景点名称:%s\n",g.vex[i-1].name); printf("景点简介:%s\n",g.vex[i-1].introduce);
} void search(MGraph g)
{ int i; printf("请输入你想查找的景点的序号:\n"); scanf("%d",&i); output(g,i);
} void Shortest_Path_Dijkstra(MGraph g,int v0,int P[][20],int D[20])
{ int v,w,i,j,final[20],min; for(v=0;v<g.vexnum;v++){ final[v]=0; D[v]=g.arcs[v0][v].adj; for(w=0;w<g.vexnum;w++) P[v][w]=-1; if(D[v]<INFINITY) { P[v][0]=v0; P[v][1]=v; } } D[v0]=0; final[v0]=1; for(i=1;i<g.vexnum;i++){ min=INFINITY; for(w=0;w<g.vexnum;w++) if(!final[w]&&D[w]<min) { v=w; min=D[w]; } final[v]=1; for(w=0;w<g.vexnum;w++) if(!final[w]&&(min+g.arcs[v][w].adj<D[w])){ D[w]=min+g.arcs[v][w].adj; for(j=0;j<g.vexnum;j++) { P[w][j]=P[v][j]; if(P[w][j]==-1)//在p[w][]第一个等于-1的地方加上顶点w { P[w][j]=w; break; } } } }
} void ShortestPath_FLOYD(MGraph g, int P[20][20][20], int D[][20])
{ int u,v,w,i,j; for(v=0;v<g.vexnum;v++) for(w=0;w<g.vexnum;w++) { D[v][w]=g.arcs[v][w].adj; for(u=0; u<g.vexnum;u++) P[v][w][u]=-1; if(D[v][w]<INFINITY) { P[v][w][0]=v; P[v][w][1]=w; } } for(u=0;u<g.vexnum;u++) for(v=0;v<g.vexnum;v++) for(w=0;w<g.vexnum;w++) if(D[v][u]<INFINITY&&D[u][w]<INFINITY&&D[v][u]+D[u][w]<D[v][w]) { //更新D D[v][w]=D[v][u]+D[u][w]; //更新p,从v到w的路径是从v到u,再从u到w的所有路径 for(i=0;i<g.vexnum;i++) { if(P[v][u][i]!=-1) P[v][w][i]=P[v][u][i]; else break; } for(j=1;j<g.vexnum;j++)//注意:这里j从1开始而不是从0开始,因为从v到u的路径最后一个顶点是u, 而从u到w的路径第一个顶点是u,只需打印u一次即可。 { if(P[u][w][j]!=-1) P[v][w][i++]=P[u][w][j]; else break; } } } void update(MGraph &g)
{ int i; printf("请输入你想查找的景点的序号:\n"); scanf("%d",&i); if(i>=1&&i<=11) { printf("请输入新的景点名称:\n"); scanf("%s",g.vex[i-1].name); printf("请输入新的景点名称简介:\n"); scanf("%s",g.vex[i-1].introduce); }
} void add_arc(MGraph &g)
{ int v1,v2,n; printf("请输入你想增加的边两端的顶点序号:\n"); printf("请输入第一个顶点号:\n"); scanf("%d",&v1); printf("请输入第二个顶点号:\n"); scanf("%d",&v2); if(g.arcs[v1-1][v2-1].adj==INFINITY) { printf("请输入两点之间的距离:\n"); scanf("%d",&g.arcs[v1-1][v2-1].adj); g.arcs[v2-1][v1-1].adj=g.arcs[v1-1][v2-1].adj; printf("增加成功!\n"); } else {
LL0: printf("这两点已经有路径存在了,你想要修改它吗?想的话请按1,不想请按2:\n"); scanf("%d",&n); if(n==1) { printf("请输入两点之间的新的距离:\n"); scanf("%d",&g.arcs[v1-1][v2-1].adj); g.arcs[v2-1][v1-1].adj=g.arcs[v1-1][v2-1].adj; printf("修改成功!\n"); } else if(n==2) { printf("增加失败,呜呜呜T_T\n"); } else { printf("你的输入有误,请重新输入!\n"); goto LL0; } }
} void delete_arc(MGraph &g)
{ int v1,v2; printf("请输入你想删除的边两端的顶点序号:\n"); printf("请输入第一个顶点号:\n"); scanf("%d",&v1); printf("请输入第二个顶点号:\n"); scanf("%d",&v2); if(g.arcs[v1-1][v2-1].adj!=INFINITY) { g.arcs[v1-1][v2-1].adj=g.arcs[v2-1][v1-1].adj=INFINITY; printf("删除成功!\n"); } else { printf("删除失败!这两个点之间本来就没有直接通路,你还删它干嘛???\n"); }
} void display_num(MGraph g)
{ int i; printf("景点序号 景点名称\n"); for(i=0;i<g.vexnum;i++) { if(i+1<10) printf("%d %s\n",g.vex[i].num,g.vex[i].name); else printf("%d %s\n",g.vex[i].num,g.vex[i].name); }
} void display_all(MGraph g)
{ int i; printf("景点序号 景点名称 景点简介\n"); for(i=0;i<g.vexnum;i++) { if(i+1<10) printf("%d %s %s\n",g.vex[i].num,g.vex[i].name,g.vex[i].introduce); else printf("%d %s %s\n",g.vex[i].num,g.vex[i].name,g.vex[i].introduce); }
} void menu()
{ printf("\n1.显示所有景点的序号\n"); printf("2.查询所有景点的信息\n"); printf("3.查询某个景点的信息\n"); printf("4.查询某个景点到其他景点的最短路径\n"); printf("5.输出任意两个景点之间的最短路径\n"); printf("6.增加某一条边\n"); printf("7.删除某一条边\n"); printf("8.修改某一条边\n"); printf("9.退出系统\n");
} int main()
{ int v1,v2,P1[20][20],P2[20][20][20],D1[20],D2[20][20],i,j,k; MGraph g; VertexType site[11]={ {1,"主楼","林学院和土木学院的老巢"}, {2,"理学楼","理学院老师和学生办公和上课的地方"}, {3,"动资楼","动资院的老巢"}, {4,"锦绣楼","马克思和外院最喜欢上课的地方"}, {5,"丹青楼","我现在就在丹青9楼苦逼的敲代码"}, {6,"行政楼","李大大办公的地方"}, {7,"操场","情侣们秀恩爱的最佳去处"}, {8,"9A学生公寓","信息学院男生的窝"}, {9,"老食堂","味道比新食堂好那么一点点"}, {10,"体育馆","大一上乒乓球的时候去过,听说郭德纲也去踩了踩"}, {11,"新食堂","难吃"} }; create(g,site); printf("欢迎来到校园导游系统!\n");
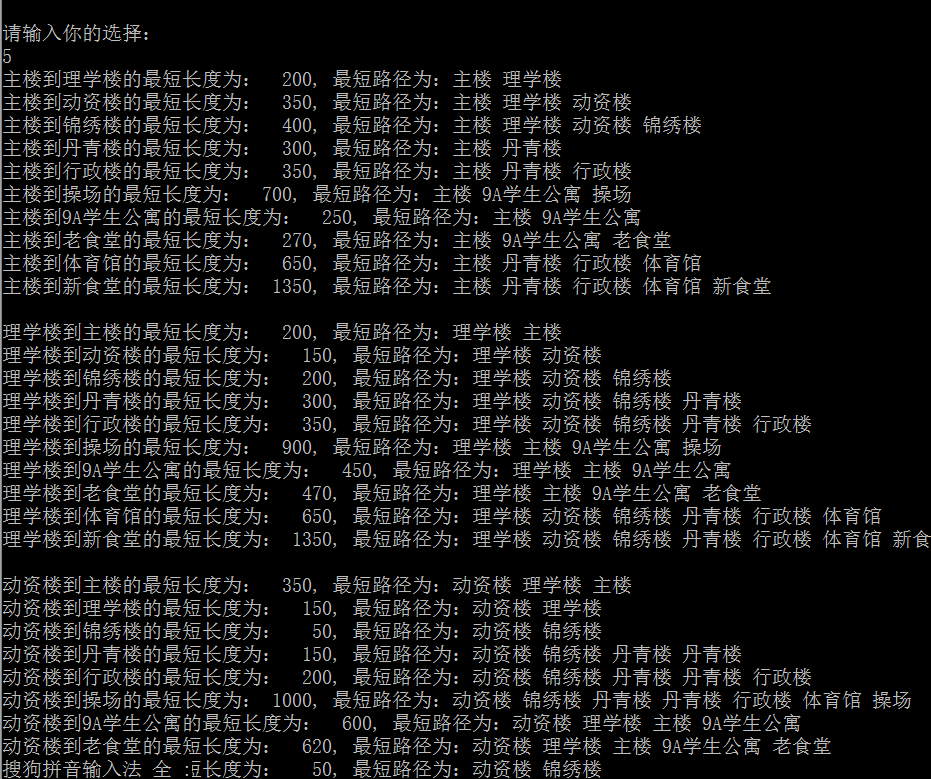
LL1:menu(); printf("\n请输入你的选择:\n"); scanf("%d",&i); switch(i) { case 1: display_num(g); goto LL1; break; case 2: display_all(g); goto LL1; break; case 3: search(g); goto LL1; break; case 4: printf("请输入景点的序号:\n"); scanf("%d",&k); Shortest_Path_Dijkstra(g,k-1,P1,D1); for(i=1;i<g.vexnum;i++){ printf("%d号(%s)到%d号(%s):",k,g.vex[k-1].name,i+1,g.vex[i].name); for(j=0;P1[i][j]!=-1;j++) printf("%d号(%s) ",P1[i][j]+1,g.vex[P1[i][j]].name); printf("\n距离为:%d\n",D1[i]); puts(""); } goto LL1; break; case 5: ShortestPath_FLOYD(g,P2,D2); for(i=0; i<g.vexnum; i++) { for(int j=0; j<g.vexnum; j++) { if(i!=j) { if(D2[i][j]!=INFINITY) { cout<<g.vex[i].name<<"到"<<g.vex[j].name<<"的最短长度为:"<<setw(5)<<D2[i][j]<<", 最短路径为:"; for(int k=0; k<g.vexnum; k++) { if(P2[i][j][k]!=-1) cout<<g.vex[P2[i][j][k]].name<<" "; else break; } puts(""); } else cout<<g.vex[i].name<<"到"<<g.vex[j].name<<"不可达"<<endl; } } puts(""); } goto LL1; break; case 6: add_arc(g); goto LL1; break; case 7: delete_arc(g); goto LL1; break; case 8: update(g); goto LL1; break; case 9: printf("谢谢你的使用,寨见!\n"); exit(0); goto LL1; break; default: printf("你的输入有误,请重新输入!\n"); goto LL1; break; }
} 这篇关于图的应用:校园导游系统(含Dijkstra和Floyd算法)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!