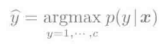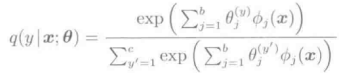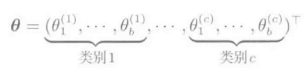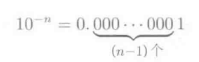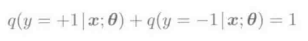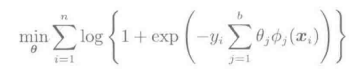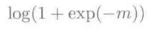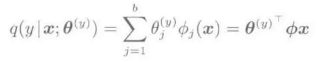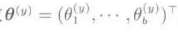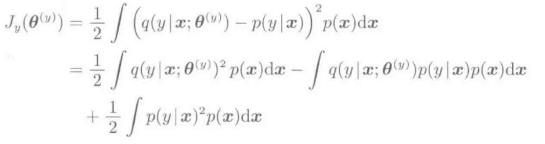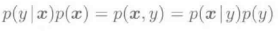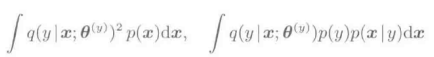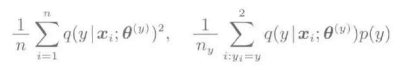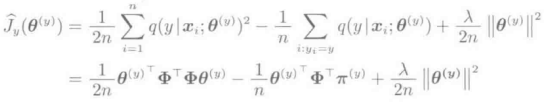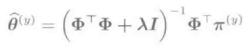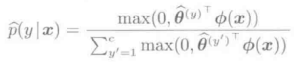本文主要是介绍有监督分类：概率分类法（Logistic），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
1.前言
前面我介绍的都是确定模式所属类别的模式识别算法。对于模式基于概率进行分类的手法称为概率分类法。这是这一篇博客重点讨论的内容。基于概率的模式识别，是指与模式x所对应的类别y的后验概率p(y|x)进行学习。其所属类别为后延概率达到最大值时所对应的类别。
类别的后验概率p(y=y'|x).可以理解为模式x属于类别y的可信度。通过这样的方法，在可信度非常低的时候就不用强行进行分类，从而避免了错误分类，而且可以设置一些实用的选项，比如吧这样的样本丢掉。另外，基于概率的模式识别还有一个优势，就是对于多种类别分类问题通常会有较好的分类结果。
2.Logistic回归
先谈一谈简单又实用的Logistic回归。2.1 Logistic模型的最大似然估计
Logistic回归，使用线性对数函数对分类后验概率p(y|x)进行模型化。
上式中，分母是与所有的y=1,...,c对应的，满足概率总和为1的约束条件的正则化项。上述的模型q(y|x:Θ)中包含的参数{Θj}j=1->b，在每个类别y=1,...,c中都不一样，因此包含所有参数的向量Θ有bc次维。
Logistic回归模型的学习，通过对数似然为最大师的最大似然估计进行求解。似然函数是指，将手头的训练样本{（xi,yi）}i=1->n由现在的模型生成的概率，看作是关于参数Θ的函数，对数似然是指其对数：
似然是q(yi|xi,Θ)经过n次相乘的结果，例如对于所有的i=1,...,n，q(yi|xi,Θ)=0.1的时候，其似然：
是一个非常小的值，经常会发生丢为的现象。对于这种情况，一般使用对数来解决，即利用将乘法变换为加法的方法来防止丢位现象的发生。Logistic回归学习模型有下事的最优化问题来定义：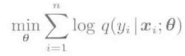
上面的目标函数对于参数Θ是可以微分的，因此我们还可以用梯度下降策略来求最大似然估计的解Θ’。概率梯度下降法的Logistic回归学习算法如下图所示：
2.2 对数高斯模型
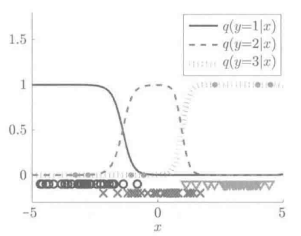
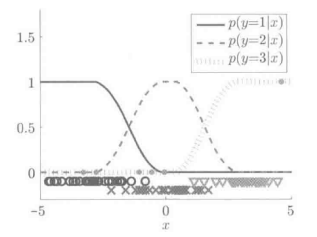
下图表示的是对对数高斯核模型进行Logistic回归学习的实例。
在该例中，高斯核的带宽h=1。
通过结果，我们可以看出，类别的后验概率P(y|x)得到了很好的学习。2.3 使用Logistic损失最小化学习来解释
首先从2分类问题y∈{+1,-1}进行说明：
通过使用上述关系式，Logistic模型的参数个数就可以由2b个降为b个。
这个模型的对数似然最大化的准则：
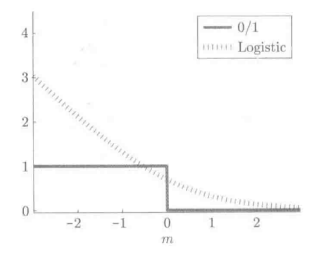
可以改写为上述形式。根据关于参数的线性模型：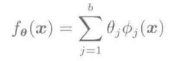
的间隔m=fΘ(x)y，可以知道上式与使用Logistic损失：
的Logistic损失最小化学习是等价的。如下图所示：
Logistic损失函数
3.最小二乘概率分类
这里只是简单性回顾一下在平方误差准则下进行与Logistic回归相同学习的最小二乘概率分类器。最小二乘概率分类器，对于各个类别y=1,...,c的后验概率p(y|x)，使用于参数相关的线性模型：
进行模型化。与Logistic模型不同的是，这个模型仅仅依赖与各个类别y对应的参数
然后，对这个模型进行学习，是下面的平方误差最小：
上式中，P(x)表示的是训练输入样本的概率密度函数。上式的第二项可以进行变形为：
上式中，p(x|y)是属于类别y的训练输入样本的概率密度函数，p(y)表示的是训练输出样本{yi}i=1->n的概率密度函数。我们应该注意到，Jy中包含了如下比较难以处理的：
分别表示与p(x)和P(x|y)相关的数学期望值。这些期望值一般无法直接计算，而是采用样本的平均值进行模拟：
应该注意的是，对于Jy，他的第三项与Θ无关，所以没必要再研究。此外，我们引入L2正则化项，得到如下的计算准则：
可以发现，这个学习准则是关于Θ的凸二次式，对其进行偏微分并置零可以得到最优解。
然而，如果按照上式计算，类别的后验概率可能会出现负的。因此，需要对负的输出加一个下届为零的约束条件：
下面是最小二乘概率分类的例子，使用的数据与Logistic回归数据一致，分类结果如下图所示：
最小二乘概率分类的实例
4.总结
最小二乘概率分类器能够得到与Logistic回归基本相同的学习结果。Logistic回归模型包括正则项，因此，与各个类别的基函数个数b和类别c相对应，其参数个数为bc个。另一方面，最小二乘概率分类器使用了没有正则化的线性模型，所以是对有b个参数的模型，对各类别进行c次独立学习的过程。在类别数c很大的情况下，最小二乘概率分类效率更高一点。同时，由于Logistic回归学习包含非线性的对数函数，必须要通过反复迭代的方式进行求解，需要花费大量的学习时间。但是，最小而成概率分类器中可以得到解析解，更有效率。但是，最小二乘概率分类器也不是完美无瑕的。因为，最小二乘概率分类器的输出为概率的形式，所以需要进行一系列的后期处理。在样本容量很大的情况下，后续处理几乎没影响，范式当训练样本非常小的情况下，就会导致学习效率低下。因此，一般的处理方式是，当训练样本是较多的时候，采用最小二乘分类器；而当训练样本较少的时候，则采用Logistic回归方法。
这篇关于有监督分类：概率分类法（Logistic）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
