（六）Tiki-taka算法（TTA）求解无人机三维路径规划研究（MATLAB）

本文主要是介绍（六）Tiki-taka算法（TTA）求解无人机三维路径规划研究（MATLAB），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、无人机模型简介：

单个无人机三维路径规划问题及其建模_IT猿手的博客-CSDN博客

参考文献：

[1]胡观凯,钟建华,李永正,黎万洪.基于IPSO-GA算法的无人机三维路径规划[J].现代电子技术,2023,46(07):115-120

二、Tiki-taka算法（TTA）简介

极致攻守算法（Tiki-Taka Algorithm，TTA）由Mohd Fadzil Faisae Ab. Rashid于2020年提出，该算法受tiki-taka 足球风格的短传、球员定位和保持控球的特点所启发。其旨在控制控球权并利用其战术优势击败对手，TTA算法新颖高效。单目标应用：Tiki-taka算法（TTA）求解太阳能光伏模型MATLAB_IT猿手的博客-CSDN博客

参考文献：

[1]Ab. Rashid, M.F.F. (2021), "Tiki-taka algorithm: a novel metaheuristic inspired by football playing style", Engineering Computations, Vol. 38 No. 1, pp. 313-343. Tiki-taka algorithm: a novel metaheuristic inspired by football playing style | Emerald Insight

[2]Zamli, Kamal Z , Kader, et al. Selective chaotic maps Tiki-Taka algorithm for the S-box generation and optimization.

三、TTA求解无人机路径规划

（1）部分代码

close all
clear  
clc
addpath('./Algorithm/')%添加算法路径
warning off;
%% 三维路径规划模型定义
global startPos goalPos N
N=2;%待优化点的个数(可以修改)
startPos = [10, 10, 80]; %起点(可以修改)
goalPos = [80, 90, 150]; %终点(可以修改)
SearchAgents_no=30; % 种群大小(可以修改)
Function_name='F2'; %F1:随机产生地图 F2：导入固定地图
Max_iteration=50; %最大迭代次数(可以修改)
% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
[Best_score,Best_pos,curve]=TTA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);%算法优化求解
AlgorithmName='TTA';%算法名字
figure
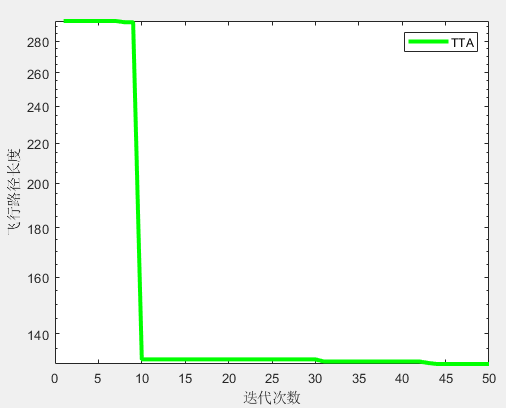
semilogy(curve,'Color','g','linewidth',3)
xlabel('迭代次数');
ylabel('飞行路径长度');
legend(AlgorithmName)
display(['算法得到的最优适应度: ', num2str(Best_score)]); 
Position=[Best_pos(1:dim/3); Best_pos(1+dim/3:2*(dim/3)); Best_pos(1+(2*dim/3):end)]'; %优化点的XYZ坐标（每一行是一个点）
plotFigure(Best_pos,AlgorithmName)%画最优路径

（2）部分结果

无人机飞行路径坐标：

   1.0000000e+01   1.0000000e+01   8.0000000e+019.8730326e+00   1.0493499e+01   8.0724276e+019.8013981e+00   1.1013766e+01   8.1472324e+019.7839525e+00   1.1560279e+01   8.2243381e+019.8195523e+00   1.2132512e+01   8.3036681e+019.9070534e+00   1.2729942e+01   8.3851461e+011.0045312e+01   1.3352043e+01   8.4686955e+011.0233185e+01   1.3998292e+01   8.5542399e+011.0469528e+01   1.4668164e+01   8.6417028e+011.0753197e+01   1.5361136e+01   8.7310079e+011.1083048e+01   1.6076682e+01   8.8220786e+011.1457938e+01   1.6814278e+01   8.9148384e+011.1876724e+01   1.7573400e+01   9.0092109e+011.2338260e+01   1.8353524e+01   9.1051197e+011.2841403e+01   1.9154126e+01   9.2024883e+011.3385010e+01   1.9974680e+01   9.3012403e+011.3967937e+01   2.0814664e+01   9.4012991e+011.4589040e+01   2.1673551e+01   9.5025883e+011.5247175e+01   2.2550819e+01   9.6050315e+011.5941198e+01   2.3445943e+01   9.7085522e+011.6669965e+01   2.4358399e+01   9.8130740e+011.7432334e+01   2.5287661e+01   9.9185203e+011.8227159e+01   2.6233207e+01   1.0024815e+021.9053298e+01   2.7194511e+01   1.0131881e+021.9909606e+01   2.8171049e+01   1.0239642e+022.0794939e+01   2.9162297e+01   1.0348022e+022.1708155e+01   3.0167731e+01   1.0456945e+022.2648108e+01   3.1186826e+01   1.0566333e+022.3613656e+01   3.2219058e+01   1.0676111e+022.4603654e+01   3.3263903e+01   1.0786201e+022.5616958e+01   3.4320837e+01   1.0896529e+022.6652426e+01   3.5389334e+01   1.1007016e+022.7708912e+01   3.6468871e+01   1.1117586e+022.8785274e+01   3.7558924e+01   1.1228164e+022.9880367e+01   3.8658968e+01   1.1338672e+023.0993048e+01   3.9768478e+01   1.1449035e+023.2122173e+01   4.0886931e+01   1.1559175e+023.3266597e+01   4.2013802e+01   1.1669017e+023.4425178e+01   4.3148567e+01   1.1778483e+023.5596772e+01   4.4290702e+01   1.1887498e+023.6780234e+01   4.5439682e+01   1.1995984e+023.7974421e+01   4.6594983e+01   1.2103867e+023.9178189e+01   4.7756080e+01   1.2211068e+024.0390395e+01   4.8922450e+01   1.2317511e+024.1609894e+01   5.0093568e+01   1.2423121e+024.2835542e+01   5.1268909e+01   1.2527820e+024.4066197e+01   5.2447950e+01   1.2631532e+024.5300714e+01   5.3630166e+01   1.2734181e+024.6537949e+01   5.4815032e+01   1.2835691e+024.7776759e+01   5.6002025e+01   1.2935984e+024.9015999e+01   5.7190620e+01   1.3034984e+025.0254526e+01   5.8380293e+01   1.3132615e+025.1491197e+01   5.9570519e+01   1.3228801e+025.2724867e+01   6.0760775e+01   1.3323464e+025.3954392e+01   6.1950535e+01   1.3416530e+025.5178630e+01   6.3139276e+01   1.3507920e+025.6396435e+01   6.4326473e+01   1.3597558e+025.7606664e+01   6.5511602e+01   1.3685369e+025.8808174e+01   6.6694139e+01   1.3771275e+025.9999821e+01   6.7873559e+01   1.3855201e+026.1180460e+01   6.9049337e+01   1.3937069e+026.2348949e+01   7.0220951e+01   1.4016804e+026.3504142e+01   7.1387875e+01   1.4094329e+026.4644897e+01   7.2549584e+01   1.4169566e+026.5770070e+01   7.3705556e+01   1.4242441e+026.6878517e+01   7.4855265e+01   1.4312876e+026.7969093e+01   7.5998187e+01   1.4380796e+026.9040656e+01   7.7133798e+01   1.4446122e+027.0092062e+01   7.8261573e+01   1.4508780e+027.1122166e+01   7.9380988e+01   1.4568692e+027.2129825e+01   8.0491519e+01   1.4625783e+027.3113895e+01   8.1592642e+01   1.4679975e+027.4073232e+01   8.2683832e+01   1.4731193e+027.5006693e+01   8.3764565e+01   1.4779359e+027.5913134e+01   8.4834316e+01   1.4824398e+027.6791410e+01   8.5892562e+01   1.4866232e+027.7640379e+01   8.6938777e+01   1.4904786e+027.8458896e+01   8.7972438e+01   1.4939983e+027.9245818e+01   8.8993021e+01   1.4971747e+028.0000000e+01   9.0000000e+01   1.5000000e+02