1-n范围内的质数查找：埃拉托斯特尼筛法

质数查找思路

质数定义

质数是一个自然数，且除了1和它本身以外没有其他因数。换句话说，如果一个数大于1，且只有两个正因数（1和它本身），那么它就是一个质数。例如，2、3、5、7、11、13等都是质数。注意，1和0不是质数。

根据质数的定义，质数p的倍数必然有其他因数（至少包括p本身），所以它们不可能是质数。因此，我们在使用埃拉托斯特尼筛法求质数时，对于每一个已知的质数p，都需要将所有p的倍数标记为非质数。

例如，当p=2时，我们将所有2的倍数（即所有偶数）标记为非质数。然后，找到下一个还未被标记为非质数的数（即3），将所有3的倍数标记为非质数，以此类推。这样，剩下的未被标记的数就都是质数了。

在1–9范围内排查质数，遍历2和3的情况如图所示。

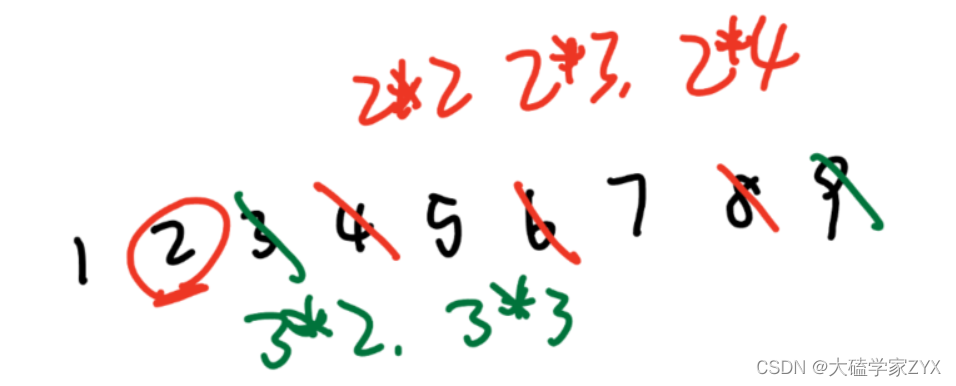
代码思路

代码方面的思路：

我们先定义一个is_prime数组 这个数组初始化为大小是n，初值全部是1。

i从2到n开始遍历（因为0和1不是质数）。遇到不是质数的，就让对应的下标i的数值变成0，最后，得到的所有值是1的下标i就是n以内所有的质数。

埃氏筛法是使用两层循环来判断0–N范围内的质数，第一层循环遍历小于等于n的所有数字，第二层循环对遍历到的数字，去除<=n范围内他们的所有倍数。

写法

在1–n范围内，用埃拉托斯特尼筛法找出所有的质数的写法：

// 先设定一个数组，大小为n,初值全部为1
// 从2开始，对于每一个i，如果i是质数，那么i的所有倍数都不是质数
// 只需要检查到 sqrt(n) ，因为如果 n 不是质数，那么它必定有一个小于等于 sqrt(n) 的因子
for (int i = 2; i * i <= n; ++i) {if (is_prime[i]==1) {for (int j = i * 2; j <= n; j += i) {is_prime[j] = 0;}}
}

重要逻辑：第一层for循环结束条件是i * i <= n而不是i<=n

理论上来说，我们确实应该在第一层循环遍历所有数字。

但是，有一个基于数论的重要性质：如果一个数n不是质数，那么它必然可以被某个小于等于sqrt(n)的数整除。

（某数字被x整除，就是指当前数字/x没有余数）

例如，8不是一个质数，我们可以看到2和4是8的因数，2*4等于8，所以8可以被2和4整除。在这个例子中，sqrt(8)大约等于2.83，所以2是小于等于sqrt(8)的数，它可以整除8。实际上，对于任何非质数，我们总是可以找到至少一个小于等于它的平方根的因数。

设想一下，如果一个数n不是质数，那么它至少有一对因数。设这对因数为a和b（a ≤ b）。如果a和b都大于sqrt(n)，那么a * b将大于n，这与假设a和b是n的因数矛盾；同样，如果a和b都小于等于sqrt(n)，那么a * b将小于n，也与假设矛盾。因此，对于n的任何一对因数，必然有一个小于等于sqrt(n)，另一个大于等于sqrt(n)。

因此，在埃拉托斯特尼筛法中，我们只需要检查到sqrt(n)就可以了。

我们只需要将从2到sqrt(n)的所有数的倍数剔除，就能得到所有的质数。这样也可以大大降低筛选质数的时间复杂度，使其在处理大规模数据时更高效。\

第二层循环如何筛查i所有倍数

筛所有倍数的逻辑：设定一个数字j，从j=i*2开始，每次循环j+=i，就是增加了一倍。

for(int j=i*2;j<=n;j+=i)

通过这个逻辑寻找所有小于或等于n的i的倍数，然后将它们标记为非质数。

完整版：返回0-n正整数中所有质数

#include <vector>
#include <cmath>
using namespace std;//返回0--n正整数中所有的质数
vector<int>judgePrime(int n){//包括0，所以要定义n+1vector<int>isPrime = (n+1,1);vector<int>result;//0和1不是质数isPrime[0]=isPrime[1]=0;//搜索i到sqrt(n)for(int i=2;i*i<=n;i++){if(isPrime[i]==1){for(int j=i*2;j<=n;j+=i){isPrime[j]=0;}}}//result就是isPrime数组中所有值为1的下标for(int i=2;i<=n;i++){if(isPrime[i]==1){result.push_back(i);}}return result;}

时间复杂度

埃拉托斯特尼筛法的时间复杂度是O(n log log n)。

这是因为在计算质数的时候，我们首先从2开始，然后找出2的所有倍数并将它们标记为非质数。然后，我们找到下一个仍然被标记为质数的数（在这个例子中是3），并找出3的所有倍数并将它们标记为非质数。我们继续这个过程，直到我们已经检查了所有小于等于sqrt(n)的数。由于每个数只被标记一次，所以总的操作次数是n/2+n/3+n/5+…，这个级数的和近似为n log log n。

例题

leetcode 6916.和等于目标的质数对2761. 和等于目标值的质数对 - 力扣（LeetCode）

给你一个整数 n 。如果两个整数 x 和 y 满足下述条件，则认为二者形成一个质数对：

• 1 <= x <= y <= n
• x + y == n
• x 和 y 都是质数

请你以二维有序列表的形式返回符合题目要求的所有 [xi, yi] ，列表需要按 xi 的 非递减顺序 排序。如果不存在符合要求的质数对，则返回一个空数组。

**注意：**质数是大于 1 的自然数，并且只有两个因子，即它本身和 1 。

示例 1：

输入：n = 10
输出：[[3,7],[5,5]]
解释：在这个例子中，存在满足条件的两个质数对。 
这两个质数对分别是 [3,7] 和 [5,5]，按照题面描述中的方式排序后返回。

示例 2：

输入：n = 2
输出：[]
解释：可以证明不存在和为 2 的质数对，所以返回一个空数组。 

提示：

• 1 <= n <= 10^6

解法：

class Solution {
public:vector<vector<int>> findPrimePairs(int n) {vector<vector<int>>result;vector<int>isPrime(n+1,1);isPrime[0]=0;isPrime[1]=0;//先调整i的数组，让数组里所有非质数下标对应的数值为0for(int i=2;i*i<=n;i++){if(isPrime[i]==1){for(int j=i*2;j<=n;j+=i){isPrime[j]=0;}}}//在n以内找质数对for(int i=2;i<=n/2;i++){if(isPrime[i]==1&&isPrime[n-i]==1){//当我们试图创建一个一维向量加入二维数组，必须要用{}而不是[]result.push_back({i,n-i});//把质数对加入结果}}return result;}
};

参考资料：

算法数学知识总结