蓝桥杯python组--基础训练---2、#一个数如果恰好等于它的因子之和，这个数就称为“完数”，；例如：6=1+2+3,找出1000以内的

题目

找出n以内的完数，如1000以内。
完全数（Perfect number），又称完美数或完备数，是一些特殊的自然数。它所有的真因子（即除了自身以外的约数）的和（即因子函数），恰好等于它本身。
例如：6=1+2+3；28=1+2+4+7+14；…

思路1

# 循环输出1到1000之间的数  range():含头不含尾
for i in range(1,1001):# 此时i代表1-1000之间所有的数# 定义和的初始值sum = 0# 构造数字的因子for j in range(1,i):#     因子:能被i整除的是i的因子if i % j == 0:#     只要是i的因子那么就相加sum += j# 如果 因子相加的和  等于i本身那么这个数就是完数if sum == i:print(f"{i}是完数")

或者也可以这样写

for i in range(1,1000):s = []for j in range(1,i):if i%j == 0:s.append(j)if sum(s) == i:print(i)

结果

思路2

from functools import reduce
def sum(a,b):return a+b
for i in range(2,1001):l = [1]for j in range(2,int(i/2+1)):if i%j==0:l.append(j)if i == reduce(sum,l):print(i)print(l)

结果

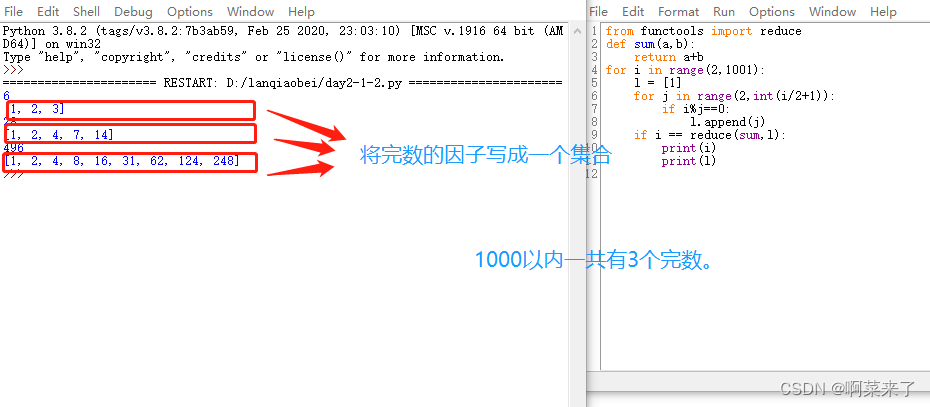
思路3

count = 0
for i in range(1,1001):list1 = []for j in range(1,i):if i%j==0:list1.append(j)if sum(list1)==i:#sum函数求和count +=1print('%d是完数,因子是'%i,list1)
print('1000以内的完数总共有%d个'%count)

结果

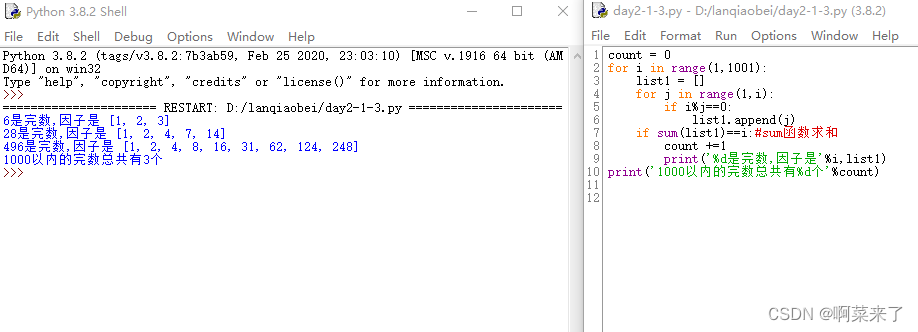
思路4

count  = 0
for i in range(2,1000):s = 0for j in range(1, i):if(i%j==0):s=s+jif(s==i):count = count + 1print(i)
print("1~1000的完全数共有{}个".format(count))

结果

思路5

a = []                                     # 创建空列表用于储存因子for i in range(2, 1000):              # 取除数for j in range(1, i):                  # 取小于除数的数作为被除数if i % j == 0:                # 如果两数相除，取余为0，也就是能整除，说明是因子a.append(j)                    # 将因子储存在列表里if sum(a) == i:                   # 当除数为i的情况完成后，将列表中的数求和，看是否满足因子相加等于除数的条件print(f"{i}是完数，因子包括{a}")    # 若符合，则输出完数和因子a.clear()                         # 将列表元素清除，进行下一个（i+1）的情况

结果

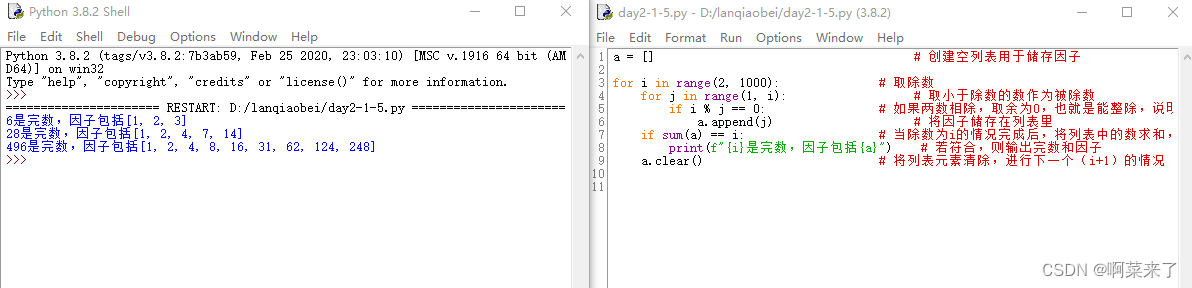
思路6

这个方法也是可以的，但是他不能在idle上运行。比赛的时候不能用pycharm。

结果

思路7

判断这个数是否是完数。但是并不能找出n以内的完数，也不能写出他们的因子。

n = int(input('::'))
c1 = 0
i = 1 
while i<=n-1: # 注意:要小于nif n%i == 0:c1+=ii+=1
if c1==n:print('这个数是完数')
else:print('这个数不是完数')

结果

思路8

def n(n):count = 0for i in range(1,n):if n%i==0:count +=iif count==n:return Trueelse:return Falsefor i in range(1,1001):# 1-1000判断if n(i):print(i)

结果

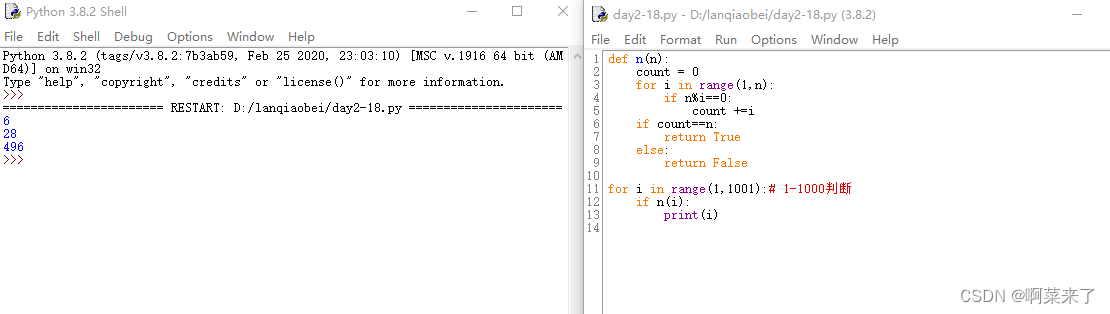
思路9

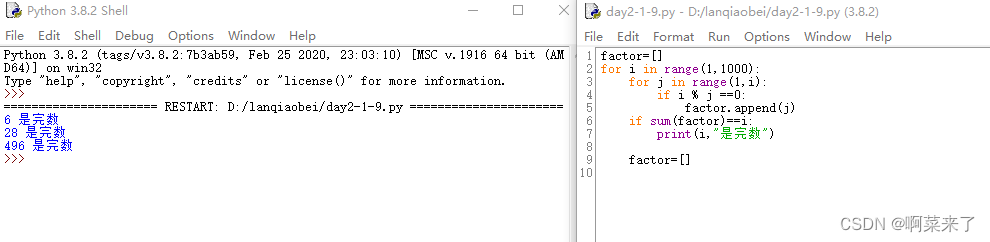
factor=[] 
for i in range(1,1000):for j in range(1,i):if i % j ==0:factor.append(j)if sum(factor)==i:print(i,"是完数")factor=[]

结果

总结

感觉这些方法都是大同小异，选择一个比较合适的就可以了。
列举这几种方法是方便大家学习。有不同的方法可以在评论留言。