本文主要是介绍Matlab通信仿真系列——信号的傅里叶(Fourier)分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
微信公众号上线,搜索公众号小灰灰的FPGA,关注可获取相关源码,定期更新有关FPGA的项目以及开源项目源码,包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等

本节目录
一、连续信号傅里叶变换
1、定义
2、fourier和ifourier函数
3、傅里叶级数
4、X(kΩ0)和X(jΩ)
二、离散信号的傅里叶变换
1、定义
2、Matlab频谱图绘制
3、Matlab验证DTFT的频移
4、Matlab验证的DTFT卷积性质
5.Matlab验证DFT的卷积性质
三、Matlab源码
1、fourier和ifourier函数源码
2、Matlab频谱图绘制源码
3、Matlab验证DTFT的频移源码
4、Matlab验证的DTFT卷积性质源码
5、Matlab实现DFT和IDFT运算
6、Matlab验证DFT的卷积性质源码
本节内容
信号的傅里叶Fourier分析包括了连续信号傅里叶变换、离散信号的傅里叶变换。
一、连续信号傅里叶变换
1、定义
设x(t)为连续时间信号,如果x(t)绝对可积,即
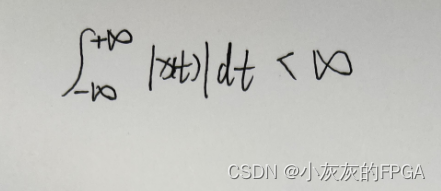
则x(t)的傅里叶变换存在,并定义为
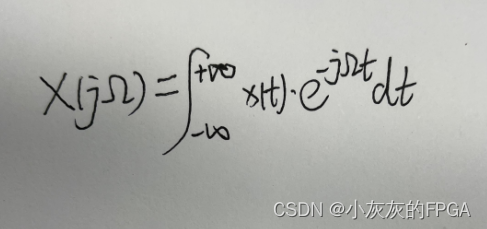
其反变换为
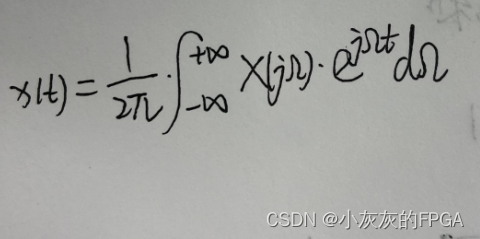
上述式中Ω=2πf,单位为rad/s
X(JΩ)=|X(JΩ)|e^(Jφ(Ω)),其中|X(JΩ)|表示幅频特性,φ(Ω)表示相频特性。
2、fourier和ifourier函数
Matlab中提供了求解傅里叶变换及其逆变换的函数
F=fourier(f)表示函数f的傅里叶变换,返回的是关于ω的函数。
f=ifourier(F)表示函数F的逆变换,默认的独立变量是ω,返回的是关于x的函数。
在使用fourier和ifourier函数之前,必须用syms命令对所用的变量进行符合说明。同时返回得到的函数仍是符合变量,因此应用ezplot绘图。

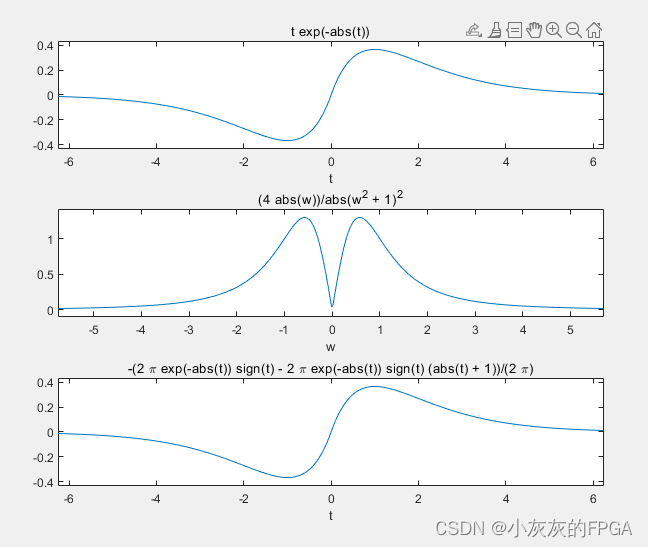
3、傅里叶级数
只有非周期信号才有傅里叶变换。
若x(t)满足狄利克雷条件,可以将其展开为傅里叶级数,
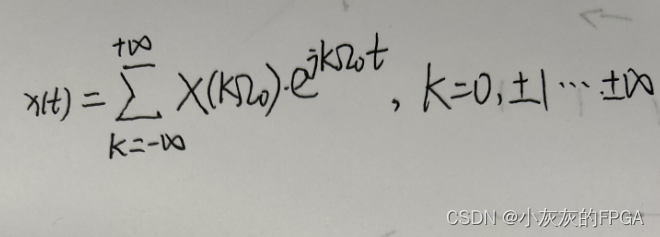
式中Ω0=2πf0,表示信号x(t)的基波频率;kΩ0为第k次谐波频率;
X(kΩ0)表示x(t)在k次谐波处的傅里叶级数,幅度表示信号x(t)所包含的频率为kΩ0的成分大小。
周期信号x(t)可以由无数的复正弦{e^(jkΩ0t),k=0,±1,…,±∞}作为基本信号再乘以不同的加权值X(kΩ0)复合而成。X(kΩ0)是频率kΩ0相应复正弦的幅度。
X(kΩ0)仅在k=0,±1,…,±∞取值,故在频率轴上为离散值,

X(kΩ0)用复数表示为
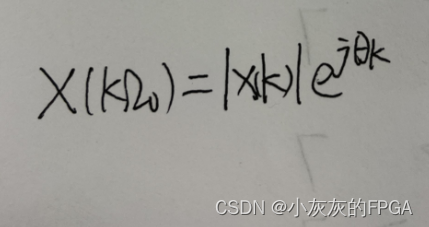
|X(k)|表示频率为nf0的分量的振幅;θk表示频率为nf0的分量的相位。
4、X(kΩ0)和X(jΩ)
X(kΩ0)是Ω轴上的离散函数,取Ω的整数倍;X(jΩ)是Ω的连续函数。
X(kΩ0)是谐波振幅的表述;X(jΩ)是频谱密度的表述。
二、离散信号的傅里叶变换
1、定义
离散信号h(n)为线性时不变系统的单位抽样响应,且绝对可和的,即满足
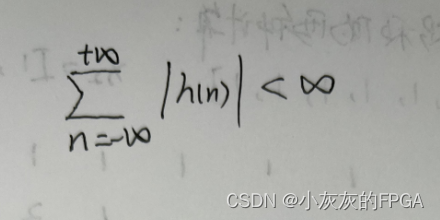
系统的频率响应,即离散时间序列的傅里叶变换DTFT为:
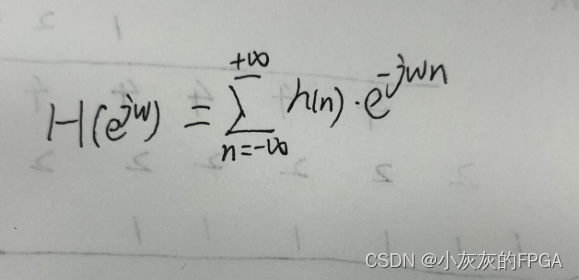
傅里叶逆变换IDTFT为:
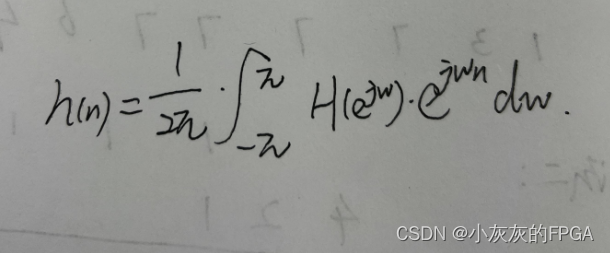
其中H(e^(jω))是ω的周期为2π的连续周期函数,ω表示弧度,数字频率。

2、Matlab频谱图绘制
matlab代码示例:
①求序列h1(n)=e^(-|0.1n|)的离散傅里叶变换,
其中-15≤n≤15
②求序列h2(n)=1的离散傅里叶变换,
其中0≤n≤20
傅里叶变换参考上述的公式进行算,
需要留意“n1'”表示n1的转置。

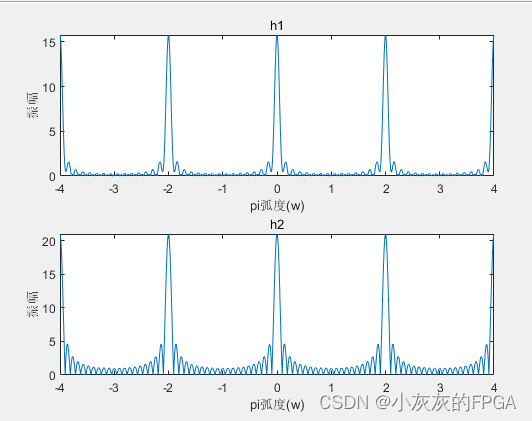
3、Matlab验证DTFT的频移
离散时间信号的DTFT的频移性质,序列乘以复指数序列对应于频域的频移。
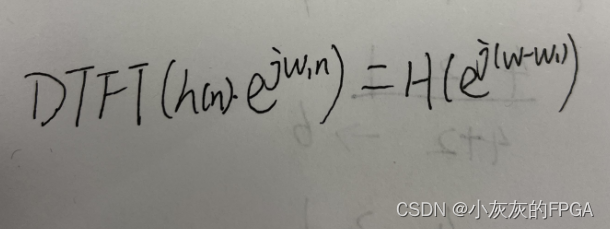
matlab代码示例:
①求序列h(n)=1的DTFT,其中0≤n≤20
②求序列x(n)=h(n)e^(jπn/4)
③求序列y(n)=h(n)e^(jπn/2)
x(n)是序列h(n)平移了π/4
y(n)是序列h(n)平移了π/2
4、Matlab验证的DTFT卷积性质
一个单位脉冲响应为h(n)的系统对输入序列x(n)的输出为y(n)=x(n)*h(n)
根据DTFT卷积性质可得:
Y(e^(jw))=DTFT[y(n)]
=DTFT[x(n)*h(n)]=X(e ^ (jw))×H(e ^ (jw))

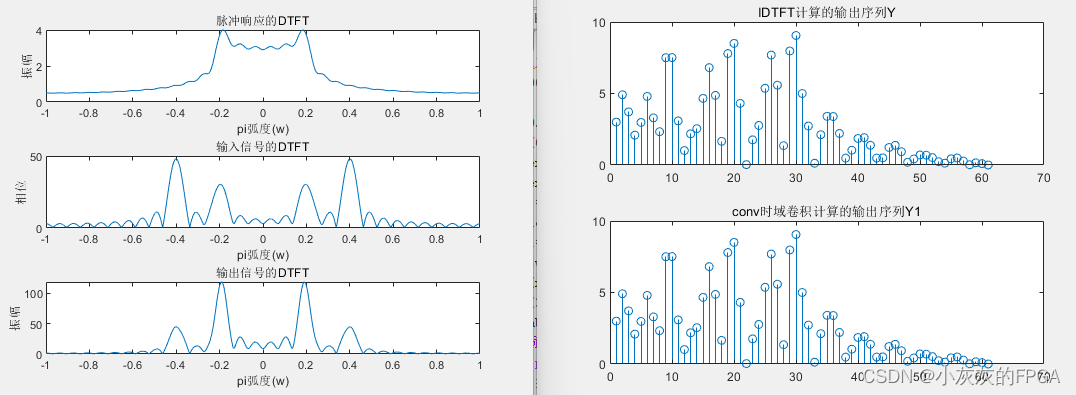
5.Matlab实现DFT和IDFT运算
一个给定离散序列x(n),DFT对应在时域、频域上都是有限长,而且是离散的,该离散序列的DFT和IDFT:
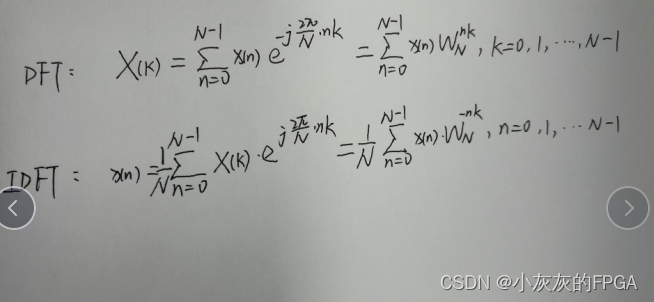
其中W(N)=e^(-j×2π/N)

5、Matlab验证DFT的卷积性质
在Matlab中提供fft函数来计算有限离散序列的DFT。
DFT的循环卷积性质
设序列x(n),h(n)都是N点序列,其DFT分别为X(k),H(k),Y(k)

其中H为循环矩阵,或者循环卷积。
由第1行开始,依次向右移动一个元素,移出去的元素在下一行的最左边出现,即每一行都是h(0),h(N-1),……h(1)这N个元素依次移动生成的。
如果x(n)是M点序列,h(n)是L点序列,y(n)=x(n)*h(n),即y(n)使x(n)和h(n)的线性卷积,y(n)序列的点数为(M+L-1)

toeplitz函数的用法,可以用help toeplitz指令获取帮助。

二、Matlab源码
1、fourier和ifourier函数源码
clear all;
n=0:30;
x=sin(0.2*n).*exp(-0.1*n);
k=0:30;
N=31;
X=x*(exp(-j*2*pi/N).^(n'*k));
subplot(2,1,1);
stem(n,x);
title('x序列');
subplot(2,1,2);
stem(-15:15,[abs(17:end)abs(]);
title('X幅度');
2、Matlab频谱图绘制源码
clear all;
w=-4:0.001:4; %设置频率w的范围,相邻数字频率之间间隔为0.001
n1=-15:15; %h1(n)序列的范围
n2=0:20; %h2(n)序列的范围
h1=exp(-abs(0.1*n1));
h2(n2+1)=1;
Hjw1=h1*(exp(-j*pi).^(n1'*w)); %h1(n)的傅里叶变换
Hjw2=h2*(exp(-j*pi).^(n2'*w)); %h2(n)的傅里叶变换
subplot(2,1,1);
plot(w,abs(Hjw1))
title('h1');
xlabel('pi弧度(w)');
ylabel('振幅');
subplot(2,1,2);
plot(w,abs(Hjw2));
title('h2');
xlabel('pi弧度(w)');
ylabel('振幅');
3、Matlab验证DTFT的频移源码
clear all;
w=-1:0.001:1;
n=0:20;
h(n+1)=1;
x=h.*exp(j*pi*n/4);
y=h.*exp(j*pi*n/2);
Hjw=h*(exp(-j*pi).^(n'*w));
Xjw=x*(exp(-j*pi).^(n'*w));
Yjw=y*(exp(-j*pi).^(n'*w));
subplot(3,2,1);
plot(w,abs(Hjw))
title('H');
xlabel('pi弧度(w)');
ylabel('振幅');
subplot(3,2,2);
plot(w,angle(Hjw)/pi);
title('H');
xlabel('pi弧度(w)');
ylabel('相位');
subplot(3,2,3);
plot(w,abs(Xjw))
title('X');
xlabel('pi弧度(w)');
ylabel('振幅');
subplot(3,2,4);
plot(w,angle(Xjw)/pi);
title('X');
xlabel('pi弧度(w)');
ylabel('相位');
subplot(3,2,5);
plot(w,abs(Yjw))
title('Y');
xlabel('pi弧度(w)');
ylabel('振幅');
subplot(3,2,6);
plot(w,angle(Yjw)/pi);
title('Y');
xlabel('pi弧度(w)');
ylabel('相位');
4、Matlab验证的DTFT卷积性质源码
clear all;
w=-1:0.001:1; %频率w范围,以及间隔为0.001
n=0:30;
h=sinc(0.2*n); %系统的脉冲响应序列
x=2*sin(0.2*pi*n)+3*cos(0.4*pi*n); %系统的输入信号序列
Hjw=h*(exp(-j*pi).^(n'*w)); %脉冲响应的DTFT
Xjw=x*(exp(-j*pi).^(n'*w)); %输入信号的DTFT
Yjw=Xjw.*Hjw; %输出信号的DTFT
n1=0:2*length(n)-2; %输出序列的长度
dw=0.001*pi; %分段求和的步长
y=(dw*Yjw*(exp(j*pi).^(w'*n1)))/(2*pi); %分段求和方式代替积分
y1=conv(x,h); %时序卷积计算
subplot(3,1,1);
plot(w,abs(Hjw))
title('脉冲响应的DTFT');
xlabel('pi弧度(w)');
ylabel('振幅');
subplot(3,1,2);
plot(w,abs(Xjw));
title('输入信号的DTFT');
xlabel('pi弧度(w)');
ylabel('相位');
subplot(3,1,3);
plot(w,abs(Yjw))
title('输出信号的DTFT');
xlabel('pi弧度(w)');
ylabel('振幅');figure
subplot(2,1,1);
stem(abs(y));
title('IDTFT计算的输出序列Y');
subplot(2,1,2);
stem(abs(y1));
title('conv时域卷积计算的输出序列Y1');
5、Matlab实现DFT和IDFT运算
clear all;
n=0:30;
x=sin(0.2*n).*exp(-0.1*n);
k=0:30;
N=31; %离散蓄力DFT的个数
X=x*(exp(-j*2*pi/N).^(n'*k));
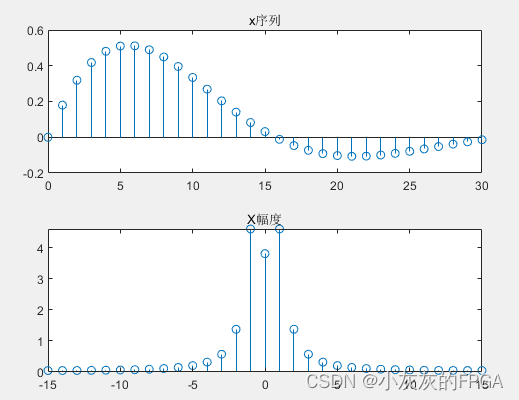
subplot(2,1,1);
stem(n,x);
title('x序列');
subplot(2,1,2);
%验证DFT的对称性,将其范围修改
stem(-15:15,[abs(X(17:end)) abs(X(1:16))]);
title('X幅度');
6、Matlab验证DFT的卷积性质源码clear all;
%矩阵的直接法卷积和DFT
h1=[6 3 4 2 1 -2];
x1=[3 2 4 7 -1 -3];
h2=fliplr(h1); %h1序列反转
H1=toeplitz(h1,[h1(1) h2(1:5)]); %h1序列生成循环矩阵
y=H1*x1'; %根据矩阵定义求解卷积H2=fft(h1); %fft函数求卷积
X1=fft(x1);
Y1=H2.*X1;
y1=ifft(Y1);
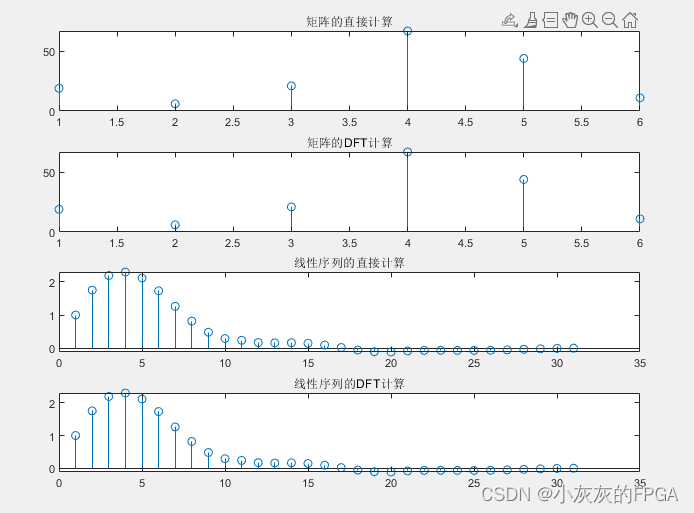
subplot(4,1,1);
stem(y);
title('矩阵的直接计算');
subplot(4,1,2);
stem(y1);
title('矩阵的DFT计算');%线性序列的直接法卷积和DFT
n3=0:20;
n4=0:10;
h3=sinc(0.2*n3);
x3=exp(-0.2*n4);
y3=conv(x3,h3);
%对序列h3和x3补零,构成新的序列h4和x4
h4=[h3 zeros(1,length(x3)-1)];
x4=[x3 zeros(1,length(h3)-1)];
H4=fft(h4);
X4=fft(x4);
Y4=H4.*X4;
y4=ifft(Y4);
subplot(4,1,3);
stem(y3);
title('线性序列的直接计算');
subplot(4,1,4);
stem(y4);
title('线性序列的DFT计算');
这篇关于Matlab通信仿真系列——信号的傅里叶(Fourier)分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







