基于C#实现块状链表

2023-11-27 14:01
文章标签 c# 实现 链表 .net netcore 块状

本文主要是介绍基于C#实现块状链表，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在数据结构的世界里，我们会认识各种各样的数据结构，每一种数据结构都能解决相应领域的问题，当然每个数据结构，有他的优点，必然就有它的缺点，那么如何创造一种数据结构来将某两种数据结构进行扬长避短，那就非常完美了。这样的数据结构也有很多，比如：双端队列，还有就是今天讲的块状链表。
我们都知道
数组 具有 O(1)的查询时间，O(N)的删除，O(N)的插入。。。
链表 具有 O(N)的查询时间，O(1)的删除，O(1)的插入。。。
那么现在我们就有想法了，何不让“链表”和“数组”结合起来，来一起均摊 CURD 的时间，做法将数组进行分块，然后用指针相连接，比如我有 N=100 个元素，那么最理想情况下，我就可以将数组分成 x=10 段，每段 b=10 个元素（排好序），那么我可以用 √N 的时间找到段，因为段中的元素是已经排好序的，所以可以用 lg√N 的时间找到段中的元素，那么最理想的复杂度为 √N+lg√N≈√N。。。
下面我们看看怎么具体使用：

一、结构定义

这个比较简单，我们在每个链表节点中定义一个 头指针，尾指针和一个数组节点。

 public class BlockLinkNode{/// <summary>/// 指向前一个节点的指针/// </summary>public BlockLinkNode prev;/// <summary>/// 指向后一个节点的指针/// </summary>public BlockLinkNode next;/// <summary>/// 链表中的数组/// </summary>public List<int> list;}

二、插入

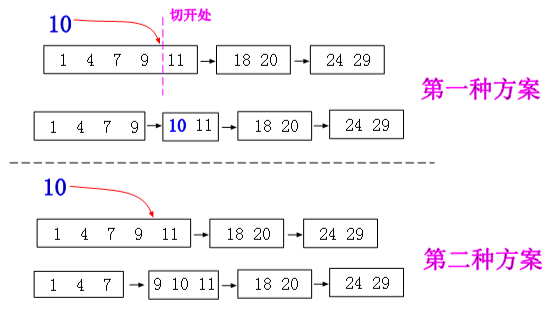
刚才也说了，每个链表节点的数据是一个数组块，那么问题来了，我们是根据什么将数组切开呢？总不能将所有的数据都放在一个链表的节点吧，那就退化成数组了，在理想的情况下，为了保持 √N 的数组个数，所以我们定了一个界限 2√N，当链表中的节点数组的个数超过 2√N 的时候，当下次插入数据的时候，我们有两种做法：

  1. 在元素的数组插入处，将当前数组切开，插入元素处之前为一个链表节点，插入元素后为一个链表节点。
  2. 将元素插入数组后，将数组从中间位置切开。

image.png

 /// <summary>/// 添加元素只会进行块状链表的分裂/// </summary>/// <param name="node"></param>/// <param name="num"></param>/// <returns></returns>private BlockLinkNode Add(BlockLinkNode node, int num){if (node == null){return node;}else{/**  第一步：找到指定的节点*/if (node.list.Count == 0){node.list.Add(num);total = total + 1;return node;}//下一步：再比较是否应该分裂块var blockLen = (int)Math.Ceiling(Math.Sqrt(total)) * 2;//如果该节点的数组的最后位置值大于插入值，则此时我们找到了链表的插入节点，//或者该节点的next=null，说明是最后一个节点，此时也要判断是否要裂开if (node.list[node.list.Count - 1] > num || node.next == null){node.list.Add(num);//最后进行排序下，当然可以用插入排序解决，O(N)搞定node.list = node.list.OrderBy(i => i).ToList();//如果该数组里面的个数大于2*blockLen，说明已经过大了，此时需要对半分裂if (node.list.Count > blockLen){//先将数据插入到数据库var mid = node.list.Count / 2;//分裂处的前段部分var firstList = new List<int>();//分裂后的后段部分var lastList = new List<int>();//可以在插入点处分裂，也可以对半分裂(这里对半分裂)firstList.AddRange(node.list.Take(mid));lastList.AddRange(node.list.Skip(mid).Take(node.list.Count - mid));//开始分裂节点，需要新开辟一个新节点var nNode = new BlockLinkNode();nNode.list = lastList;nNode.next = node.next;nNode.prev = node;//改变当前节点的next和listnode.list = firstList;node.next = nNode;}total = total + 1;return node;}return Add(node.next, num);}}

二、删除

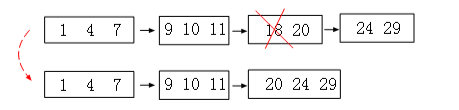
跟插入道理一样，既然有裂开，就有合并，同样也定义了一个界限值 √N /2 ，当链表数组节点的数组个数小于这个界限值的时候，需要将此节点和后面的链表节点进行合并。
image.png

 /// <summary>/// 从块状链表中移除元素,涉及到合并/// </summary>/// <param name="node"></param>/// <param name="num"></param>/// <returns></returns>private BlockLinkNode Remove(BlockLinkNode node, int num){if (node == null){return node;}else{//第一步： 判断删除元素是否在该节点内if (node.list.Count > 0 && num >= node.list[0] && num <= node.list[node.list.Count - 1]){//定义改节点的目的在于防止remove方法假删除的情况发生var prevcount = node.list.Count;node.list.Remove(num);total = total - (prevcount - node.list.Count);//下一步： 判断是否需要合并节点var blockLen = (int)Math.Ceiling(Math.Sqrt(total) / 2);//如果当前节点的数组个数小于 blocklen的话，那么此时改节点需要和后一个节点进行合并//如果该节点时尾节点，则放弃合并if (node.list.Count < blockLen){if (node.next != null){node.list.AddRange(node.next.list);//如果下一个节点的下一个节点不为null，则将下下个节点的prev赋值if (node.next.next != null)node.next.next.prev = node;node.next = node.next.next;}else{//最后一个节点不需要合并，如果list=0，则直接剔除该节点if (node.list.Count == 0){if (node.prev != null)node.prev.next = null;node = null;}}}return node;}return Remove(node.next, num);}}

三、查询

在理想的情况下，我们都控制在 √N，然后就可以用 √N 的时间找到区块，lg√N 的时间找到区块中的指定值，当然也有人在查询的时候做 链表的合并和分裂，这个就有点像伸展树一样，在查询的时候动态调整，拼的是均摊情况下的复杂度。

 public string Get(int num){var blockIndex = 0;var arrIndex = 0;var temp = blockLinkNode;while (temp != null){//判断是否在该区间内if (temp.list.Count > 0 && num >= temp.list[0] && num <= temp.list[temp.list.Count - 1]){arrIndex = temp.list.IndexOf(num);return string.Format("当前数据在第{0}块中的{1}个位置", blockIndex, arrIndex);}blockIndex = blockIndex + 1;temp = temp.next;}return string.Empty;}

好了，CURD 都分析好了，到这里大家应该对 块状链表有个大概的认识了吧，这个代码是我下午抽闲写的，没有仔细测试，最后是总的代码：

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;namespace ConsoleApplication3
{class Program{static void Main(string[] args){List<int> list = new List<int>() { 8959, 30290, 18854, 7418, 28749, 17313, 5877, 27208, 15771, 4335 };//list.Clear();//List<int> list = new List<int>();//for (int i = 0; i < 100; i++)//{//    var num = new Random((int)DateTime.Now.Ticks).Next(0, short.MaxValue);//    System.Threading.Thread.Sleep(1);//    list.Add(num);//}BlockLinkList blockList = new BlockLinkList();foreach (var item in list){blockList.Add(item);}//var b = blockList.IsExist(333);//blockList.GetCount();Console.WriteLine(blockList.Get(27208));#region MyRegion随机删除150个元素//for (int i = 0; i < 5000; i++)//{//    var rand = new Random((int)DateTime.Now.Ticks).Next(0, list.Count);//    System.Threading.Thread.Sleep(2);//    Console.WriteLine("\n**************************************\n当前要删除元素：{0}", list[rand]);//    blockList.Remove(list[rand]);//    Console.WriteLine("\n\n");//    if (blockList.GetCount() == 0)//    {//        Console.Read();//        return;//    }//} #endregionConsole.Read();}}public class BlockLinkList{BlockLinkNode blockLinkNode = null;public BlockLinkList(){//初始化节点blockLinkNode = new BlockLinkNode(){list = new List<int>(),next = null,prev = null};}/// <summary>/// 定义块状链表的总长度/// </summary>private int total;public class BlockLinkNode{/// <summary>/// 指向前一个节点的指针/// </summary>public BlockLinkNode prev;/// <summary>/// 指向后一个节点的指针/// </summary>public BlockLinkNode next;/// <summary>/// 链表中的数组/// </summary>public List<int> list;}/// <summary>/// 判断指定元素是否存在/// </summary>/// <param name="num"></param>/// <returns></returns>public bool IsExist(int num){var isExist = false;var temp = blockLinkNode;while (temp != null){//判断是否在该区间内if (temp.list.Count > 0 && num >= temp.list[0] && num <= temp.list[temp.list.Count - 1]){isExist = temp.list.IndexOf(num) > 0 ? true : false;return isExist;}temp = temp.next;}return isExist;}public string Get(int num){var blockIndex = 0;var arrIndex = 0;var temp = blockLinkNode;while (temp != null){//判断是否在该区间内if (temp.list.Count > 0 && num >= temp.list[0] && num <= temp.list[temp.list.Count - 1]){arrIndex = temp.list.IndexOf(num);return string.Format("当前数据在第{0}块中的{1}个位置", blockIndex, arrIndex);}blockIndex = blockIndex + 1;temp = temp.next;}return string.Empty;}/// <summary>/// 将元素加入到块状链表中/// </summary>/// <param name="num"></param>public BlockLinkNode Add(int num){return Add(blockLinkNode, num);}/// <summary>/// 添加元素只会进行块状链表的分裂/// </summary>/// <param name="node"></param>/// <param name="num"></param>/// <returns></returns>private BlockLinkNode Add(BlockLinkNode node, int num){if (node == null){return node;}else{/**  第一步：找到指定的节点*/if (node.list.Count == 0){node.list.Add(num);total = total + 1;return node;}//下一步：再比较是否应该分裂块var blockLen = (int)Math.Ceiling(Math.Sqrt(total)) * 2;//如果该节点的数组的最后位置值大于插入值，则此时我们找到了链表的插入节点，//或者该节点的next=null，说明是最后一个节点，此时也要判断是否要裂开if (node.list[node.list.Count - 1] > num || node.next == null){node.list.Add(num);//最后进行排序下，当然可以用插入排序解决，O(N)搞定node.list = node.list.OrderBy(i => i).ToList();//如果该数组里面的个数大于2*blockLen，说明已经过大了，此时需要对半分裂if (node.list.Count > blockLen){//先将数据插入到数据库var mid = node.list.Count / 2;//分裂处的前段部分var firstList = new List<int>();//分裂后的后段部分var lastList = new List<int>();//可以在插入点处分裂，也可以对半分裂(这里对半分裂)firstList.AddRange(node.list.Take(mid));lastList.AddRange(node.list.Skip(mid).Take(node.list.Count - mid));//开始分裂节点，需要新开辟一个新节点var nNode = new BlockLinkNode();nNode.list = lastList;nNode.next = node.next;nNode.prev = node;//改变当前节点的next和listnode.list = firstList;node.next = nNode;}total = total + 1;return node;}return Add(node.next, num);}}/// <summary>/// 从块状链表中移除元素/// </summary>/// <param name="num"></param>/// <returns></returns>public BlockLinkNode Remove(int num){return Remove(blockLinkNode, num);}/// <summary>/// 从块状链表中移除元素,涉及到合并/// </summary>/// <param name="node"></param>/// <param name="num"></param>/// <returns></returns>private BlockLinkNode Remove(BlockLinkNode node, int num){if (node == null){return node;}else{//第一步： 判断删除元素是否在该节点内if (node.list.Count > 0 && num >= node.list[0] && num <= node.list[node.list.Count - 1]){//定义改节点的目的在于防止remove方法假删除的情况发生var prevcount = node.list.Count;node.list.Remove(num);total = total - (prevcount - node.list.Count);//下一步： 判断是否需要合并节点var blockLen = (int)Math.Ceiling(Math.Sqrt(total) / 2);//如果当前节点的数组个数小于 blocklen的话，那么此时改节点需要和后一个节点进行合并//如果该节点时尾节点，则放弃合并if (node.list.Count < blockLen){if (node.next != null){node.list.AddRange(node.next.list);//如果下一个节点的下一个节点不为null，则将下下个节点的prev赋值if (node.next.next != null)node.next.next.prev = node;node.next = node.next.next;}else{//最后一个节点不需要合并，如果list=0，则直接剔除该节点if (node.list.Count == 0){if (node.prev != null)node.prev.next = null;node = null;}}}return node;}return Remove(node.next, num);}}/// <summary>/// 获取块状链表中的所有个数/// </summary>/// <returns></returns>public int GetCount(){int count = 0;var temp = blockLinkNode;Console.Write("各节点数据个数为：");while (temp != null){count += temp.list.Count;Console.Write(temp.list.Count + ",");temp = temp.next;}Console.WriteLine("总共有:{0} 个元素", count);return count;}}}

这篇关于基于C#实现块状链表的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/427812。

相关文章

Python使用Tenacity一行代码实现自动重试详解

Python使用Tenacity一行代码实现自动重试详解

《Python使用Tenacity一行代码实现自动重试详解》tenacity是一个专为Python设计的通用重试库,它的核心理念就是用简单、清晰的方式,为任何可能失败的操作添加重试能力,下面我们就来看... 目录一切始于一个简单的 API 调用Tenacity 入门：一行代码实现优雅重试精细控制：让重试按我
阅读更多...
Redis客户端连接机制的实现方案

Redis客户端连接机制的实现方案

《Redis客户端连接机制的实现方案》本文主要介绍了Redis客户端连接机制的实现方案,包括事件驱动模型、非阻塞I/O处理、连接池应用及配置优化,具有一定的参考价值,感兴趣的可以了解一下... 目录1. Redis连接模型概述2. 连接建立过程详解2.1 连php接初始化流程2.2 关键配置参数3. 最大连
阅读更多...
Python实现网格交易策略的过程

Python实现网格交易策略的过程

《Python实现网格交易策略的过程》本文讲解Python网格交易策略,利用ccxt获取加密货币数据及backtrader回测,通过设定网格节点,低买高卖获利,适合震荡行情,下面跟我一起看看我们的第一... 网格交易是一种经典的量化交易策略，其核心思想是在价格上下预设多个“网格”，当价格触发特定网格时执行买
阅读更多...
python设置环境变量路径实现过程

python设置环境变量路径实现过程

《python设置环境变量路径实现过程》本文介绍设置Python路径的多种方法：临时设置（Windows用`set`,Linux/macOS用`export`）、永久设置（系统属性或shell配置文件... 目录设置python路径的方法临时设置环境变量（适用于当前会话）永久设置环境变量（Windows系统
阅读更多...
Python对接支付宝支付之使用AliPay实现的详细操作指南

Python对接支付宝支付之使用AliPay实现的详细操作指南

《Python对接支付宝支付之使用AliPay实现的详细操作指南》支付宝没有提供PythonSDK,但是强大的github就有提供python-alipay-sdk,封装里很多复杂操作,使用这个我们就... 目录一、引言二、准备工作2.1 支付宝开放平台入驻与应用创建2.2 密钥生成与配置2.3 安装ali
阅读更多...
Spring Security 单点登录与自动登录机制的实现原理

Spring Security 单点登录与自动登录机制的实现原理

《SpringSecurity单点登录与自动登录机制的实现原理》本文探讨SpringSecurity实现单点登录（SSO）与自动登录机制,涵盖JWT跨系统认证、RememberMe持久化Token... 目录一、核心概念解析1.1 单点登录（SSO）1.2 自动登录（Remember Me）二、代码分析三、
阅读更多...
C#中lock关键字的使用小结

C#中lock关键字的使用小结

《C#中lock关键字的使用小结》在C#中,lock关键字用于确保当一个线程位于给定实例的代码块中时,其他线程无法访问同一实例的该代码块,下面就来介绍一下lock关键字的使用... 目录使用方式工作原理注意事项示例代码为什么不能lock值类型在C#中，lock关键字用于确保当一个线程位于给定实例的代码块中时
阅读更多...
C# $字符串插值的使用

C# $字符串插值的使用

《C#$字符串插值的使用》本文介绍了C#中的字符串插值功能,详细介绍了使用$符号的实现方式,文中通过示例代码介绍的非常详细,需要的朋友们下面随着小编来一起学习学习吧... 目录$ 字符使用方式创建内插字符串包含不同的数据类型控制内插表达式的格式控制内插表达式的对齐方式内插表达式中使用转义序列内插表达式中使用
阅读更多...
C#中的Converter的具体应用

C#中的Converter的具体应用

《C#中的Converter的具体应用》C#中的Converter提供了一种灵活的类型转换机制,本文详细介绍了Converter的基本概念、使用场景,具有一定的参考价值,感兴趣的可以了解一下... 目录Converter的基本概念1. Converter委托2. 使用场景布尔型转换示例示例1：简单的字符串到
阅读更多...
PyCharm中配置PyQt的实现步骤

PyCharm中配置PyQt的实现步骤

《PyCharm中配置PyQt的实现步骤》PyCharm是JetBrains推出的一款强大的PythonIDE,结合PyQt可以进行pythion高效开发桌面GUI应用程序,本文就来介绍一下PyCha... 目录1. 安装China编程PyQt1.PyQt 核心组件2. 基础 PyQt 应用程序结构3. 使用 Q
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2