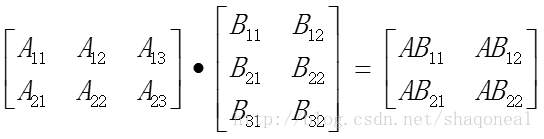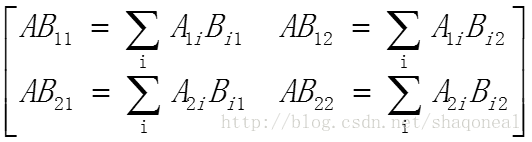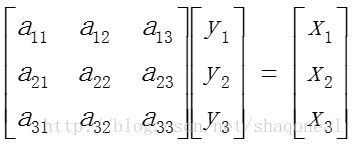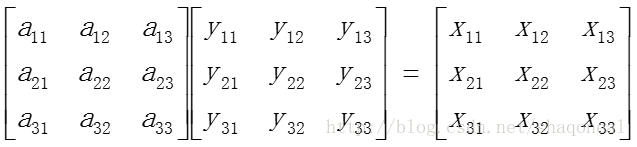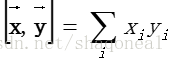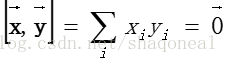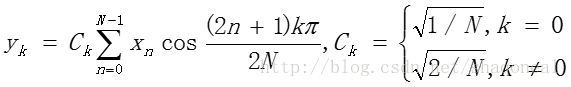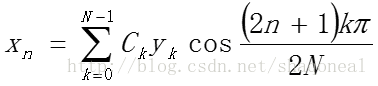本文主要是介绍【H.264/AVC视频编解码技术详解】十四、H.264的变换编码(一)——矩阵运算与正交变换基本概念,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
《H.264/AVC视频编解码技术详解》视频教程已经在“CSDN学院”上线,视频中详述了H.264的背景、标准协议和实现,并通过一个实战工程的形式对H.264的标准进行解析和实现,欢迎观看!
“纸上得来终觉浅,绝知此事要躬行”,只有自己按照标准文档以代码的形式操作一遍,才能对视频压缩编码标准的思想和方法有足够深刻的理解和体会!
链接地址:H.264/AVC视频编解码技术详解
GitHub代码地址:点击这里
1. 矩阵的定义
矩阵,英文称为"Matrix",是数学中一个非常重要的概念。从形式上看,矩阵可以用一个m行n列的数组成的表格表示。如下图可表示一个4行4列的方形矩阵:

在实际应用中,矩阵可以在多个技术领域发挥重要作用,如音视频压缩编码、机器学习、人工智能等领域。

2. 矩阵的运算
矩阵必须在计算中才能与其他数据进行交互。在《线性代数》中我们已经清楚地知道,矩阵可以进行求和、数乘和与矩阵相乘等运算。其中矩阵的求和与数乘运算十分简单:
- 矩阵求和:同型矩阵可以求和,即将对应元素求和组成新的矩阵;
- 矩阵数乘:任何矩阵都可与实数相乘,即将每个元素与该数字相乘组成新的矩阵;
而相比之下,矩阵与矩阵相乘会略显复杂,需要满足必要条件,即矩阵1的宽必须等于矩阵2的高方可相乘。乘积矩阵的高和宽分别为矩阵1的高和矩阵2的宽,如下图表示:
其中,乘积矩阵的元素的计算方法为:
通常,我们将只有一行或一列的矩阵称之为向量。根据排列的不同,按行或列排列的向量分别称之为行向量和列向量。
3. 向量和矩阵的线性变换
向量的线性变换定义为:向量y的每一个元素都是向量x中元素的线性组合,则y是x的线性变换。假设有向量[x1, x2, x3]和向量[y1, y2, y3],两个向量满足以下关系:
- y1 = a11 * x1 + a12 * x2 + a13 * x3
- y2 = a21 * x1 + a22 * x2 + a23 * x3
- y3 = a31 * x1 + a32 * x2 + a33 * x3
那么我们称向量[y1, y2, y3]可以被向量[x1, x2, x3]线性表示,以公式形式则表示为y=A·x。其含义可表示为矩阵与向量相乘:
矩阵A即为该线性变换的矩阵。
将向量的变换推广,矩阵可以视为由向量构成,因此线性线性变换同样适用于矩阵的变换:
4. 向量的正交性、正交矩阵和正交变换
要了解向量的正交性,首先应了解向量的内积的概念。在“不严格”的条件下,我们暂且可以将向量的内积理解为数量积,即两个相同长度向量对应元素乘积的总和。用公式表示为:
而向量的正交,等价于两个向量的内积为0。即:
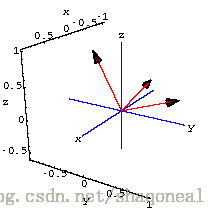
在二维和三维空间内直观地表示,两个正交向量相互垂直:
由于矩阵可视为由多个列向量构成,那么多个两两正交的向量可以构成正交矩阵。一个矩阵是正交矩阵需要满足的条件有:
- 行数和列数相等,即正交矩阵都为方阵;
- 每一个列向量均为单位向量,即长度均为1;
- 各列向量两两正交;
前面提到,每一个矩阵都可以与一个线性变换对应。那么如果一个线性变换对应的变换矩阵是正交矩阵,那么该变换就是一个正交变换。正交变换的显著特点之一是,向量经过正交变换后长度不会发生变化。
5. 离散余弦变换
离散余弦变换 (Discrete Cosine Transform, DCT)类似于一种实数类型的离散傅里叶变换(DFT),其定义有多种形式(可参考维基百科:离散余弦变换)。常用场合中使用的离散余弦变换是一个正交变换,其正变换和逆变换的计算方法如:
由于DCT具有类似于DFT的特性,DCT也可以实现如信息能量集中的功能。对于图像数据,DCT可以有效将大部分的能量集中与直流和低频部分,这也成为视频压缩中变换编码的理论基础之一。实际上,DCT长期应用与多种图像和视频的压缩编码标准中:
- 视频:MPEG-1/MPEG-2;
- 图像:JPEG
在H.264及更新的视频压缩标准中,采用的是DCT的优化改进版——整数变换。相对于浮点类型的离散余弦变换,整数变换有效降低了变换操作的运算复杂度,提升了编解码器的运行效率。
这篇关于【H.264/AVC视频编解码技术详解】十四、H.264的变换编码(一)——矩阵运算与正交变换基本概念的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!