cs224w 图神经网络 学习笔记（七）Message Passing and Node Classification 信息传播与节点分类

课程链接：CS224W: Machine Learning with Graphs
课程视频：【课程】斯坦福 CS224W: 图机器学习 (2019 秋 | 英字)

1. 前言

这节课需要解决的问题是：Given a network with labels on some nodes, how do we assign labels to all other nodes in the network? 给定一个网络，网络上的部分节点打好了标签，如何给剩下的节点分配标签？——节点分类问题。

对于这个问题，我们从网络中的“相关性（Correlations）”开始。首先，先介绍图节点分类的思想——Collective classification，然后介绍三种分类的算法：

• Relational classification
• Iterative classification
• Belief propagation 置信度传播算法

节点分类被应用于很多领域，如：Document classification（文献分类）、Part of speech tagging（词性标注）、Link prediction（链路预测）、Optical character recognition（OCR识别）、Image/3D data segmentation （图像/三维数据分割）、Entity resolution in sensor networks、Spam and fraud detection（垃圾邮件和欺诈检测）等。

2. 图节点分类的思想——Collective classification

2.1 概述

Correlations exist in networks——网络中天生就存在关系。我们先从社交网络看起，个人行为和外部环境的影响是息息相关的，主要有以下三种类型的关系：

Homophily 同质性	Influence 影响型	Confounding 混合型
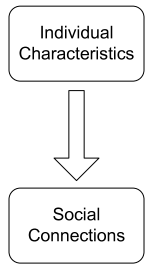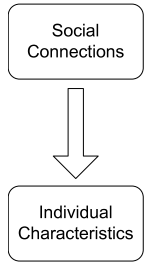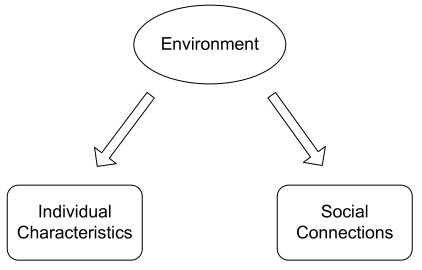物以类聚，人以群分	橘生淮南则为橘，橘生淮北则为枳	时势造英雄，英雄造时势

对节点进行分类的一个很重要的想法就是：Guit-by-association——Similar nodes are typically close together or directly connected （相似的节点通常紧密相连或直接连接）。节点$O$的标签（分类）取决于以下三个因素：

• Features of $O$ 节点$O$的特征
• Labels of the objects in $O$'s neighborhood 节点$O$的邻居节点的标签
• Features of the objects in $O$'s neighborhood 节点$O$的邻居节点的特征

因此，我们可以将问题进行更加数学化的描述：定义$n\times n$矩阵$W$为图$G$的邻接矩阵；定义向量 Y = { − 1 , 0 , 1 } n Y=\{-1,0,1\}^n Y={−1,0,1}n表示$n$个节点的标签，由于这里只考虑二分类问题，$y_i=0$为unlabeled node，是待分类的节点，$y_i=1$为positive node，$y_i=-1$为negtive node。我们需要解决的问题就是unlabeled node中有多少个节点大概率是positive node。

我们引入Markov Assumption（马尔科夫假设）来描述这种内在联系的思想：
$$P(Y_i|i)=P(Y_i|N_i)$$

那么，整个问题就转变成计算未知节点$i$的标签为$Y_i$的概率：

总的来说collective classification包括三个步骤：

（1）Local classifier——用于给节点分配初始标签

• 通过节点的属性/特点预测节点标签
• 是一个标准分类任务
• 因为没有用到网络信息，所以是“本地分类器”

（2）Relational Classifier——基于网络（结构）捕捉节点之间的关系

• 学习一个分类器，基于节点自身及其邻居节点的属性/特征对节点进行分类
• 在这一步会使用到网络的信息

（3）Collective Inference——通过网络传播相关性

• 将Relational Classifier迭代应用于每个节点，直到相邻节点的非一致性最小化为止
• 实质上，网络的结构会影响到最终的预测

需要说明的是，要精确地完成这些步骤进行推理一个NP难度的问题，只有在网络结构满足特定的条件时，才能得到最精确的结果。所以，在实际应用中，我们主要关注的是近似解法——Relational classifiers/ Iterative classification/ Belief propagation。这些算法都是迭代算法（iterative algorithms）。

2.2 Probabilistic Relational Classifier

基本思想：Class probability of $Y_i$ is a weighted average of class probabilities of its neighbors. $P(Y_i)$是其邻居节点的标签为$Y_i$的加权平均。对于已经有标签的节点，其$Y$值就是其真实的标签；对于没有标签的节点，将其$Y$值统一进行初始化。按随机顺序更新所有节点，直到收敛或达到最大迭代次数。

对每个节点$i$及其标签$c$，重复进行如下运算（加权平均，权重应该是表示邻居节点对其的影响）：
$$P(Y_i=c)=\frac{1}{{\sum }_{(i,j)\in E}W(i,j)}\sum _{(i,j)\in E}W(i,j)P(Y_j=c)$$
其中$W(i,j)$表示从节点$i$到节点$j$的权重。

下面通过一个例子来感受一下这个算法：

步骤	具体操作	例子
初始化	对于已经有标签的节点，其$Y$值就是其真实的标签；对于没有标签的节点，将其$Y$值统一进行初始化。
第一轮迭代	随机选择节点3， N 3 = { 1 , 2 , 4 } N_3=\{1,2,4\} N3​={1,2,4}，则$P(Y=1$|$N_3)=\frac{1}{3}(0+0+0.5)=0.17$
第一轮迭代	随机选择节点4， N 4 = { 1 , 3 , 5 , 6 } N_4=\{1,3,5,6\} N4​={1,3,5,6}，需要注意的是此时节点3的$P(Y=1)=0.17$
第一轮迭代	随机选择节点5， N 5 = { 4 , 6 , 7 , 8 } N_5=\{4,6,7,8\} N5​={4,6,7,8}
第一轮迭代结束
第二轮迭代结束
第三轮迭代结束
第四轮迭代结束
五次迭代后，网络趋于稳定

不过，Probabilistic Relational Classifier算法有两个不足：第一，算法并不能保证收敛；第二，该算法模型并没有使用节点信息。

2.3 Iterative classification

基本思想

通过节点$i$自身的属性及其邻居节点的标签来进行分类。首先，对每个节点$i$，定义一个平面向量${\alpha }_i$；接着，训练一个基于向量${\alpha }_i$的分类器；每个节点都有不同数量的邻居，我们可以根据下面这些指标再进一步进行聚类（aggregate）——count （数量）, mode（模式）, proportion（比例）,mean（均值）, exists（存在性）, 等等。

基本架构
（1）Bootstrap phase

• 将每个节点$i$转换成平面向量${\alpha }_i$
• 使用局部分类器$f({\alpha }_i)$（例如SVM、kNN等）来得到$Y_i$的最佳值

（2）Iteration phase——迭代直至收敛

• 对每个节点$i$重复以下操作：更新节点向量${\alpha }_i$，根据局部分类器$f({\alpha }_i)$更新$Y_i$的值。
• 迭代直到标签稳定或达到最大迭代次数

需要指出的是，Iterative classification算法同样不能保证收敛，一般会设置最大迭代次数最为迭代终止的条件。

2.4 Loopy belief propagation 环路置信传播

Belief Propagation 算法（BP算法）是将概率论应用到图结构中的一种动态规划的算法。在迭代过程中，相邻的节点相互交换“信息”（passing message）。当相邻节点“达成共识（When consensus is reached）”，计算最后的置信值（belief）。

BP算法解决的第一个任务就是传递信息（message passing），传递信息的一个原则是每个节点值接收或传递其邻居节点的信息。

图的样式	传递模式
straight line graph（直线图），每个节点只接收传入的消息
Tree（树结构），每个节点从树的所有分支接收信息

但是，这样的方法无法用于带环的图。

我们再来看一下信息传递的定义——节点$i$给节点$j$传递的信息取决于节点$i$的所有邻居节点$k$传递给节点$i$的信息以及每个邻居节点$k$对节点$i$目前的置信状态的影响。

为此，我们定义以下符号：

• Label-label potential matrix $\psi$，表示节点与其邻居之间的依赖关系。${\psi }_{(}{Y}_i,Y_j)$为给定节点$i$处的状态为$Y_i$的情况下，节点$j$处状态为$Y_j$的可能性，即$P(Y_j|Y_i)$。
• Prior belief $\varphi$，${\varphi }_i(Y_i)$表示节点$i$处于状态$Y_i$的可能性。
• $m_{i\to j}(Y_i)$表示节点$i$对节点$j$处于状态$Y_j$的估计
• $\mathcal{L}$是所有状态的集合

Loopy BP算法的步骤如下：

（1）首先将所有的信息初始化为1。

（2）对每个节点重复以下操作：

$$m_{i\to j}(Y_i)=\alpha \sum _{Y_i\in \mathcal{L}}\psi (Y_i,Y_j){\varphi }_i(Y_i)\prod _{k\in {\mathcal{N}}_i\setminus j}{m}_{k\to i}(Y_i)$$

（3）收敛后，可以通过下面这个式子计算节点$i$处于状态$Y_i$的置信度：

最后是Loopy BP算法的一些优缺点：