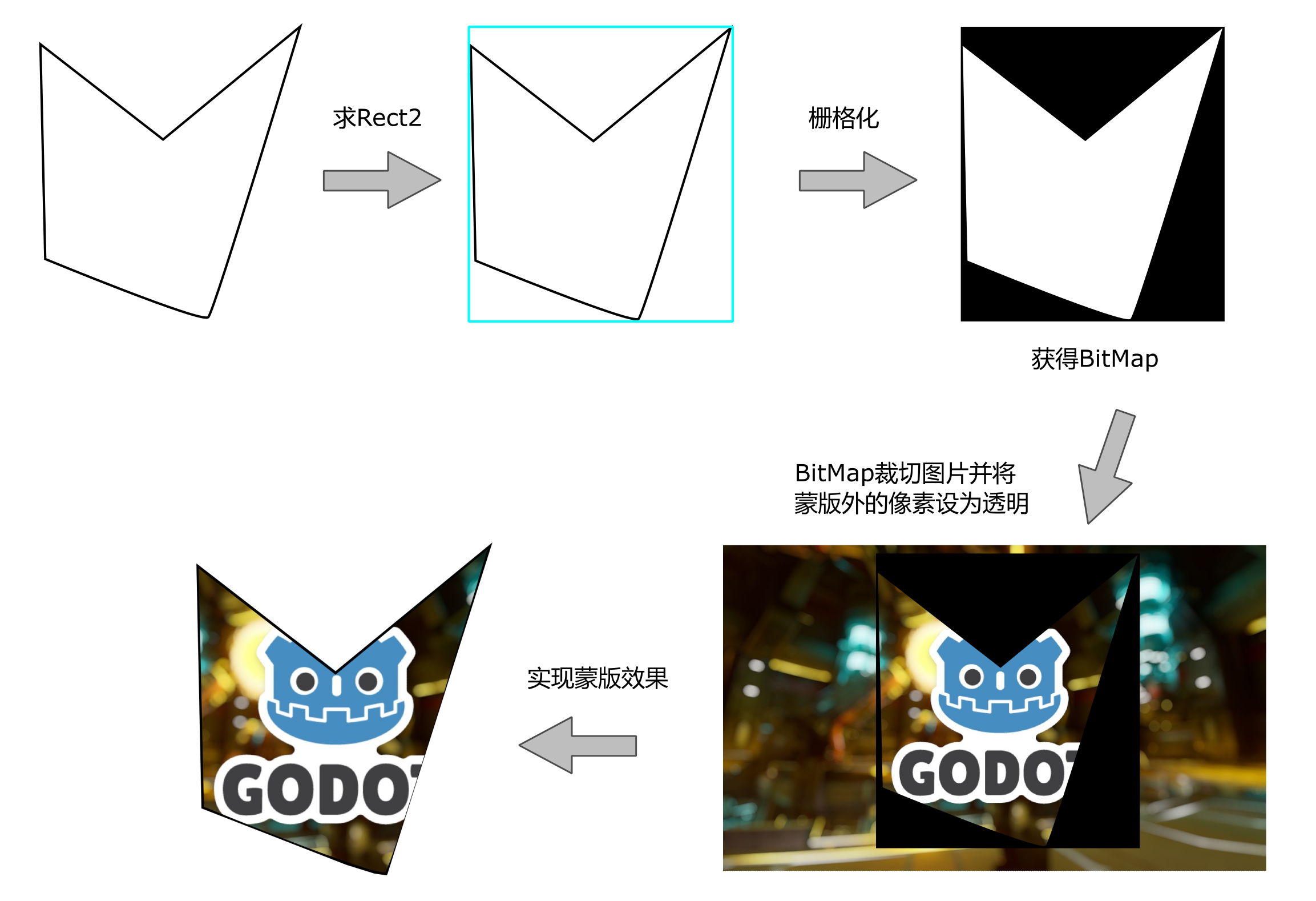
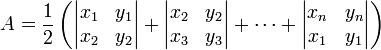本文主要是介绍多边形求交并差,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
代码:Github:team79/PolygonOverlayAnalysis
基本概念介绍
多边形交并差计算的算法的相关证明过程是很繁琐,因此在这里将直接给出算法所需的概念以及算法所用到的一些性质。具体的相关证明过程在ZHU Ya-Yin[1]论文中有详细证明。
算法中的一些概念:
- 1、∂A :多边形A 的边的集合, 或A 的边界上点的集合;
- 2、P ↓:过点P 作的垂直向下射线;
- 3、<:点的小于比较符, P < Q (Px < Qx )∨(Px =Qx ∧ Py < Qy);
- 4、P x , Py :P 的横、纵坐标;
- 5、Lp(e):e 的左端点, 即e 两端点中较小的一个;
- 6、Rp(e):e 的右端点, 即e 两端点中较大的一个;
- 7、I(e):e 内点(e 上除端点外的其他点)的集合;
- 8、e , s :边;
- 9、C(P ,∂ A):与P ↓有交点, 且右端点不在P ↓上的A 的边集合.即C(P , ∂A)={s s ∈ A , s ∩P ↓≠ , R p(s) P ↓};
- 10、s1 >P s2 :边s1 , s2 在通过P 点的垂直线x =Px上的比较, 即s1 >P s2 (Q1 >Q2)∨ (Q1 =Q2 ∧Ks1 >Ks2), 其中点Q1 , Q2 表示边s1 , s2 与过P 点的垂线的交点, Ks1 , Ks2 分别表示s1 , s2 的斜率;
- 11、max(C(P , ∂A)):表示C(P , ∂A)中在P 点处的最大边。
算法所用到的定理与性质:
- 1、对于多边形A 的任一条边,设P是e的内点, 如果C(P , ∂A)有奇数条边, 则称e是A的奇边, 简记为+e,否则称e是A的偶边,简记为-e;
- 2、对于任意两条边s1 , s2 ∈ C(P ,∂ A), 如果s2 是在P 点处小于s1 的最大边, 即s1 >P s2 , 且不存在边e ∈ C(P ,∂ A), 使得s1 >P e , e >P s2 同时成立, 则s1 , s2 在A 中的奇偶相异;
- 3、对于任一不在多边形A 边界上的点P , 如果过点P 所作的垂直向下的射线与多边形A
的相交的最大边是偶边, 或没有与A 的任何边相交, 则P 在多边形A 的外域, 其逆亦然;如果射线与A 相交的最大边是奇边, 则P 在多边形A 的内域,其逆亦然; - 4、内边:e 的所有内点均位于A 的内域, P , P∈ I(e) P ∈ I (A);
- 5、外边:e 的所有内点均位于A 的外域, P , P∈ I(e) P ∈ E(A);
- 6、重叠边: s , s ∈ A , P , P ∈ e P ∈ s;
- 7、简单边:内边、外边、重叠边;
- 8、复杂边:不属于简单边的其他边。
算法总体流程
算法整体步骤如下:
- Setp1 .在平面扫描过程中, 计算A , B 的交点(包括切点), 分解复杂边为简单边, 同时根据算法1 , 2 , 确定A , B 边的奇偶性及其拓扑类型, 并记录在数据结构中;
- Setp2 .针对多边形交、并、差的具体计算特点,分别根据算法2-11、2-12、2-13进行边的跟踪, 输出构成A ∩B , A ∪ B , A -B 的中间多边形;
- Setp3 .依次构造各中间多边形的Border , 确定中间多边形的方向性.根据定理与性质判断其是洞还是外接多边形;
- Setp4 .判断洞Border 与外接多边形Border 的包含被包含关系, 确定洞归属于哪个外接多边形, 进而确定A ∩ B , A ∪ B , A -B.
多边形求交算法
多边形求交的伪代码表示如下表:
I for each e of A , B 的边{
II if e 没有访问过∧ (e 是内边∨ )then
III do{
IV 标记e 为已访问;如果e 是重叠边, 还要标记其重叠边e′为已访问;
V if e 是奇边then {
VI 把e 的左端点添加到顶点链表中;
VII P →e 的右端点;
VIII }else {∥隐含条件e 是偶边
IX 把e 的右端点添加到顶点链表中;
X P →e 的左端点;
XI }
XII if (在连接P 的另一输入多边形的邻边中, 存在着满足条件的内边s :
XIII s 是奇边且P =Lp(s), 或者s 是偶边且P =Rp(s))then e →s ;
XIV else e →连接P 的本输入多边形的邻边;
XV }until P 与顶点链表中的第1 个顶点相等;
XVI 输出顶点链表中顶点组成的中间多边形, 并清空顶点链表;
XVII } ∥end if
XVIII} ∥end fo r多边形求并算法
多边形求并的伪代码表示如下表:
I for each e of A , B 的边{
II if e 没有访问过∧ (e 是外边∨ )then
III do{
IV 标记e 为已访问;如果e 是重叠边, 还要标记其重叠边e′为已访问;
V if e 是奇边then {
VI 把e 的左端点添加到顶点链表中;
VII P →e 的右端点;
VIII }else {∥隐含条件e 是偶边
IX 把e 的右端点添加到顶点链表中;
X P →e 的左端点;
XI }
XII if 连接P 的本输入多边形的邻边s 是外边then e→s;
XIII else if 连接P 的另一输入多边形的邻边中, 存在着外边s′then e →s′.
XIV else e →连接P 的本输入多边形的邻边;
XV }until P 与顶点链表中的第1 个顶点相等;
XVI 输出顶点链表中顶点组成的中间多边形, 并清空顶点链表;
XVII } ∥end if
XVIII} ∥end fo r多边形求差算法
多边形求差的伪代码表示如下表:
I for each e of A , B 的边{
II if e 没有访问过∧ ((e 是A 的外边)∨ (e 是B 的内边))then {
III do{
IV 记e 为已访问;如果e 是重叠边, 还要标记其重叠边e′为已访问;
V if e 是A 的奇边或是B 的偶边then {
VI 把e 的左端点添加到顶点链表中;
VII P →e 的右端点;
VIII }else {∥隐含条件:e 是A 的偶边或是B 的奇边
IX 把e 的右端点添加到顶点链表中;
X P →e 的左端点;
XI }
XII if e 是A 的边, 与P 相连的属于B 的邻边中, 存在着满足条件的内边s:s 是B 的奇边且P 是s的右端点, 或者s 是偶边且P 是s 的左端点then e →s ;
XII else if e 是B 的边, 与P 相连的属于A 的邻边中, 存在着满足条件的外边s′:s′是奇边且P 是s′的左端点, 或s′是偶边且P 是s′的右端点then e →s′
XIV else e →连接P 的本输入多边形的邻边;
XV }until P 与顶点链表中的第1 个顶点相等;
XVI 输出顶点链表中顶点组成的中间多边形, 并清空顶点链表;
XVII } ∥end if
XVIII} ∥end fo r多边形:
交:
并:
差:
这篇关于多边形求交并差的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!