本文主要是介绍2020-6-3 吴恩达-改善深层NN-w2 优化算法(2.7 RMSprop -消除梯度下降中的摆动,加速下降,加快学习 -和动量异同点),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.视频网站:mooc慕课https://mooc.study.163.com/university/deeplearning_ai#/c
2.详细笔记网站(中文):http://www.ai-start.com/dl2017/
3.github课件+作业+答案:https://github.com/stormstone/deeplearning.ai
2.7 RMSprop
RMSprop的算法,全称root mean square prop算法,它也可以加速梯度下降。

观察上图。上节课已经介绍过,传统或者mini-batch梯度下降过程,虽然横轴方向正在推进,但纵轴方向会有大幅度摆动。
为了分析这个例子,假设纵轴代表参数 b b b,横轴代表参数 W W W,可能有 W 1 W_1 W1, W 2 W_2 W2或者其它重要的参数,为了便于理解,被称为 b b b 和 W W W。
所以,为了加速下降,加速学习过程,类似动量梯度下降法,你想减缓纵轴 b b b 方向的学习。同时加快,至少不是减缓横轴 W W W 方向的学习,RMSprop算法可以实现这一点。
和动量梯度下降法一样,RMSprop算法会照常计算当下mini-batch的微分 d W dW dW 和 d b db db。
RMSprop算法中使用的指数加权平均数符号是 S d W S_{dW} SdW 和 S d b S_{db} Sdb。而动量梯度下降法使用的是 v d W v_{dW} vdW 和 v d b v_{db} vdb
公式如下
- S d W = β S d W + ( 1 − β ) d W 2 S_{dW}=\beta S_{dW}+(1-\beta) dW^2 SdW=βSdW+(1−β)dW2
- S d b = β S d b + ( 1 − β ) d b 2 S_{db}=\beta S_{db}+(1-\beta) db^2 Sdb=βSdb+(1−β)db2
说明
- 这是使用的是微分平方的加权平均数
- 平方是针对整个符号 d W dW dW 和 d b db db 的操作
RMSprop会按照如下方式更新参数值
- W : = W − α d W S d W W := W - \alpha \frac {dW}{\sqrt {S_{dW}}} W:=W−αSdWdW
- b : = b − α d b S d b b := b - \alpha \frac {db}{\sqrt {S_{db}}} b:=b−αSdbdb
解释一下原理
我们已经说过,要加速梯度下降速度,在横轴方向,我们希望学习速度快,而在垂直方向,我们希望减缓纵轴上的摆动,所以有了梯度加权平均(也就是要考虑历史梯度影响) S d W S_{dW} SdW 和 S d b S_{db} Sdb。
观察本文开头图中传统/mini-batch梯度下降的折线,斜率或者说函数的倾斜程度在垂直方向( b b b)特别大,类似下图。

也就是说,微分在垂直方向的要比水平方向的大得多, d b db db 比较大, d W dW dW 比较小。
而 d b db db 比较大,根据公式 S d b S_{db} Sdb 也会比较大; d W dW dW 比较小,那么 S d W S_{dW} SdW也会比较小。
结果就是纵轴( b b b)上的更新要被一个较大的数相除,就能消除摆动,而水平方向( W W W)的更新则被较小的数相除。
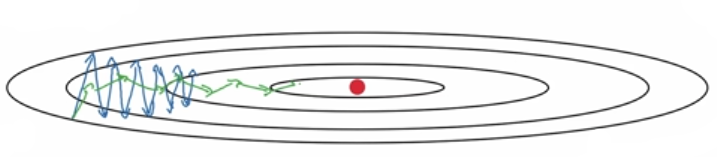
如上图。RMSprop算法梯度下降过程是绿色线,纵轴方向上摆动较小,而横轴方向继续推进。
使用RMSprop算法跟Momentum有很相似的一点,可以消除梯度下降中的摆动,包括mini-batch梯度下降。你可以用一个更大学习率 α \alpha α,加快算法学习速度,而无须在纵轴上垂直方向偏离。
Momentum 和 RMSprop是存在区别的。
前者是在梯度的更新方向上做优化,没有考虑数值大小;后者在数值大小上进行优化,在梯度值较大的方向进行适当的减小步伐,在梯度值较小的方向适当增大步伐,没有考虑方向。
但是两者在优化效果上基本上是一致的,即减小了个别方向上的震动幅度,加快了收敛速度。
要说明一点,这里一直把纵轴和横轴方向分别称为 b b b 和 W W W,只是为了方便展示而已。实际中,你会处于参数的高维度空间。在你要消除摆动的维度中,最终你要计算一个更大的微分平方和的加权平均值(例如 S d b S_{db} Sdb),最后去掉了那些有摆动的方向。
这就是RMSprop,全称是均方根,因为你将微分进行平方,然后最后使用平方根。
为了避免和Momentum算法的超参 β \beta β混淆,我们把RMSprop的超参改为 β 2 \beta_2 β2,公式变为
- S d W = β 2 S d W + ( 1 − β 2 ) d W 2 S_{dW}=\beta_2 S_{dW}+(1-\beta_2) dW^2 SdW=β2SdW+(1−β2)dW2
- S d b = β 2 S d b + ( 1 − β 2 ) d b 2 S_{db}=\beta_2 S_{db}+(1-\beta_2) db^2 Sdb=β2Sdb+(1−β2)db2
有一点请注意,如果 S d W S_{dW} SdW 和 S d b S_{db} Sdb趋近为0,也就是更新W和b时候,分母为0,我们要在分母上加上一个很小很小的数 ϵ \epsilon ϵ,例如 10-8,这只是保证数值能稳定一些。公式变为
- W : = W − α d W S d W + ϵ W := W - \alpha \frac {dW}{\sqrt {S_{dW}}+\epsilon} W:=W−αSdW+ϵdW
- b : = b − α d b S d b + ϵ b := b - \alpha \frac {db}{\sqrt {S_{db}}+\epsilon} b:=b−αSdb+ϵdb
这篇关于2020-6-3 吴恩达-改善深层NN-w2 优化算法(2.7 RMSprop -消除梯度下降中的摆动,加速下降,加快学习 -和动量异同点)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



