【数值计算方法】矩阵特征值与特征向量的计算（一）：Jacobi 旋转法及其Python实现

本文主要是介绍【数值计算方法】矩阵特征值与特征向量的计算（一）：Jacobi 旋转法及其Python实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

  矩阵的特征值（eigenvalue）和特征向量（eigenvector）在很多应用中都具有重要的数学和物理意义。Jacobi 旋转法是一种用于计算对称矩阵特征值和特征向量的迭代方法。

  本文将详细介绍 Jacobi 旋转法的基本原理和步骤，通过一个具体的矩阵示例演示其应用过程，并给出其Python实现。

一、Jacobi 旋转法

  Jacobi 旋转法的每一次迭代中，需要选择一个非对角元素最大的位置，然后构造相应的旋转矩阵，进行相似变换，使得矩阵逐渐对角化。

• 对称矩阵是一个实数矩阵，其转置与自身相等。
• 对于一个方阵$A$，如果存在标量 $\lambda$ 和非零向量 $v$，使得 $Av=\lambda v$，那么 $\lambda$ 就是 $A$ 的特征值，$v$ 就是对应于 $\lambda$ 的特征向量。

1. 基本思想

  Jacobi 旋转法的基本思想是通过一系列的相似变换，逐步将对称矩阵对角化，使得非对角元素趋于零。这个过程中，特征值逐渐浮现在对角线上，而相应的特征向量也被逐步找到。下面是 Jacobi 旋转法的基本步骤：

1. 选择旋转角度： 选择一个旋转角度 θ，通常使得旋转矩阵中的非对角元素为零，从而实现对角化，通常选择非对角元素中绝对值最大的那个作为旋转的目标。

2. 构造旋转矩阵： 构造一个旋转矩阵 J，该矩阵为单位矩阵，只有对应于选择的非对角元素的位置上有两个非零元素，其余位置上为零。这两个非零元素的值由旋转角度 θ 决定，例如，对于 2x2 矩阵，旋转矩阵可以表示为：
   $$J=\left[\begin{array}{cc}\cos (\theta )& -\sin (\theta )\\ \sin (\theta )& \cos (\theta )\end{array}\right]$$

3. 相似变换： 计算相似变换矩阵 $P$，即 $P^{T}AP$，其中 $A$ 是原始矩阵，$P$ 是旋转矩阵，计算过程如下：

$$P^{T}AP={\left[\begin{array}{cc}\cos (\theta )& \sin (\theta )\\ -\sin (\theta )& \cos (\theta )\end{array}\right]}^T\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{12}& a_{22}\end{array}\right]\left[\begin{array}{cc}\cos (\theta )& -\sin (\theta )\\ \sin (\theta )& \cos (\theta )\end{array}\right]$$

  通过矩阵相乘计算，我们可以得到 $P^{T}AP$ 中的非对角元素，假设这两个元素分别位于矩阵的 (1,2) 和 (2,1) 的位置。令 $a_{ij}$ 为这两个元素，即 $a_{ij}=a_{12}=a_{21}$。

  接下来，我们希望通过选择合适的 $\theta$使得 $a_{ij}$ 变为零，从而达到对角化的目的，即$a_{12}=a_{21}$，进一步可推导出

$$\theta =\frac{1}{2}\arctan \left(\frac{2\cdot a_{ij}}{a_{ii}-a_{jj}}\right)$$

• 若$a_{ii}=a_{jj}$，则使用$arccot$形式

4. 迭代： 重复步骤 1-3，直到矩阵 A 的非对角元素都趋于零或满足一定的精度要求。

5. 提取特征值和特征向量： 对角线上的元素即为矩阵 A 的特征值，而 P 中的列向量即为对应于这些特征值的特征向量。

2. 计算过程演示

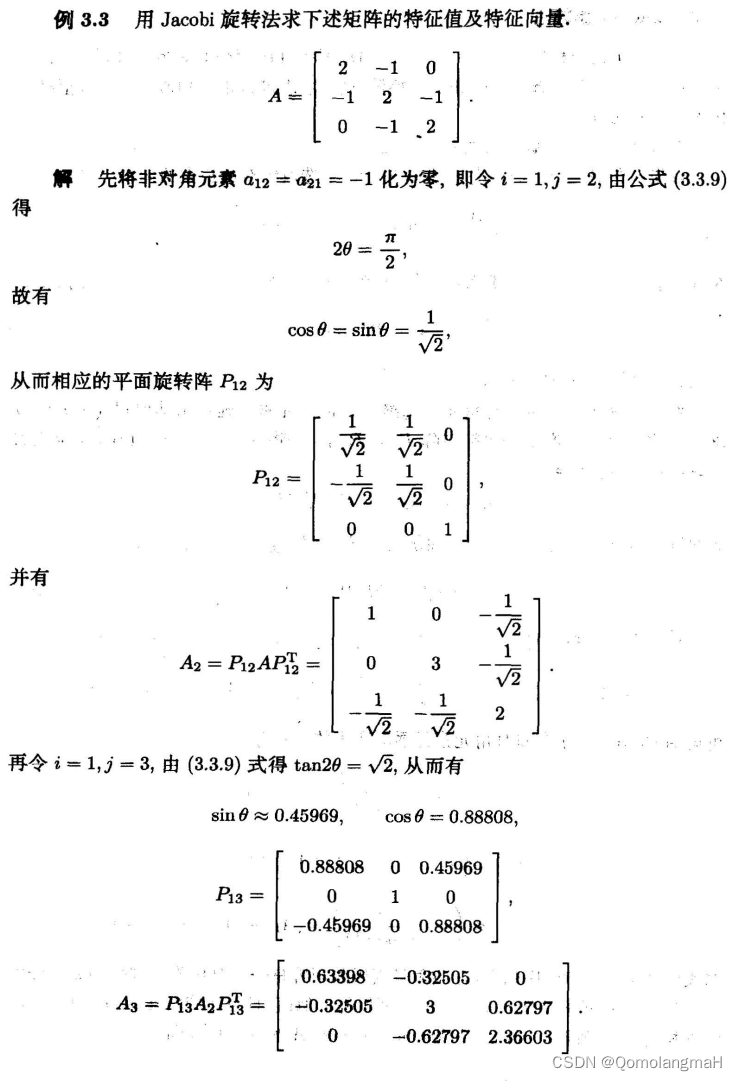
  对于矩阵
$$A=\left[\begin{array}{ccc}2& -1& 0\\ -1& 2& -1\\ 0& -1& 2\end{array}\right]$$

  我们首先找到非对角元素中绝对值最大的元素，这里我们以 (2,1) 为例，计算旋转角度和旋转矩阵。

1. 选择旋转角度：

     计算旋转角度 $\theta$公式：
   $$\theta =\frac{1}{2}\arctan \left(\frac{2\cdot a_{ij}}{a_{ii}-a_{jj}}\right)$$其中，$a_{ii}$和 $a_{jj}$ 分别是矩阵的对角元素，而 $a_{ij}$ 是非对角元素，即 $a_{21}$。 在这个例子中，$a_{21}=-1$，$a_{11}=a_{22}=2$。

   $\theta =\frac{1}{2}\arctan \left(\frac{-2}{0}\right)=-\frac{\pi }{4}$

2. 构造旋转矩阵：

   构造旋转矩阵 ( J )：

$J=\left[\begin{array}{cc}\cos (\theta )& -\sin (\theta )\\ \sin (\theta )& \cos (\theta )\end{array}\right]$

对于 $\theta =-\frac{\pi }{4}$：

$J=\left[\begin{array}{cc}\cos \left(-\frac{\pi }{4}\right)& -\sin \left(-\frac{\pi }{4}\right)\\ \sin \left(-\frac{\pi }{4}\right)& \cos \left(-\frac{\pi }{4}\right)\end{array}\right]$

计算得：

$J=\left[\begin{array}{cc}\frac{\sqrt{2}}{2}& \frac{\sqrt{2}}{2}\\ -\frac{\sqrt{2}}{2}& \frac{\sqrt{2}}{2}\end{array}\right]$

3. 相似变换：

   计算相似变换矩阵 $P$：

   $P^{T}AP$

   在这里，$P$就是构造的旋转矩阵$J$。

4. 迭代：

   重复上述步骤，直到矩阵足够接近对角矩阵。

  这个过程会一步步地使矩阵趋近于对角矩阵，对角线上的元素就是矩阵的特征值，而相应的列向量就是对应的特征向量。由于计算较为繁琐，我在这里只展示了一个迭代的过程。在实际应用中，你需要进行多次迭代，直到满足精度的要求。

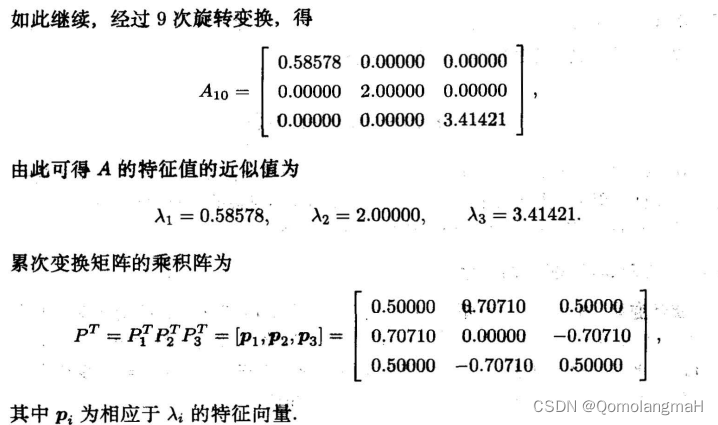
3. 注意事项

  Jacobi 旋转法的优点是可以用于任意大小的对称矩阵，但其缺点是迭代次数较多，计算量较大。在实际应用中，通常会结合其他方法来提高计算效率。

二、Python实现

import numpy as npdef jacobi_rotation(A):n = A.shape[0]tolerance = 1e-10max_iterations = 1000eigenvectors = np.eye(n)for _ in range(max_iterations):# 寻找最大的非对角元素max_off_diag = np.max(np.abs(np.triu(A, k=1)))if max_off_diag < tolerance:break  # 达到收敛条件# 找到最大元素的索引indices = np.unravel_index(np.argmax(np.abs(np.triu(A, k=1))), A.shape)i, j = indices# 计算旋转角度theta = 0.5 * np.arctan2(2 * A[i, j], A[i, i] - A[j, j])# 构造旋转矩阵J = np.eye(n)J[i, i] = J[j, j] = np.cos(theta)J[i, j] = -np.sin(theta)J[j, i] = np.sin(theta)# 执行相似变换A = np.dot(np.dot(J.T, A), J)# 更新特征向量eigenvectors = np.dot(eigenvectors, J)# 提取特征值eigenvalues = np.diag(A)return eigenvalues, eigenvectors# 示例矩阵
A = np.array([[2, -1, 0],[-1, 2, -1],[0, -1, 2]])# 执行 Jacobi 旋转
eigenvalues, eigenvectors = jacobi_rotation(A)print("特征值:", eigenvalues)
print("特征向量:")
np.set_printoptions(precision=4, suppress=True)
print(eigenvectors)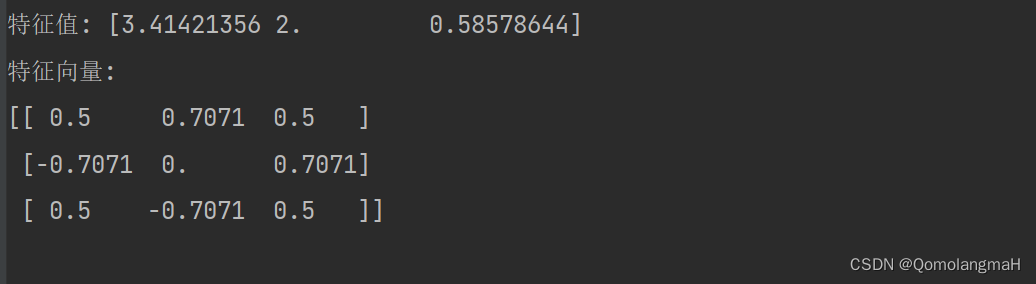

迭代过程（调试）

• 第一次：
  
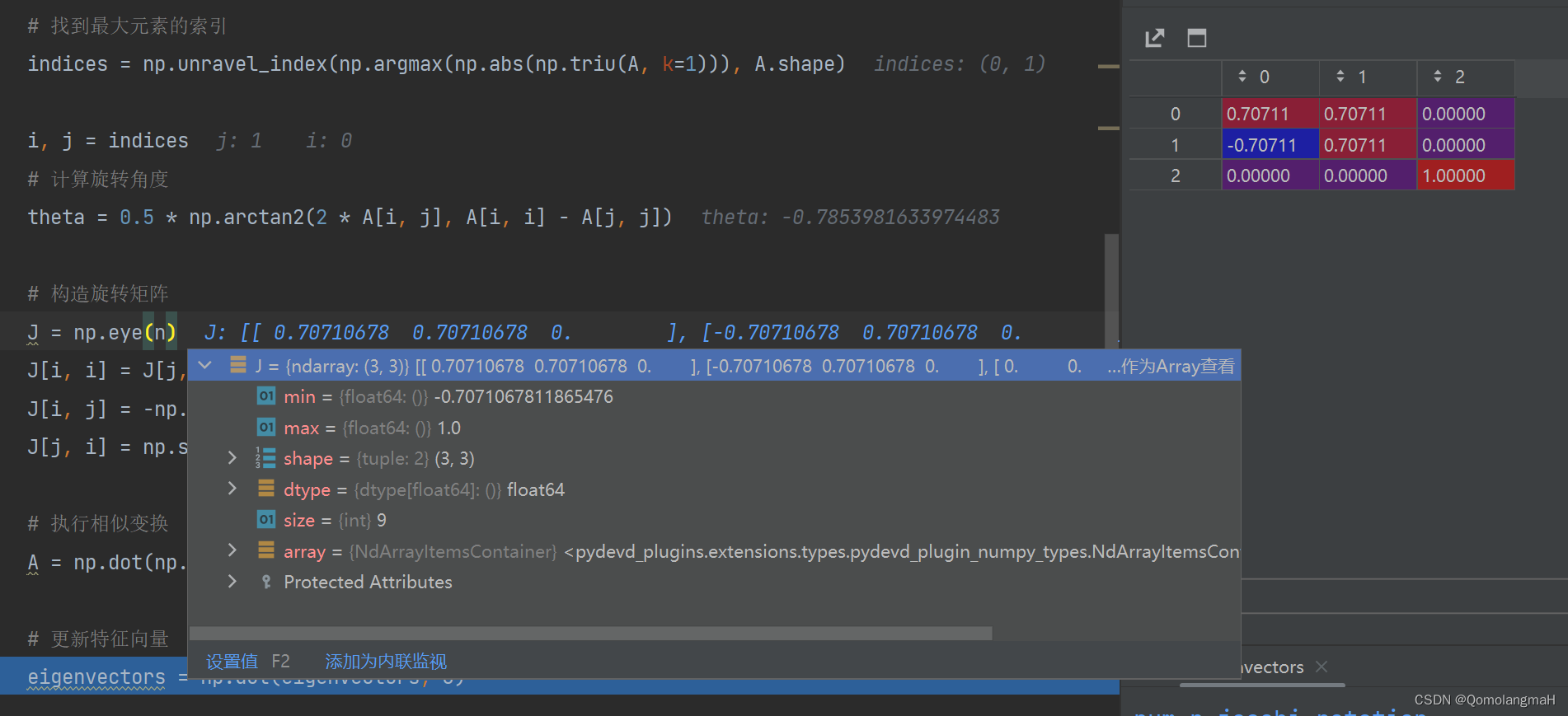
• 第二次：
  ………
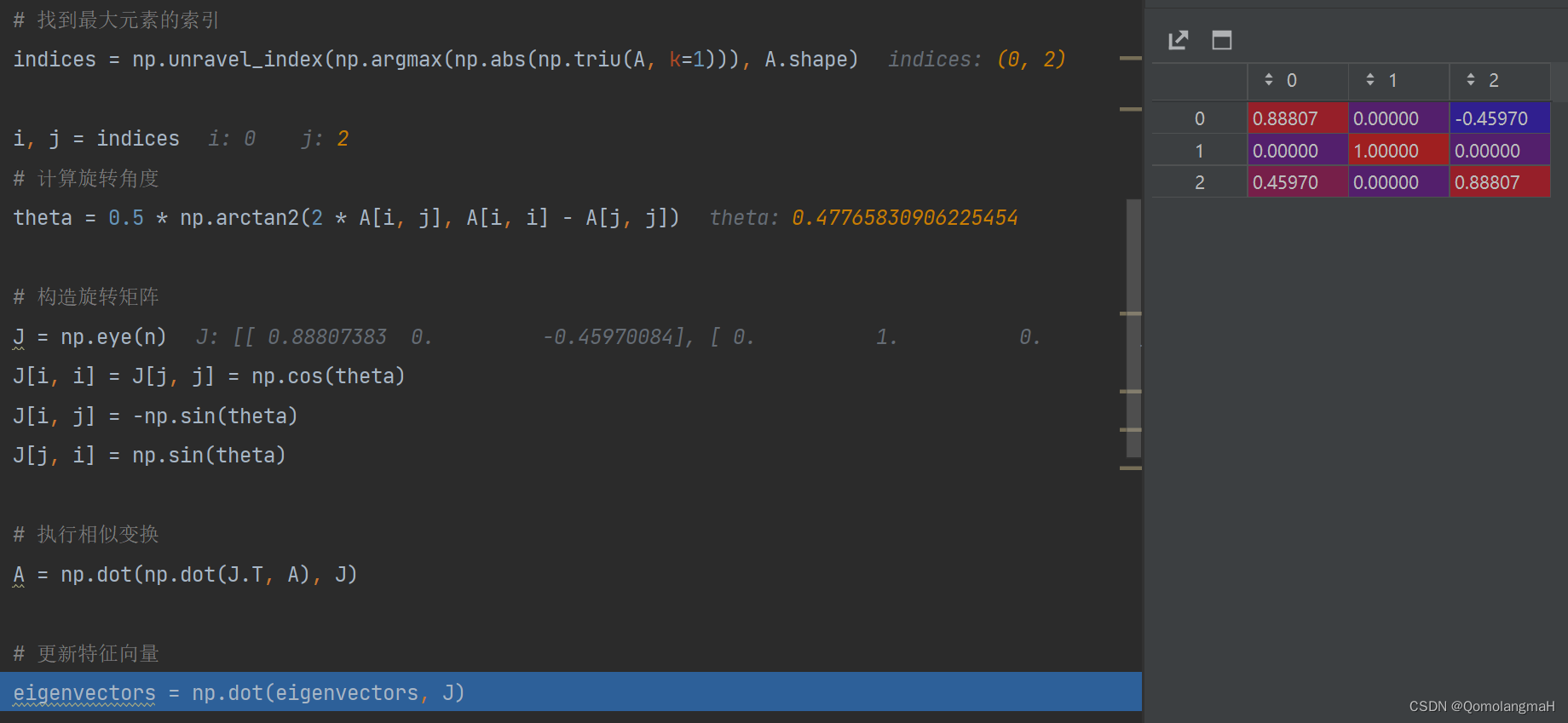
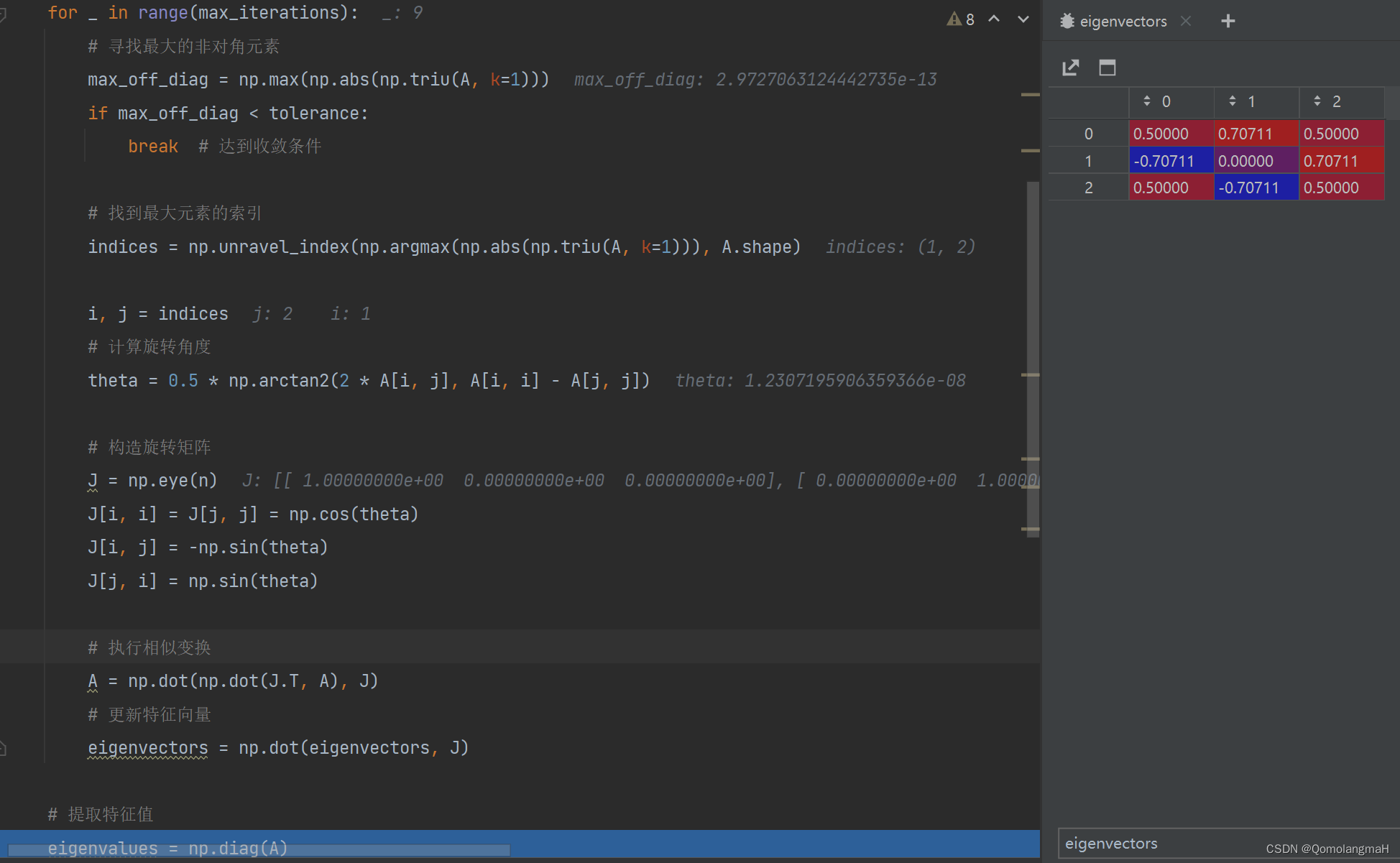
• 第九次：
  

这篇关于【数值计算方法】矩阵特征值与特征向量的计算（一）：Jacobi 旋转法及其Python实现的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---