本文主要是介绍11.20顺序表查找,质数查找,折半查找,任意折查找,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
概念


顺序表查找
int search(int *a,int n, int key){
int i;
a[0]=key;
i=n;
while(a[i]!=key){
i--;}
return i;}就是从数组a的尾部开始找,a是从1开始计数的,所以找到0时,就说明查找失败。


顺序表找最大值
mv=a[1];
for(int i=2;i<=n;i++){if(mv<a[i]){mv=a[i]}
}比较次数n-1 ,无论如何,都要比较n-1
同时找最大最小值
朴素查找
maxv=a[1];
minv=a[1];
for(int i=2;i<=n;i++){if(maxv<a[i]){maxv=a[i];}else if(minv > a[i]){minv=a[i];}
}每次都先和最大值比,再和最小值比,如果比最大值大,那就一定不是最小值,就不需要再和最小值去比较
最好情况为n-1,即升序,每次都是新的最大值,那么每次不需要和最小值比较,每次只和最大值比较即可
最坏情况为2(n-1),即降序 ,每次先和最大值比较,都不比最大值大,那么每次都需要和最小值比,即每个元素都要比两次
快速查找
就是每次取两个,先让取的两个元素比较,就可以比较出一个大的和小的,这时就让大的和此时最大比,小的和最小的比,这样,每两个元素就只需要3次比较次数(一次元素自己比较,两次和最值比较)
相比朴素,朴素每两个要比较四次,每个元素都要和最大最小进行比较,快速就省了一次比较
若每次取三个,就起不到节省的次数,因为此时3个比较,就相当于3个里找最大值最小值,和每个元素直接比较,更加复杂
maxv=a[1],minv=a[1];
k=(n%2)+1;//n为奇数时,k从2开始;n为奇数时,k从1开始
while(k<n){//因为每次循环内都是k和k的下一位,所以k终止条件为n-1,不应该和n取等if(a[k]<a[k+1]){if(min>a[k]){minv=a[k];}if(maxv<a[k+1]){maxv=a[k+1];}}else{if(min>a[k+1]){minv=a[k+1];}if(maxv<a[k]){maxv=a[k];}}k+=2;
}令k=(n%2)+1,n为奇数,如3时,那么从2开始,每次取两个,第一次就能取完,即2,3;如5时,2,3;4,5;
N为偶数,如2时,从1开始,每次取两个,第一次即取1,2 ;如4时,1,2;3,4;
查找区间质数
埃氏筛法

for(int k=2;k<=n;k++){
isp[k]=1;//先假定都是质数
}
for(int k=2;k<=n;k++){//从头开始遍历,2,3一定是质数if(isp[k]=1){//从底层开始,那么没有被标记过的一定是质数m=2*k;//基于找到质数基础上,在后续的序列中,把这个质数的所有倍数都删掉while(m<=n){//一直到越界isp[m]=0;//标记为不是质数m+=k;//每次都增加这个质数的一倍}}
}不是质数的数,都可以被质数唯一表示 ,即每个数,都可以被质数表示

合数限定法
while(!q.empty()){m=q.front();while(m*pk<=n){isp[m*pk]=0;enqueue(M,m);m=m*pk;}
}欧拉筛法

每个数都可以被质数唯一表示,那么每个数一定存在构成其的最小质数,
那么在第一次遍历到那个最小质数时,就一定可以删除掉这个数
相比埃氏筛法,
欧拉筛法中,如果当前数的质数,那么删掉已记录的所有已知质数,直到自己
如果不是质数,那么一直删到自己的最小质因数,比如4,只要2即可;9时,乘2要删一次,乘3要删一次,之后就停止了
也就是说,对于每个数,都是一直删,直到乘数是它的最小质因数
质数的最小质因数是其自身。
折半查找
int bs(s l,int key){int low=0,high=l.lengh-1,mind;while(low<=high){mid=(low+high)/2;if(l.data[mid]==key){return mid;}else if(l.data[mid]>key){high=mid-1;}else{low=mid+1;}}
return -1;}
查找终止的条件是左区间大于右区间

插值查找
中间值可以表述为
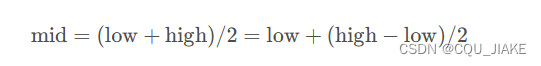
左边意思是区间的中点;右边意思是,左端点加上区间长度的一半;
可改为
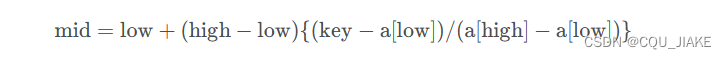
mid=low+(key-l.data[low])/(l.data[high]-l.data[low])*(high-low);这个key就是要查找的值,low是此时区间里最小的值
斐波那契查找
int search(int *a,int n, int key){int low,high,mid,i,k;low=0,high=n,k=0;
这篇关于11.20顺序表查找,质数查找,折半查找,任意折查找的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








