【飞蛾扑火优化算法】基于交叉算子和非均匀变异算子的飞蛾扑火优化算法求解单目标优化问题附matlab代码

1 简介

针对飞蛾扑火优化算法收敛速度慢以及计算后期易收敛到局部最优解的问题,提出了一种基于遗传算法交叉算子和非均匀变异算子的改进方法.该方法在飞蛾围绕火焰飞行的计算过程中,采用交叉算子和变异算子对火焰位置进行扰动以生成新的火焰,当新火焰的适应度值优于原火焰时则替换原火焰,以提高算法的随机性,防止算法过快陷入局部最优解.测试结果表明,改进后的算法在8个常用最优化算法基准测试函数的求解问题中全局收敛能力和收敛速度均优于原算法.

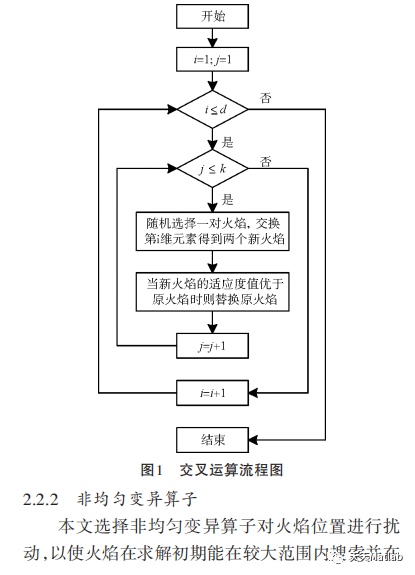
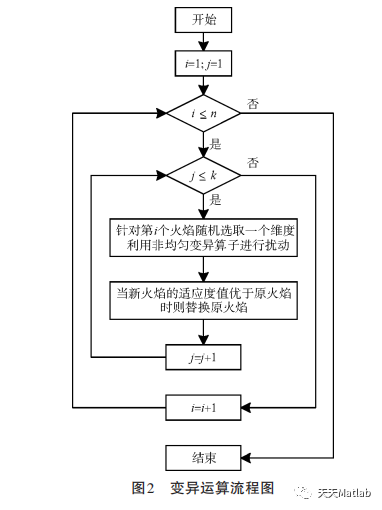
2 部分代码

%______________________________________________________________________________________________%  Moth-Flame Optimization Algorithm (MFO)                                                            %  Source codes demo version 1.0                                                                      %                                                                                                     %  Developed in MATLAB R2011b(7.13)                                                                   %                                                                                                     %  Author and programmer: Seyedali Mirjalili                                                                                                              %                                                                                                     .07.006%_______________________________________________________________________________________________% You can simply define your cost in a seperate file and load its handle to fobj % The initial parameters that you need are:%__________________________________________% fobj = @YourCostFunction% dim = number of your variables% Max_iteration = maximum number of generations% SearchAgents_no = number of search agents% lb=[lb1,lb2,...,lbn] where lbn is the lower bound of variable n% ub=[ub1,ub2,...,ubn] where ubn is the upper bound of variable n% If all the variables have equal lower bound you can just% define lb and ub as two single number numbers​% To run MFO: [Best_score,Best_pos,cg_curve]=MFO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj)%______________________________________________________________________________________________​function [Best_flame_score,Best_flame_pos,Convergence_curve]=MFO(N,Max_iteration,lb,ub,dim,fobj)​display('MFO is optimizing your problem');​%Initialize the positions of mothsMoth_pos=initialization(N,dim,ub,lb);​Convergence_curve=zeros(1,Max_iteration);​Iteration=1;​% Main loopwhile Iteration<Max_iteration+1        % Number of flames Eq. (3.14) in the paper    Flame_no=round(N-Iteration*((N-1)/Max_iteration));        for i=1:size(Moth_pos,1)                % Check if moths go out of the search spaceand bring it back        Flag4ub=Moth_pos(i,:)>ub;        Flag4lb=Moth_pos(i,:)<lb;        Moth_pos(i,:)=(Moth_pos(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;                  % Calculate the fitness of moths        Moth_fitness(1,i)=fobj(Moth_pos(i,:));              end           if Iteration==1        % Sort the first population of moths        [fitness_sorted I]=sort(Moth_fitness);        sorted_population=Moth_pos(I,:);                % Update the flames        best_flames=sorted_population;        best_flame_fitness=fitness_sorted;    else                % Sort the moths        double_population=[previous_population;best_flames];        double_fitness=[previous_fitness best_flame_fitness];                [double_fitness_sorted I]=sort(double_fitness);        double_sorted_population=double_population(I,:);                fitness_sorted=double_fitness_sorted(1:N);        sorted_population=double_sorted_population(1:N,:);                % Update the flames        best_flames=sorted_population;        best_flame_fitness=fitness_sorted;    end        % Update the position best flame obtained so far    Best_flame_score=fitness_sorted(1);    Best_flame_pos=sorted_population(1,:);          previous_population=Moth_pos;    previous_fitness=Moth_fitness;        % a linearly dicreases from -1 to -2 to calculate t in Eq. (3.12)    a=-1+Iteration*((-1)/Max_iteration);        for i=1:size(Moth_pos,1)                for j=1:size(Moth_pos,2)            if i<=Flame_no % Update the position of the moth with respect to its corresponsing flame                                % D in Eq. (3.13)                distance_to_flame=abs(sorted_population(i,j)-Moth_pos(i,j));                b=1;                t=(a-1)*rand+1;                                % Eq. (3.12)                Moth_pos(i,j)=distance_to_flame*exp(b.*t).*cos(t.*2*pi)+sorted_population(i,j);            end                        if i>Flame_no % Upaate the position of the moth with respct to one flame                                % Eq. (3.13)                distance_to_flame=abs(sorted_population(i,j)-Moth_pos(i,j));                b=1;                t=(a-1)*rand+1;                                % Eq. (3.12)                Moth_pos(i,j)=distance_to_flame*exp(b.*t).*cos(t.*2*pi)+sorted_population(Flame_no,j);            end                    end            end        Convergence_curve(Iteration)=Best_flame_score;        % Display the iteration and best optimum obtained so far    if mod(Iteration,50)==0        display(['At iteration ', num2str(Iteration), ' the best fitness is ', num2str(Best_flame_score)]);    end    Iteration=Iteration+1; end​

3 仿真结果

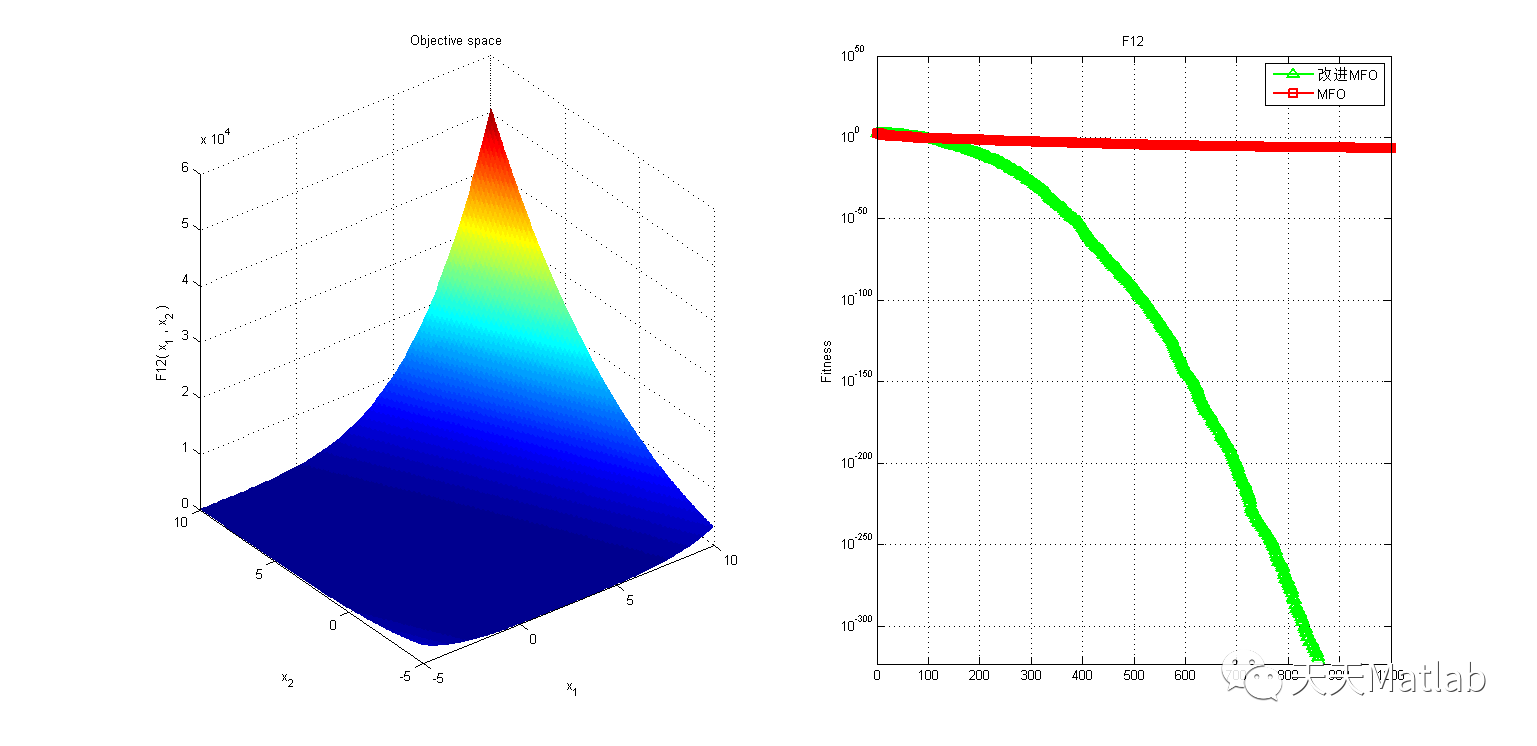
4 参考文献

[1]张保东、张亚楠、郭黎明、江进礼、赵严振. 基于交叉算子和非均匀变异算子的飞蛾扑火优化算法[J]. 计算机与数字工程, 2020, 48(11):6.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。