数值分析：对系数矩阵与向量加扰动后求出解向量

题目

思路

将高斯消去法改写为紧凑形式，可以直接从矩阵A的元素计算出L,U元素的递推公式，因此可以使A分解为L和U。利用LU分解法，求解Ax=b等价于求解Ly=b和Ux=y。
我定义了一个创建希尔伯特矩阵的函数，通过输入行数（列数）来输出一个n阶的希尔伯特矩阵。
为了验证LU分解的正确性，我写了一个矩阵乘积函数，来验证L,U乘积是否等于原来的希尔伯特矩阵。
然后根据题干所给的条件，定义一个创建向量b的函数，以求得b向量的数值。
再根据Ly=b和Ux=y，利用python里面的线性代数计算库scipy-linalg，给出L、b求出y，再给出U、y求出x。

过程

调用hilmat函数，创建希尔伯特矩阵。输出该矩阵。

调用写好了的LU分解函数，求得L,U矩阵。

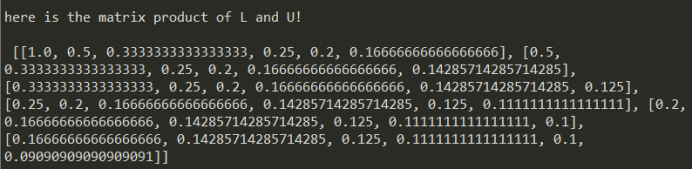
调用矩阵乘积函数，求得L和U的乘积。输出，并与H矩阵比较，数值相同，证明分解成功。

调用创建向量b的函数。创建好向量b后，输出向量b。

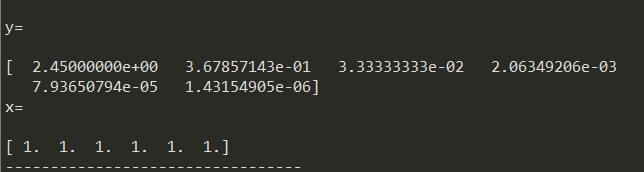
接下来，根据Ly=b，Ux=y，调用linalg.solve函数，先后求得y向量和x向量。

（b）x向量即为希尔伯特矩阵n=6时的解向量。

（c）手动对希尔伯特矩阵做元素的扰动。分四种情况讨论。
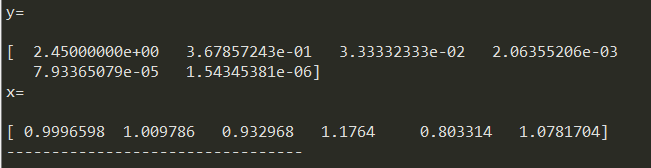
1.a22和a66都增加pow(10,-7)时，解向量如下。

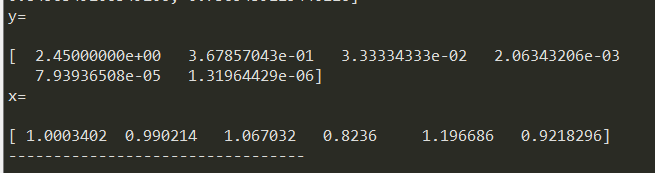
2.a22和a66都减少pow(10,-7)时，解向量如下。

3.a22增加pow(10,-7)，a66减少pow(10,-7)时，解向量如下。

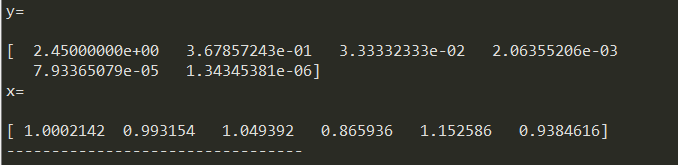
4.a22减少pow(10,-7)，a66增加pow(10,-7)时，解向量如下。

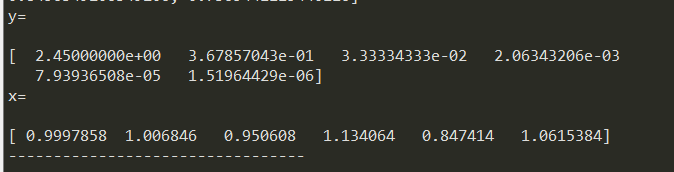
（d）扰动分2种情况。
1.b6增加pow(10,-4)时，解向量如下。

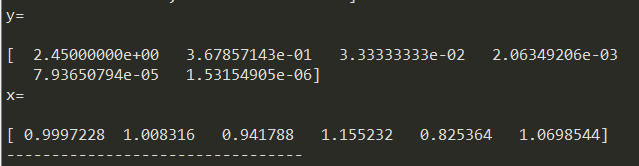
2.b6减少pow(10,-4)时，解向量如下。

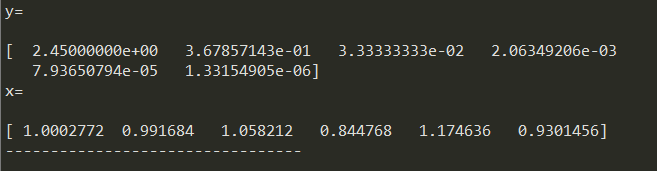
（e）结论：无论是A中元素的扰动，还是向量b元素的扰动，对解向量的值影响都很大。在A改变的元素与b改变的元素在同一个量级，且A元素扰动量级是b元素扰动量级的1/1000的条件下，两种情况造成的解向量的变化范围相当。因此相对而言，A中元素的扰动对解向量的影响更大。

代码

# -*- coding: utf-8 -*-
"""
Created on Wed Jul 15 17:09:33 2020@author: uygfi
"""import numpy as np
import math
from scipy import linalg def matrixMul(A, B):if len(A[0]) == len(B):res = [[0] * len(B[0]) for i in range(len(A))]for i in range(len(A)):for j in range(len(B[0])):for k in range(len(B)):res[i][j] += A[i][k] * B[k][j]return resreturn ('输入矩阵有误！')def hilmat(a):#li=[[]]*ali = [[0] * a for i in range(a)]for i in range(a):for j in range(a):li[i][j]=math.pow((i+j+1),-1)return li#Doolittle分解法np.random.seed(2)
def LU_decomposition(A):n=len(A[0])L = np.zeros([n,n])U = np.zeros([n, n])for i in range(n):L[i][i]=1if i==0:U[0][0] = A[0][0]for j in range(1,n):U[0][j]=A[0][j]L[j][0]=A[j][0]/U[0][0]else:for j in range(i, n):#Utemp=0for k in range(0, i):temp = temp+L[i][k] * U[k][j]U[i][j]=A[i][j]-tempfor j in range(i+1, n):#Ltemp = 0for k in range(0, i ):temp = temp + L[j][k] * U[k][i]L[j][i] = (A[j][i] - temp)/U[i][i]return L,Udef xishu(H):#将b解出来length=len(H[0])V=[0]*lengthfor i in range(0,length):for j in range(0,length):V[i]+=H[i][j]return Vif __name__ == '__main__': H=hilmat(6)print("here is H matrix")print(H)L,U=LU_decomposition(H)print("here is L ,U")print("here is L:\n",L,'\n\n',"here is U:\n",U,'\n')ans=matrixMul(L,U)print(ans,"\n")print("here is the matrix product of L and U!\n\n",H)# LU分解b=xishu(H)print("\n",b,"\n")y = linalg.solve(L, b)print("y=\n")print(y)x = linalg.solve(U, y)print("x=\n")print(x)print("---------------------------------")H[1][1]+=pow(10,-7)H[5][5]+=pow(10,-7)b=xishu(H)print(b)y = linalg.solve(L, b)print("y=\n")print(y)x = linalg.solve(U, y)print("x=\n")print(x)H[1][1]-=pow(10,-7)H[5][5]-=pow(10,-7)print("---------------------------------")H[1][1]-=pow(10,-7)H[5][5]+=pow(10,-7)b=xishu(H)print(b)y = linalg.solve(L, b)print("y=\n")print(y)x = linalg.solve(U, y)print("x=\n")print(x)H[1][1]+=pow(10,-7)H[5][5]-=pow(10,-7)print("---------------------------------")b=xishu(H)b[5]-=pow(10,-7)print(b)y = linalg.solve(L, b)print("y=\n")print(y)x = linalg.solve(U, y)print("x=\n")print(x)b[5]+=pow(10,-7)print("---------------------------------")

参考博客
https://blog.csdn.net/dgq18764215279/article/details/89201238