「算法小记」-2：矩阵链相乘的方案数【迭代/递归/动态规划/区域化DP/记忆化搜索】（C++ ）

本文主要是介绍「算法小记」-2：矩阵链相乘的方案数【迭代/递归/动态规划/区域化DP/记忆化搜索】（C++ ），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

😎 作者介绍：我是程序员洲洲，一个热爱写作的非著名程序员。CSDN全栈优质领域创作者、华为云博客社区云享专家、阿里云博客社区专家博主、前后端开发、人工智能研究生。公粽号：程序员洲洲。
🎈 本文专栏：本文收录于洲洲的《算法小记》系列专栏，该专栏记录了许多常见的各种各样有趣的实战技巧。欢迎大家关注本专栏~专栏一键跳转
🤓 同时欢迎大家关注其他专栏，我将分享Web前后端开发、人工智能、机器学习、深度学习从0到1系列文章。
🌼 同时洲洲已经建立了程序员技术交流群，如果您感兴趣，可以私信我加入我的社群~社群中将不定时分享各类福利
🖥 随时欢迎您跟我沟通，一起交流，一起成长、进步！点此即可获得联系方式~

一、题目描述

题目描述：
设 A1, A2, …, An 为连续相乘的矩阵序列，矩阵相乘满足乘法结合律，那么一共有多少种相乘的方案？

比如 A1, A2, A3, A4 ，通过加括号来体现乘顺序，有 5 种方案：

((A1A2)A3)A4
(A1A2)(A3A4)
A1(A2(A3A4))
(A1(A2A3))A4
A1((A2A3)A4)

输入：
每组数据给出 1 ≤ n ≤ 30。
输出：
n 个矩阵的矩阵链相乘方案数。
输入5，则输出14。
输入10，则输出4862。

解法一：记忆化搜索（区间DP）

#include <iostream>
using namespace std;long long dp[35][35], n;
long long  dfs(int l, int r) {if (l >= r) return 1;if (dp[l][r]) return dp[l][r];for (int mid = l; mid < r; mid++) {dp[l][r] += dfs(l, mid) * dfs(mid + 1, r);}return dp[l][r];
}
int main() {while (cin >> n) {dfs(1, n);cout << dp[1][n] << endl;}return 0;
}

如果说简单的理解这个算法，我们可以打一段输出来检测每一次处理的dp数组的具体数值。

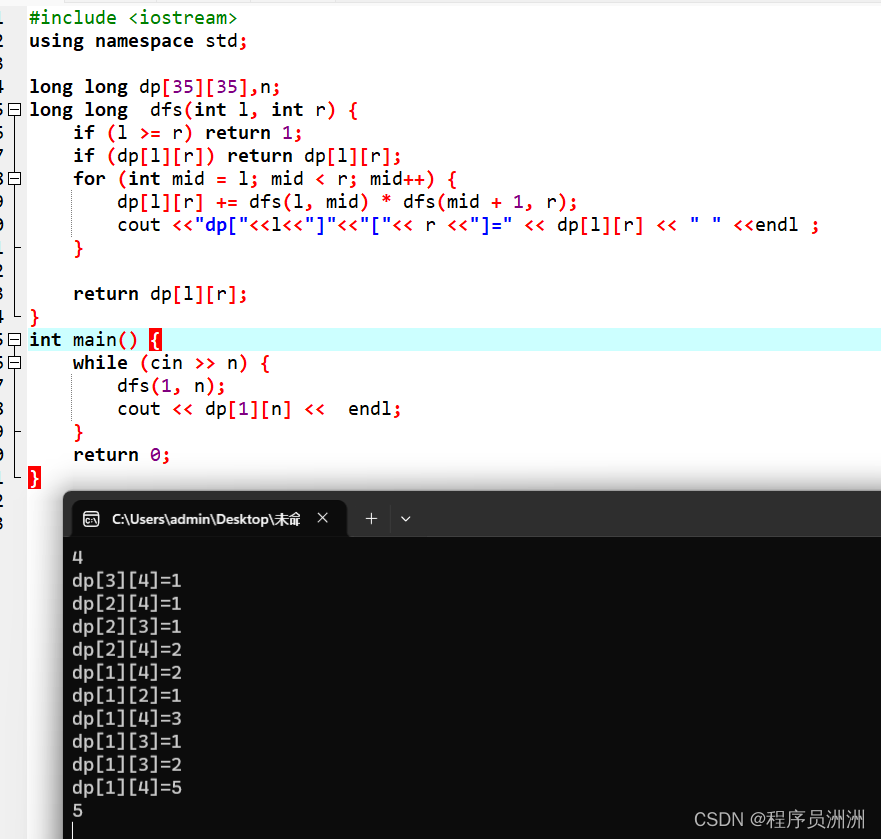
也就是说，当n=4时，可以把问题看成：

14 = 11 * 24 + 12 * 34 + 13 * 44。注意这是一个非常重要的点，有助于我们理解。用dp[i][j]表示区间[i,j]的乘法方案数量，真正的核心点是考虑乘法发生在哪个划分点（切点）。然后不断的去更新这个数量并进行相加。

具体过程可以看成如下：

1. 初始化dp数组：- 创建一个二维数组dp[35][35]，并将所有元素初始化为0。2. 调用dfs(1, 5)：- 进入dfs函数，参数l=1，r=5。3. 判断基本情况：- l=1 小于 r=5，继续执行。4. 判断是否已计算过：- dp[1][5]的值为0（初始值），继续执行。5. 循环遍历分割点：- 初始化mid=l=1。- 进入循环：- mid=1，计算dp[1][5] += dfs(1, 1) * dfs(2, 5)。- 计算dfs(1, 1)：- 进入dfs函数，参数l=1，r=1。- 判断基本情况：l=1 等于 r=1，返回1。- 返回结果1。- 计算dfs(2, 5)：- 进入dfs函数，参数l=2，r=5。- 判断基本情况：l=2 小于 r=5，继续执行。- 判断是否已计算过：dp[2][5]的值为0（初始值），继续执行。- 循环遍历分割点：- 初始化mid=2。- 进入循环：- mid=2，计算dp[2][5] += dfs(2, 2) * dfs(3, 5)。- 计算dfs(2, 2)：- 进入dfs函数，参数l=2，r=2。- 判断基本情况：l=2 等于 r=2，返回1。- 返回结果1。- 计算dfs(3, 5)：- 进入dfs函数，参数l=3，r=5。- 判断基本情况：l=3 小于 r=5，继续执行。- 判断是否已计算过：dp[3][5]的值为0（初始值），继续执行。- 循环遍历分割点：- 初始化mid=3。- 进入循环：- mid=3，计算dp[3][5] += dfs(3, 3) * dfs(4, 5)。- 计算dfs(3, 3)：- 进入dfs函数，参数l=3，r=3。- 判断基本情况：l=3 等于 r=3，返回1。- 返回结果1。- 计算dfs(4, 5)：- 进入dfs函数，参数l=4，r=5。- 判断基本情况：l=4 小于 r=5，继续执行。- 判断是否已计算过：dp[4][5]的值为0（初始值），继续执行。- 循环遍历分割点：- 初始化mid=4。- 进入循环：- mid=4，计算dp[4][5] += dfs(4, 4) * dfs(5, 5)。- 计算dfs(4, 4)：- 进入dfs函数，参数l=4，r=4。- 判断基本情况：l=4 等于 r=4，返回1。- 返回结果1。- 计算dfs(5, 5)：- 进入dfs函数，

解法二：

#include <iostream>
using namespace std;
long long cishu(int n) {long long dp[100][100] = {0};for (int i = 1; i <= n; i++) {dp[i][i] = 1;}for (int len = 2; len <= n; len++) {for (int i = 1; i <= n - len + 1; i++) {int j = i + len - 1;dp[i][j] = 0;for (int k = i; k < j; k++) {//用dp[i][j] 表示区间[i,j]的乘法方案数，考虑最后一次乘法发生在哪里来划分子问题 dp[i][j] = dp[i][j] + (dp[i][k] * dp[k + 1][j]);}}}return dp[1][n];
}
int main() {int n;while(cin >> n){long long num = cishu(n);cout << num << endl;}
}

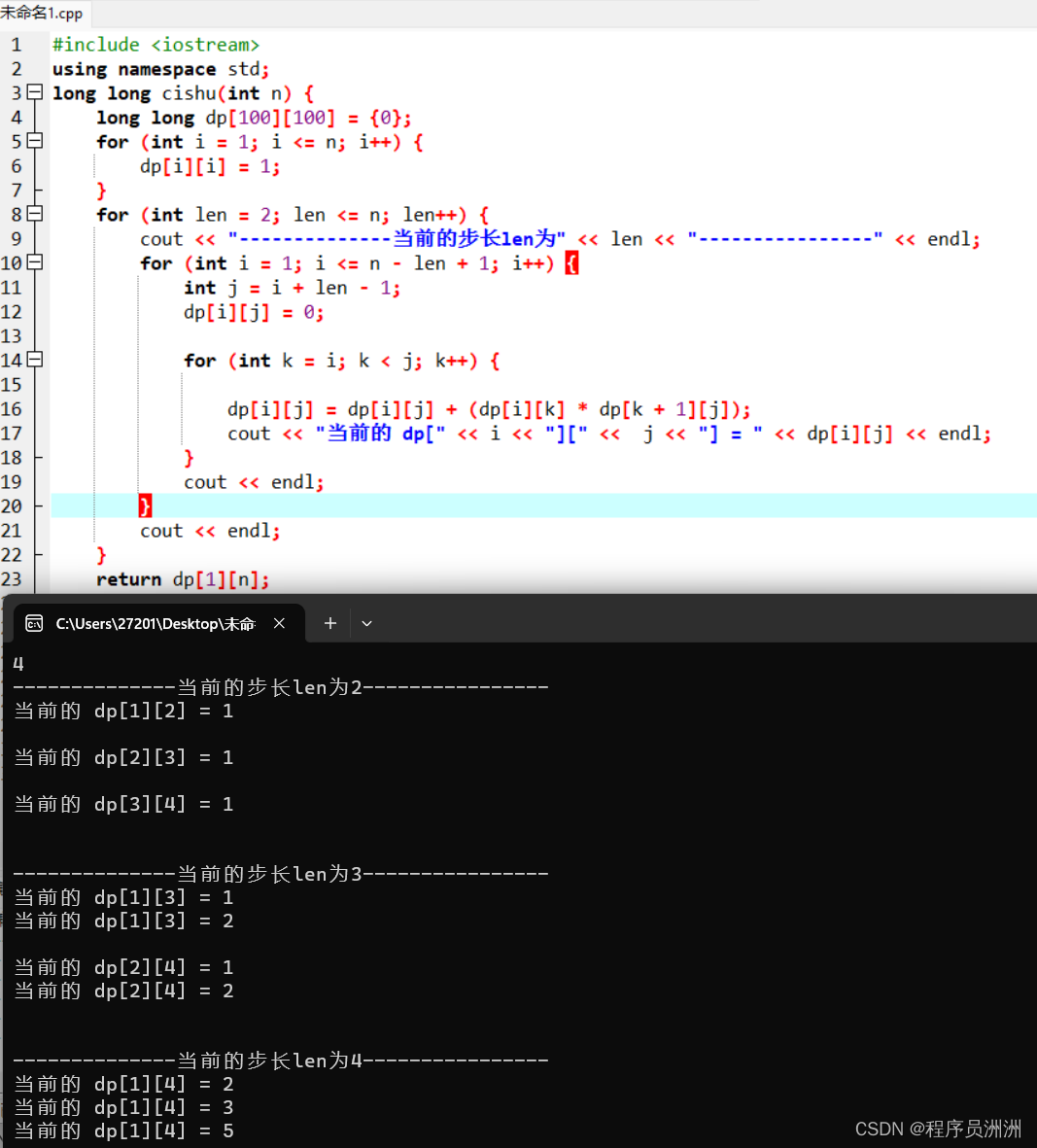
迭代的思想有点难以理解，如果想弄明白的话，建议各位读者手推一遍算法过程。

总结

Hello，各位看官老爷们好，洲洲已经建立了CSDN技术交流群，如果你很感兴趣，可以私信我加入我的社群。

📝社群中不定时会有很多活动，例如每周都会包邮免费送一些技术书籍及精美礼品、学习资料分享、大厂面经分享、技术讨论、行业大佬创业杂谈等等。

📝社群方向很多，相关领域有Web全栈（前后端）、人工智能、机器学习、自媒体变现、前沿科技文章分享、论文精读等等。

📝不管你是多新手的小白，都欢迎你加入社群中讨论、聊天、分享，加速助力你成为下一个技术大佬！也随时欢迎您跟我沟通，一起交流，一起成长。变现、进步、技术、资料、项目、你想要的这里都会有

📝网络的风口只会越来越大，风浪越大，鱼越贵！欢迎您加入社群~一个人可以或许可以走的很快，但一群人将走的更远！

📝关注我的公众号（与CSDN同ID：程序员洲洲）可以获得一份Java 10万字面试宝典及相关资料！~

📝想都是问题，做都是答案！行动起来吧！欢迎评论区or后台与我沟通交流，也欢迎您点击下方的链接直接加入到我的交流社群！~ 跳转链接社区~

这篇关于「算法小记」-2：矩阵链相乘的方案数【迭代/递归/动态规划/区域化DP/记忆化搜索】（C++ ）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---