【优化求解】人工蜂群ABC算法matlab代码

本文主要是介绍【优化求解】人工蜂群ABC算法matlab代码，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab仿真内容点击👇

智能优化算法神经网络预测雷达通信无线传感器电力系统

信号处理图像处理路径规划元胞自动机无人机

⛄ 内容介绍

一、人工蜂群算法的介绍

人工蜂群算法(Artificial Bee Colony, ABC)是由Karaboga于2005年提出的一种新颖的基于群智能的全局优化算法，其直观背景来源于蜂群的采蜜行为，蜜蜂根据各自的分工进行不同的活动，并实现蜂群信息的共享和交流，从而找到问题的最优解。人工蜂群算法属于群智能算法的一种。

二、人工蜂群算法的原理

1、原理

标准的ABC算法通过模拟实际蜜蜂的采蜜机制将人工蜂群分为3类: 采蜜蜂、观察蜂和侦察蜂。整个蜂群的目标是寻找花蜜量最大的蜜源。在标准的ABC算法中，采蜜蜂利用先前的蜜源信息寻找新的蜜源并与观察蜂分享蜜源信息；观察蜂在蜂房中等待并依据采蜜蜂分享的信息寻找新的蜜源；侦查蜂的任务是寻找一个新的有价值的蜜源，它们在蜂房附近随机地寻找蜜源。

假设问题的解空间是D维的，采蜜蜂与观察蜂的个数都是SN，采蜜蜂的个数或观察蜂的个数与蜜源的数量相等。则标准的ABC算法将优化问题的求解过程看成是在D维搜索空间中进行搜索。每个蜜源的位置代表问题的一个可能解，蜜源的花蜜量对应于相应的解的适应度。一个采蜜蜂与一个蜜源是相对应的。与第i个蜜源相对应的采蜜蜂依据如下公式寻找新的蜜源：

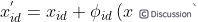
其中，，，，是区间上的随机数，。标准的ABC算法将新生成的可能解与原来的解作比较，并采用贪婪选择策略保留较好的解。每一个观察蜂依据概率选择一个蜜源，概率公式为

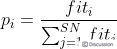
其中，是可能解的适应值。对于被选择的蜜源，观察蜂根据上面概率公式搜寻新的可能解。当所有的采蜜蜂和观察蜂都搜索完整个搜索空间时，如果一个蜜源的适应值在给定的步骤内(定义为控制参数“limit”) 没有被提高, 则丢弃该蜜源，而与该蜜源相对应的采蜜蜂变成侦查蜂，侦查蜂通过已下公式搜索新的可能解。

其中，是区间上的随机数，和是第维的下界和上界。

2、流程

初始化；
重复以下过程：
- 将采蜜蜂与蜜源一一对应，根据上面第一个公式更新蜜源信息，同时确定蜜源的花蜜量；
- 观察蜂根据采蜜蜂所提供的信息采用一定的选择策略选择蜜源，根据第一个公式更新蜜源信息，同时确定蜜源的花蜜量；
- 确定侦查蜂，并根据第三个公式寻找新的蜜源；
- 记忆迄今为止最好的蜜源；
判断终止条件是否成立；

三、人工蜂群算法用于求解函数优化问题

对于函数

其中。

%% Copyright (c) 2015, Yarpiz (www.yarpiz.com)% All rights reserved. Please read the "license.txt" for license terms.%% Project Code: YPEA114% Project Title: Implementation of Artificial Bee Colony in MATLAB% Publisher: Yarpiz (www.yarpiz.com)% % Developer: S. Mostapha Kalami Heris (Member of Yarpiz Team)% % Contact Info: sm.kalami@gmail.com, info@yarpiz.com%clc;clear;close all;%% Problem DefinitionCostFunction=@(x) Sphere(x); % Cost FunctionnVar=5; % Number of Decision VariablesVarSize=[1 nVar]; % Decision Variables Matrix SizeVarMin=-10; % Decision Variables Lower BoundVarMax= 10; % Decision Variables Upper Bound%% ABC SettingsMaxIt=200; % Maximum Number of IterationsnPop=100; % Population Size (Colony Size)nOnlooker=nPop; % Number of Onlooker BeesL=round(0.6*nVar*nPop); % Abandonment Limit Parameter (Trial Limit)a=1; % Acceleration Coefficient Upper Bound%% Initialization% Empty Bee Structureempty_bee.Position=[];empty_bee.Cost=[];% Initialize Population Arraypop=repmat(empty_bee,nPop,1);% Initialize Best Solution Ever FoundBestSol.Cost=inf;% Create Initial Populationfor i=1:nPop pop(i).Position=unifrnd(VarMin,VarMax,VarSize); pop(i).Cost=CostFunction(pop(i).Position); if pop(i).Cost<=BestSol.Cost BestSol=pop(i); endend% Abandonment CounterC=zeros(nPop,1);% Array to Hold Best Cost ValuesBestCost=zeros(MaxIt,1);%% ABC Main Loopfor it=1:MaxIt % Recruited Bees for i=1:nPop % Choose k randomly, not equal to i K=[1:i-1 i+1:nPop]; k=K(randi([1 numel(K)])); % Define Acceleration Coeff. phi=a*unifrnd(-1,+1,VarSize); % New Bee Position newbee.Position=pop(i).Position+phi.*(pop(i).Position-pop(k).Position); % Evaluation newbee.Cost=CostFunction(newbee.Position); % Comparision if newbee.Cost<=pop(i).Cost pop(i)=newbee; else C(i)=C(i)+1; end end % Calculate Fitness Values and Selection Probabilities F=zeros(nPop,1); MeanCost = mean([pop.Cost]); for i=1:nPop F(i) = exp(-pop(i).Cost/MeanCost); % Convert Cost to Fitness end P=F/sum(F); % Onlooker Bees for m=1:nOnlooker % Select Source Site i=RouletteWheelSelection(P); % Choose k randomly, not equal to i K=[1:i-1 i+1:nPop]; k=K(randi([1 numel(K)])); % Define Acceleration Coeff. phi=a*unifrnd(-1,+1,VarSize); % New Bee Position newbee.Position=pop(i).Position+phi.*(pop(i).Position-pop(k).Position); % Evaluation newbee.Cost=CostFunction(newbee.Position); % Comparision if newbee.Cost<=pop(i).Cost pop(i)=newbee; else C(i)=C(i)+1; end end % Scout Bees for i=1:nPop if C(i)>=L pop(i).Position=unifrnd(VarMin,VarMax,VarSize); pop(i).Cost=CostFunction(pop(i).Position); C(i)=0; end end % Update Best Solution Ever Found for i=1:nPop if pop(i).Cost<=BestSol.Cost BestSol=pop(i); end end % Store Best Cost Ever Found BestCost(it)=BestSol.Cost; % Display Iteration Information disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCost(it))]); end %% Resultsfigure;%plot(BestCost,'LineWidth',2);semilogy(BestCost,'LineWidth',2);xlabel('Iteration');ylabel('Best Cost');grid on;

function [SX0]=observe(Q,Lmin,Lmax)%生成的S1为 population行*C列%但是要保证生成的阈值第一个比后一个小，且不能为图像的最大、小灰度值global population C;P=zeros(8*C,1);w=[1,2,4,8,16,32,64,128];SX0=zeros(population,C);num=3;flag=1;i=1;ill=0; while i<=population R=rand(8*C,1); P(:,1)=R(:,1)>=(Q(:,1,i).^2); k=1; while k<=C t=(k-1)*8+1; SX0(i,k)=w(1,:)*double(P(t:t+7,1)); temp=1; while (SX0(i,k)<=Lmin || SX0(i,k)>=Lmax || ((k>1) && SX0(i,k)<=SX0(i,k-1))) && (temp<=num) Rt=rand(8,1); P(t:t+7,1)=Rt(:,1)>=(Q(t:t+7,1,i).^2); SX0(i,k)=w(1,:)*double(P(t:t+7,1)); temp=temp+1; end if (temp>num) && (SX0(i,k)<=Lmin || SX0(i,k)>=Lmax || ((k>1) && SX0(i,k)<=SX0(i,k-1))) flag=0; %表示此组数据不合理 ill=ill+1; R=rand(8*C,1); P(:,1)=R(:,1)>=(Q(:,1,i).^2); %有时会出现停滞状态，由于此处的Q的artha==1 k=1; else flag=1; ill=0; k=k+1; end if ill>=3 Q(:,:,i)=ones(8*C,2,1)/sqrt(2); end end %% while k<=C i=i+1; end% % fid = fopen('data.txt', 'wt');% % for j=1:C% % for i=1:population% % % % fprintf(fid, ' %4.0f ',SX0(i,j));% % if i==population% % fprintf(fid, '\n');% % end% % end% % % % fwrite(fid,SX0(:,j),'integer*population');% % % % fwrite(fid,'\n','char');% % % % end% % fclose(fid);

function i=RouletteWheelSelection(P) r=rand; C=cumsum(P); i=find(r<=C,1,'first');end

function z=Sphere(x) z=sum(x.^2);end