本文主要是介绍m在LTE-A系统载波聚合下的资源分配算法的matlab仿真,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1.算法描述
2.仿真效果预览
3.MATLAB核心程序
4.完整MATLAB
1.算法描述
载波聚合即CA,是LTE-A中的关键技术。是为满足用户峰值速率和系统容量提升的要求,增加系统传输带宽的技术,通过CA技术,用户最高上网速率可提升到300Mbps,带来极速上网体验。载波聚合是LTE-A中的关键技术。为了满足单用户峰值速率和系统容量提升的要求,一种最直接的办法就是增加系统传输带宽。因此LTE-Advanced系统引入一项增加传输带宽的技术,也就是CA。CA技术可以将2~5个LTE成员载波聚合在一起,实现最大100MHz的传输带宽。有效提高了上下行传输速率。终端根据自己的能力大小决定最多可以同时利用几个载波进行上下行传输。CA功能可以支持连续或非连续载波聚合,每个载波最大可以使用的资源是110个RB。每个用户在每个载波上使用独立的HARQ实体,每个传输块只能映射到特定的一个载波上。
LTE采用由eNB构成的单层结构,这种结构有利于简化网络和减小延迟,实现低时延、低复杂度和低成本的要求。与3G接入网相比,LTE减少了RNC节点。名义上LTE是对3G的演进,但事实上它对3GPP的整个体系架构作了革命性的改变,逐步趋近于典型的IP宽带网络结构。
LTE的架构也叫E-UTRAN架构,如图3所示。E-UTRAN主要由eNB构成。同UTRAN网络相比,eNB不仅具有NodeB的功能,还能完成RNC的大部分功能,包括物理层、MAC层、RRC、调度、接入控制、承载控制、接入移动性管理和Inter-cellRRM等。
为了满足LTE-A下行峰速1 Gbps,上行峰速500 Mbps的要求,需要提供最大100 MHz的传输带宽,但由于这么大带宽的连续频谱的稀缺,LTE-A提出了载波聚合的解决方案。
载波聚合(Carrier Aggregation, CA)是将2个或更多的载波单元(Component Carrier, CC)聚合在一起以支持更大的传输带宽(最大为100MHz)。
每个CC的最大带宽为20 MHz。
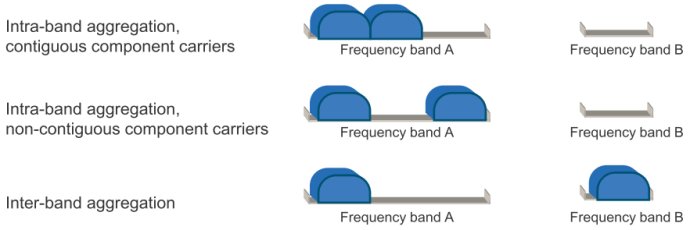
为了高效地利用零碎的频谱,CA支持不同CC之间的聚合(如图1)
· 相同或不同带宽的CCs
· 同一频带内,邻接或非邻接的CCs
· 不同频带内的CCs
从基带(baseband)实现角度来看,这几种情况是没有区别的。这主要影响RF实现的复杂性。
CA的另一个动力来自与对异构网络(heterogeneous network)的支持。后续会在跨承载调度(cross-carrier scheduling)中对异构网络进行介绍。
2.仿真效果预览
matlab2022a仿真结果如下:



3.MATLAB核心程序
for i = 1:length(Nums)iPF_times = 100;%m为调度次数G = Nums(i);%为UE个数CC = 3; %个数T = Twind;Rbs = zeros(G,CC,PF_times); %矩阵s为每次调度RB所分配的UERates = zeros(G,G); %整个调度过程每个UE所获得的速率Avg_rate = ones(1,G,PF_times+1); %每个UE所获得的平均速率Rand_rate= [];Sum_rate = [];%根据用户在CC上的路径损耗进行分组%我们建设CC坐标为,用户坐标随时产生XY1 = [100,200];XY2 = [300,100];XY3 = [200,400];XY = 1000*rand(2,G);SET = [];%定义权重因子L = CC;for j=1:Gdist1 = sqrt((XY(1,j)-XY1(1))^2 + (XY(2,j)-XY1(2))^2); dist2 = sqrt((XY(1,j)-XY2(1))^2 + (XY(2,j)-XY2(2))^2);dist3 = sqrt((XY(1,j)-XY3(1))^2 + (XY(2,j)-XY3(2))^2);dist = [dist1,dist2,dist3];%不同载波频率衰减不一样PL1(j) = 58.83+37.6*log(10*dist1/1e3) + 21*log(10*f1);PL2(j) = 58.83+37.6*log(10*dist2/1e3) + 21*log(10*f2);PL3(j) = 58.83+37.6*log(10*dist3/1e3) + 21*log(10*f3);[V,I] = min([PL1(j),PL2(j),PL3(j)]);SET(j) = I;%分组号Wk(j) = L/G*dist(I)/Avg_rate(1,j,end);distt(j) = min(dist);endWk = Wk/max(Wk);%距离较大的定义为郊区[VV,II] = sort(distt);Ijiq = II(round((1-ker)*G):G);Izx = II(1:round((1-ker)*G)-1);for n=1:PF_times; %调度次数rng(n);%初始化alphaalpha = zeros(1,G);%侵略因子%生成随机速率信息Rand_rate(:,:,n) = randint(G,CC,[0 500]); %pf调度%每个RB开始分配for jq = 1:CC; t = 1;if jq == 1;PL=PL1;end;if jq == 2;PL=PL2;end;if jq == 3;PL=PL3;end;for jG = 2:G; if Rand_rate(jG,jq,n)/Avg_rate(1,jG,n)>Rand_rate(t,jq,n)/Avg_rate(1,t,n) & PL>=300+50*rand;t = jG;endendRbs(t,jq,n) = G*rand;end %获得的速率Sum_rate(:,:,n) = Rbs(:,:,n)*Rand_rate(:,:,n)'; %整个调度过程每个UE所获得的速率Rates(:,:) = Sum_rate(:,:,n)+Rates(:,:); %更新平均速率for k2=1:G; if rand>0.2%得到服务Avg_rate(1,k2,n+1)=(1-1/T).*Avg_rate(1,k2,n); elseAvg_rate(1,k2,n+1)=(1-1/T).*Avg_rate(1,k2,n)+(1/T).*Sum_rate(k2,k2,n);endendendRates_=Wk*Rates;speed1(i) = sum(sum(Rates_(:,Ijiq)))/1e6;speed2(i) = sum(sum(Rates_(:,Izx)))/1e6;speed(i) = speed1(i)+speed2(i);
end
01_181m4.完整MATLAB
V
这篇关于m在LTE-A系统载波聚合下的资源分配算法的matlab仿真的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!